2장 구간 합(Prefix Sum)[PYTHON]

목차
1. 구간 합
2. 그림으로 이해
3. 코드
4. 느낀점

구간 합

구간 합 자체의 개념은 어렵지 않다.
이름 그대로 일정 구간의 합을 나타내는 말이다.
구간 합을 구하고자 하는 데이터를 받았을 때 각 원소를 일일이 합하면 시간 복잡도는 O(N^2)으로 비효율적이다.
하지만 합 배열을 이용하여 구간 합을 다시 구하고자 한다면 시간 복잡도는 O(1)이 된다.
합 배열을 만드는데 걸리는 시간 복잡도는 O(N)이므로 전체적인 시간 복잡도는 O(N)이 된다.
그렇다면 합 배열은 어떻게 만들까?
리스트 num이 존재할 때 합 배열 S와 S를 이용한 구간 합 공식은 아래와 같다.

S[n] = S[n - 1] + num[n] : 합 배열 공식 (n > 0)

S[m] - S[n - 1] : n부터 m까지 구간 합 (n > 0)

그림으로 이해

이제는 그림으로 이해해보자.
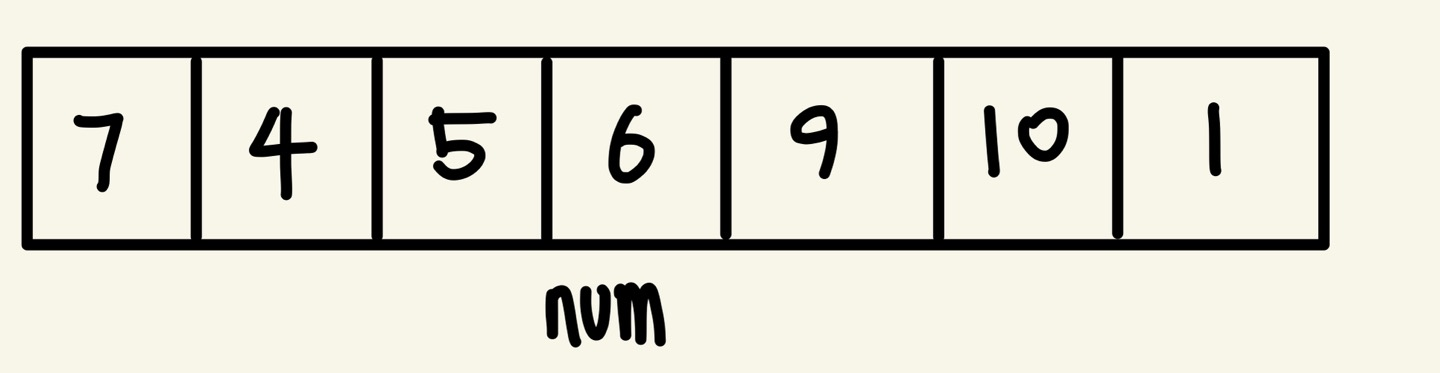
아래와 같이 num 배열이 존재한다고 하자.
우리는 합 배열 SUM을 만들어야 한다.

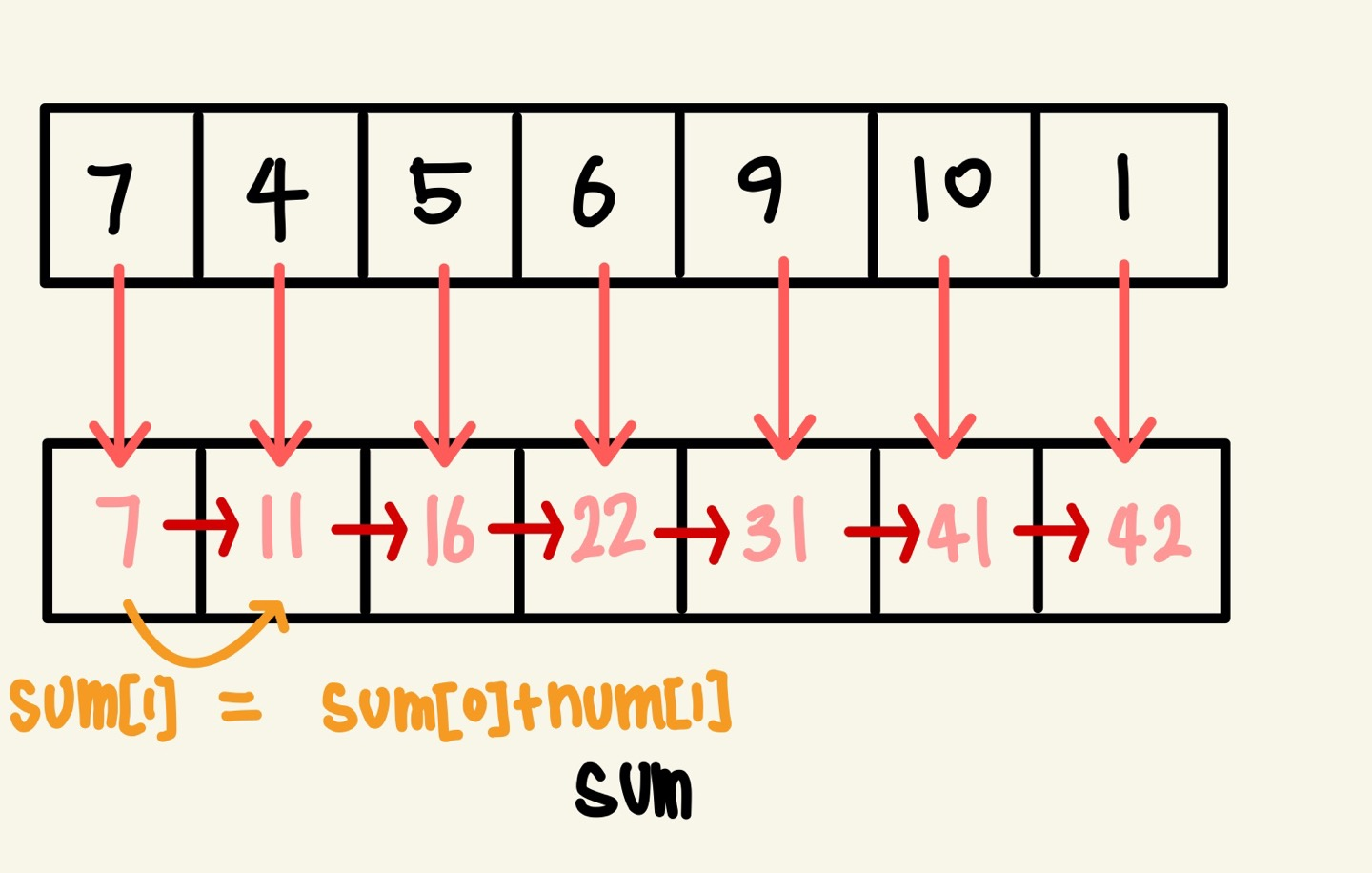
SUM배열을 만드는 과정은 아래와 같다.
첫 번째 원소는 num[0]으로 초기화를 한 후 앞서 말했던 합 매열 공식을 적용하면 된다.
이런 방식을 이용하여 SUM[n] = SUM[n - 1] + num[n] (n > 0)이라는 공식이 나오게 된다.

코드

num = [7, 4, 5, 6, 9, 10, 1]
SUM = []
SUM.append(num[0])

for i in range(1,len(num)):
    SUM.append(SUM[i - 1] + num[i])

print(SUM)

그렇게 어려운 내용이 아니기에 그림과 앞선 설명으로 충분히 이해가 가능 할 것으로 보인다.

느낀점

구간 합이라는 기본적인 알고리즘을 작성하면서 SUM 배열을 이용하여 구간 합을 구하는 과정을 더 잘 이해하게 되었다.