시간 복잡도 (Time Complexity)

들어가기

공학에서 성능은 설계 단계에서 반드시 고려되어야 하는 중요한 요소 중 하나이다. 설계 대상의 성능이 어느 정도로 요구되느냐에 따라서 가능한지 불가능한지, 비용은 어느 정도 예상되는지, 어떻게 설계할 것인지 등등 많은 것들이 결정된다. 그렇다면 코드의 성능을 비교하는 기준은 무엇일까? 컴퓨터 '공학'이므로 성능이라는 추상적인 개념을 명확하게 수치화할 필요가 있다. 알고리즘의 성능을 수치화하기 위해서 사람들이 고민한 결과가 바로 시간 복잡도이다.

---

성능 (Performance)

알고리즘의 성능은 동일한 성과를 도출하기 위해서 요구되는 자원의 크기이다.
동일한 성과를 낸다는 것을 전제하므로 성능은 필요한 자원의 크기를 측정하여 평가한다.

Performance = Solution / Resource

컴퓨터의 자원에는 두 가지가 있다.

공간 복잡도 (Space complexity) : 특정한 프로그램을 수행하는 데 요구되는 메모리
시간 복잡도 (Time complexity) : 특정한 프로그램을 수행하는 데 요구되는 시간

공간 복잡도는 메모리와 관련 있고, 시간 복잡도는 CPU와 관련 있다.
CPU가 훨씬 가격이 비싸고 발전 속도가 느리므로 시간에 대한 자원이 더 중요하다.
따라서 공간 복잡도 보다는 시간 복잡도가 성능 비교에 주로 활용된다.

---

점근적 분석법 (Asymtotic Analysis)

컴퓨터에서의 성능은 아래와 같은 약속(?)이 있다.

1. 성능은 최악의 경우로 측정한다.

항상 최악의 경우만을 기준으로 하는 것은 아니지만, 대체로 그러하다.
최악의 경우를 기준으로하면 어떠한 입력에 대해서도 성능을 보장할 수 있다.

2. 성능은 입력의 크기(n)에 따라 결정된다.

3. 시간 복잡도를 n의 함수로 표현한다. -> $(n,f(n))$

입력되는 자료의 크기가 증가할수록 요구되는 시간의 증가 속도를 표현한다.

4. 점근적 분석법은 매우 큰 입력에 대해서 측정한다. (reasonably large length of input)

작은 입력에 대해서는 의미를 두지 않는다. 성능의 측정은 요구사항을 만족하는지 또는 두 알고리즘을 비교하기 위해서 필요하다. 존재의 이유를 생각해볼 때, 작은 입력에 대해서는 의미를 둘 필요가 없다.

5. worst case $g(n)$을 이용한 $f(n)$의 성능 표현

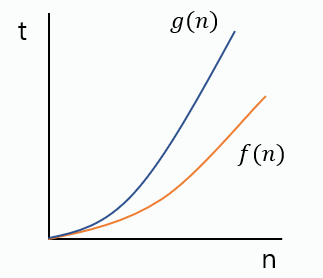
6. worst case $g(n)$은 표준적인 함수를 사용한다.

$\quad 1,\;n,\;n^2,\;\log n,\;n\log n,\;k^n ...$

---

Big-O 표기법 (Big-O notation)

위에 나열된 컴퓨터의 성능에 관한 사항들을 모두 포괄하는 것이 Big-O 표기법이다.

정의

$f(n)\;\,is\;\,O(g(n))\;\,as\;\,n\to \infin,\;\,if\;\,and\;\,only\;\,if\;\,\\ \exists\,n_0,\;\,\exists\,M>0\;\,such\;\,that\;\,f(n)\leq Mg(n)\;\,for\;\,n_0< n$

-> 충분히 큰 $n_0$에 대해서 $f(n)$의 upper bound가 $g(n)$이다.
두 함수 $f(n),\;g(n)$이 $n$에 비례하는 함수 임을 보이기 위해서 상수 $M$이 사용됨.

---

성질

1. 어떤 $n > n_0$에 대해서 $g_1(n) <g_2(n)$이면, $f(n) = O(g_1(n))$은 $f(n) = O(g_2(n))$ 을 의미한다.

ex) $f(n) = O(n)$이면, $f(n) = O(n^2)$

2. 어떤 상수 $k$에 대해서 $f(n) = O(kg(n))$이면, $f(n) = O(g(n))$이다.

ex) $f(n) = O(3n)$이면, $f(n) = O(n)$

3. $f(n) = O(g_1(n)+g_2(n))$이고, $n>n_0$에 대해서 $g_1(n)<g_2(n)$이면, $f(n) = O(g_2(n))$이다.

ex) $f(n) = O(n^2+n)$이면, $f(n) = O(n^2)$

---

예시

1. $f(n)=O(1)$

void func(int n)
{
    printf("Heollo");
}

2. $f(n)=O(n)$

void func(int n)
{
    i = 0;
    while (i < n) {
    	printf("hello");
        ++i;
}

3. $f(n)=O(n^2)$

void func(int n)
{
    for (int i = 0; i < n; ++i) {
    	for (int j = 0; j < n; ++j) {
            printf("hello");
        }
}

4. $f(n)=O(2^n)$

void func(int n)
{
    if (n == 0 || n == 1) return n;
    else return func(n-1) + func(n-2);
}

4. $f(n)=O(\log n)$

void func(int n)
{
    for (int i = 1; i < n; i = i * 10)
    	printf("hello");
}

5. $f(n)=O(n\log n)$

void func(int n)
{
    for (int i = 1; i <= n; ++i) {
    	for (int j = 1; j <= n; j = j * 10) {
    	    printf("hello");
        }
}

크기 비교

$1<\log n<n<n\log n<n^2<k^n$