[알고리즘] 프로그래머스 : 연속 부분 수열 합의 개수 Lv. 2

문제 풀기

문제 설명

철호는 수열을 가지고 놀기 좋아합니다. 어느 날 철호는 어떤 자연수로 이루어진 원형 수열의 연속하는 부분 수열의 합으로 만들 수 있는 수가 모두 몇 가지인지 알아보고 싶어졌습니다. 원형 수열이란 일반적인 수열에서 처음과 끝이 연결된 형태의 수열을 말합니다. 예를 들어 수열 [7, 9, 1, 1, 4] 로 원형 수열을 만들면 다음과 같습니다.

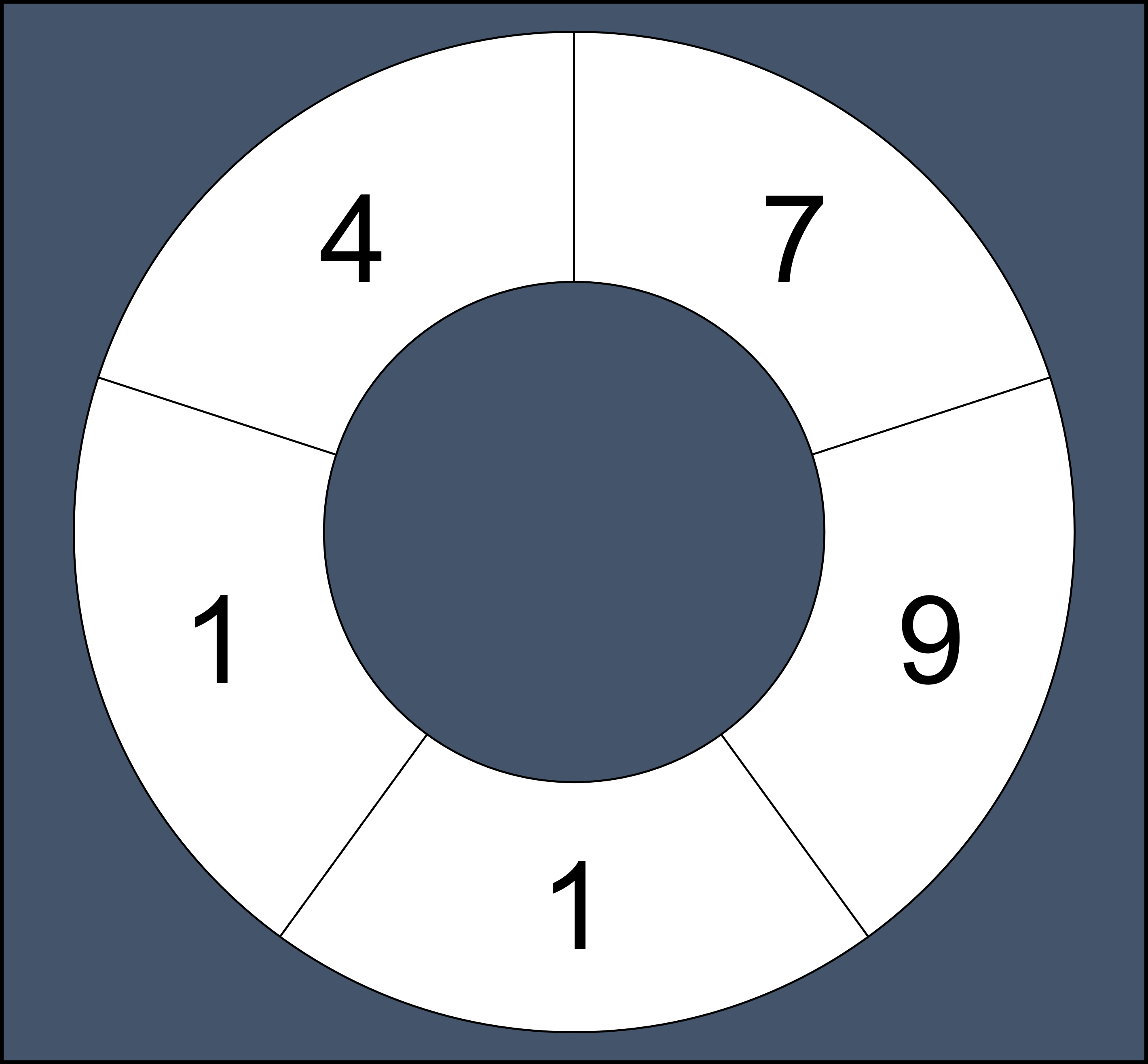
원형 수열은 처음과 끝이 연결되어 끊기는 부분이 없기 때문에 연속하는 부분 수열도 일반적인 수열보다 많아집니다.
원형 수열의 모든 원소 elements가 순서대로 주어질 때, 원형 수열의 연속 부분 수열 합으로 만들 수 있는 수의 개수를 return 하도록 solution 함수를 완성해주세요.

제한사항

• 3 ≤ elements의 길이 ≤ 1,000
• 1 ≤ elements의 원소 ≤ 1,000

입출력 예

elements	result
[7,9,1,1,4]	18

입출력 예 #1

길이가 1인 연속 부분 수열로부터 [1, 4, 7, 9] 네 가지의 합이 나올 수 있습니다.
길이가 2인 연속 부분 수열로부터 [2, 5, 10, 11, 16] 다섯 가지의 합이 나올 수 있습니다.
길이가 3인 연속 부분 수열로부터 [6, 11, 12, 17, 20] 다섯 가지의 합이 나올 수 있습니다.
길이가 4인 연속 부분 수열로부터 [13, 15, 18, 21] 네 가지의 합이 나올 수 있습니다.
길이가 5인 연속 부분 수열로부터 [22] 한 가지의 합이 나올 수 있습니다.
이들 중 중복되는 값을 제외하면 다음과 같은 18가지의 수들을 얻습니다.
[1, 2, 4, 5, 6, 7, 9, 10, 11, 12, 13, 15, 16, 17, 18, 20, 21, 22]

내 정답

import java.util.Set;
import java.util.HashSet;

class Solution {
    public int solution(int[] elements) {
        Set<Integer> answer = new HashSet<>();
        int divisor = elements.length;
        int sum = 0;

        // 현재 위치
        for (int i = 0; i < elements.length; ++i) {
            sum = elements[i];
            answer.add(sum);
            for (int j = i + 1; j % divisor != i; ++j) {
                sum += elements[j % divisor];
                answer.add(sum);
            }
        }

        return answer.size();
    }
}

원리를 설명하자면 아래와 같다

외각 for 루프에서는 sum 에 첫번째 원소를 대입 후 sum 을 set 에 저장한다.
내부 for 루프에서는 sum 에 순차적으로 다음 인덱스를 더한 값을 저장한다.
set 은 중복을 허용하지 않기 때문에 set 의 size를 반환하면 답이 된다.

그러나 위 정답은 중복되는 코드 라인 answer.add(sum) 이 존재하며 속도도 느리다.

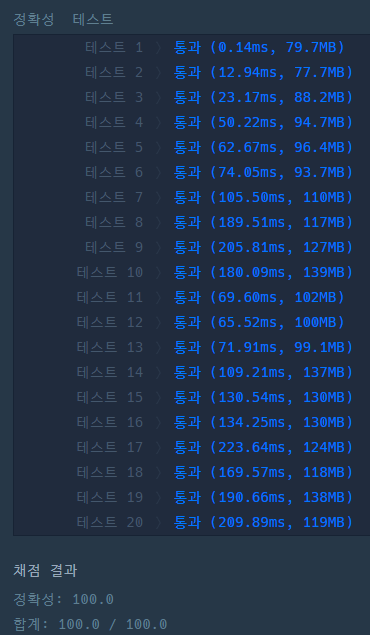
때문에 가장 많은 좋아요를 받은 답은 어떤지 분석해보았다.

가장 많은 좋아요를 받은 답

import java.util.Set;
import java.util.HashSet;

class Solution {
    public int solution(int[] elements) {
        Set<Integer> set = new HashSet<>();
        int[] dp = new int[elements.length];

        for (int len = 1; len <= elements.length; len++) {
            for (int i = 0; i < elements.length; i++) {
                dp[i] += elements[(len + i - 1) % elements.length];
                set.add(dp[i]);
            }
        }
        return set.size();
    }
}

원리를 설명하자면 아래와 같다

외각 for 루프는 변수명을 보면 알 수 있듯 길이를 담당한다.
내부 for 루프는 미리 생성한 배열에 값을 계속 더하며 저장한다.

좀 더 쉽게 아래와 같다.

[1, 4, 7, 9] 가 입력되었다고 가정할 때

[0, 0, 0, 0] : 배열 생성

for 루프 내부
[1, 0, 0, 0] 1 저장
[1, 4, 0, 0] 4 저장
[1, 4, 7, 0] 7 저장
[1, 4, 7, 9] 9 저장
[1 + 4, 4, 7, 9] 5 저장
[1 + 4, 4 + 7, 7, 9] 11 저장
[1 + 4, 4 + 7, 7 + 9, 9] 16 저장
[1 + 4, 4 + 7, 7 + 9, 9 + 1] 10 저장
.
.
.

[21, 21, 21 ,21]

중복이 제거된 set.size() 반환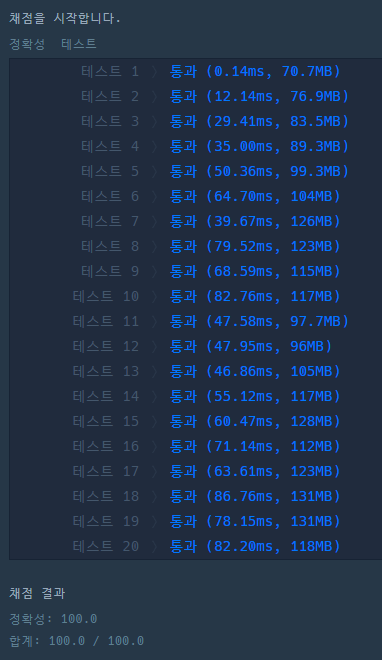

두 자리 ms 를 넘어가지 않으며 훨씬 개선된 속도를 보여준다.

내 정답 개선하기

이에 멈추지 않고 나는 내 정답을 좀 더 수정해보기로 했다.
내 정답을 보면 answer.add(sum) 해당 코드가 두 번 중복된다.
이를 해결하고 싶었으나 방법이 떠오르지 않아 GPT 의 도움을 받았다.

import java.util.Set;
import java.util.HashSet;

class Solution {
    public int solution(int[] elements) {
        Set<Integer> answer = new HashSet<>();

        for (int i = 0; i < elements.length; ++i) {
            int sum = 0;
            for (int j = i; j < i + elements.length; ++j) {
                sum += elements[j % elements.length];
                answer.add(sum);
            }
        }

        return answer.size();
    }
}

이 코드에서 가장 크게 비교되는 부분은 내부의 for 루프 조건식이다.
for (int j = i + 1; j % elements.length != i; ++j) 에서
for (int j = i; j < i + elements.length; ++j) 로 간결하게 바뀌었는데 어떻게 한걸까?

다음과 같다.

내 정답과 내 정답 개선하기의
for 문은 모두 i 인덱스를 기준으로 i 인덱스를 제외한 배열 순회를 의미한다.
동일한 목적을 위해 내부 for 문의 조건문에서 Modulo 연산 대신
ARRAY_LENGTH + 기준 인덱스 i 보다 작은 조건에서 true 이면
기존처럼 sum += elements[j % elements.length] 을 통해 값을 저장할 수 있었다.

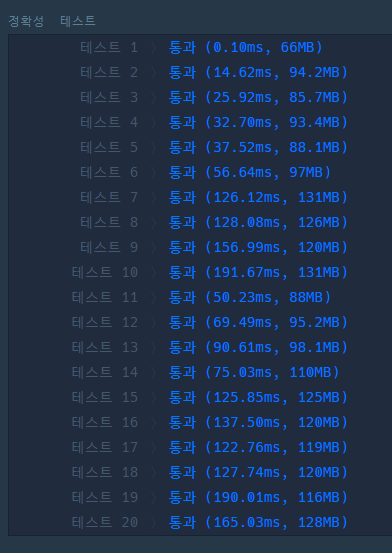
속도도 기존 내 정답은 223ms 까지 느려지는 반면,
GPT 가 수정해준 코드는 최장 시간 192 ms 보다 빠른 것으로 좋아진 것이 눈에 띈다.

그렇다면 여기서 수행시간을 더 줄일 수는 없을까?

import java.util.BitSet;

class Solution {
    public int solution(int[] elements) {
        BitSet answer = new BitSet();

        for (int i = 0; i < elements.length; ++i) {
            int sum = 0;
            for (int j = i; j < i + elements.length; ++j) {
                int element = elements[j % elements.length];
                sum += element;
                answer.set(sum);
            }
        }

        return answer.cardinality();
    }
}

GPT 는 BitSet 을 사용하였다.

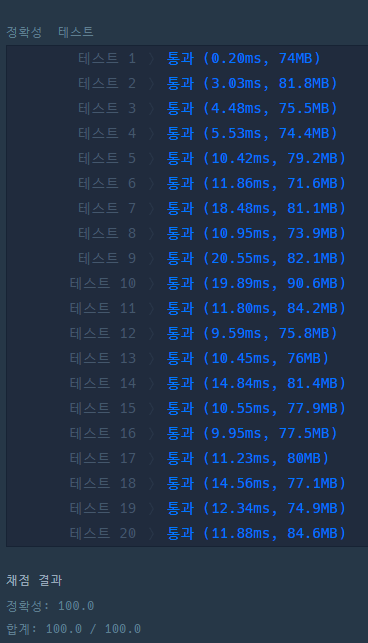
가장 많은 좋아요를 받은 답보다 월등히 빠른 속도를 보여준다.
그렇다면 BitSet 을 가장 많은 좋아요를 받은 답에 적용하면 어떤 결과가 나올까?

import java.util.BitSet;

class Solution {
    public int solution(int[] elements) {
        BitSet answer = new BitSet();
        int[] dp = new int[elements.length];

        for (int len = 1; len <= elements.length; len++) {
            for (int i = 0; i < elements.length; i++) {
                dp[i] += elements[(len + i) % elements.length];
                answer.set(dp[i]);
            }
        }
        return answer.cardinality();
    }
}

획기적으로 빨라진 만큼 눈에 띄는 속도 차이는 발생하지 않는다.

이어서 BitSet 에 대해 포스트를 작성해보겠다.
[자료구조] BitSet