문제
https://programmers.co.kr/learn/courses/30/lessons/72413
접근
1. 다익스트라 (오답)
처음에는 문제를 보자마자 다익스트라가 먼저 떠올랐다. 시작점도 주어졌고, 최소 비용을 구하는 문제였기 때문이다. 과정은 다음과 같았다.
- 다익스트라로 출발점에 대해 나머지 정점으로 가는 최소 비용을 구해놓는다.
- 도착점 a에 대해서 최소 비용을 정답에 더한다.
- 도착점 a가 출발점 s로 가는데 거쳐야 하는 정점들을 저장해놓는다.
- 도착점 b에 대해서 최소 비용을 정답에 더한다.
- 도착점 b가 출발점 s로 가는데 거쳐야 하는 정점들을 조사하는데, 도착점 a -> 출발점 s로 갈 때 중간에 있는 정점 중 최초의 정점을 만났을 때 빠져나온다.
- 도착점 a -> 5번 과정에서 구한 정점 의 비용을 정답에서 빼준다.
이렇게 생각한 이유는 a점과 b점으로 갈 때 각각에 대한 최소 비용이 있을 것이며 공통으로 가는 경로에 대해서는 한 번 빼주면 무조건 정답이라고 생각했기 때문이다.
(택시를 합승하지 않는 경우 각자 마이웨이로 겹치는 경로가 없는 경우라고 생각했다.)
코드
import java.util.*;
class Node implements Comparable<Node>{
int key;
int value;
Node (int key, int value) {
this.key = key;
this.value = value;
}
@Override
public int compareTo(Node n) {
return this.value - n.value;
}
}
class Solution {
public int solution(int n, int s, int a, int b, int[][] fares) {
int answer = 0;
int[] dist = new int[n + 1];
int[] parent = new int[n + 1];
boolean[] visited = new boolean[n + 1];
List<Node>[] graph = new ArrayList[n + 1];
for (int i = 1; i < n + 1; i++) {
graph[i] = new ArrayList<>();
dist[i] = Integer.MAX_VALUE;
parent[i] = i;
}
for (int i = 0; i < fares.length; i++) {
int n1 = fares[i][0];
int n2 = fares[i][1];
int fare = fares[i][2];
graph[n1].add(new Node(n2, fare));
graph[n2].add(new Node(n1, fare));
}
PriorityQueue<Node> pq = new PriorityQueue<>();
pq.add(new Node(s, 0));
dist[s] = 0;
parent[s] = s;
while (!pq.isEmpty()) {
Node node = pq.remove();
int key = node.key;
int value = node.value;
for (int i = 0; i < graph[key].size(); i++) {
Node tmp = graph[key].get(i);
if (value + tmp.value < dist[tmp.key]) {
dist[tmp.key] = value + tmp.value;
parent[tmp.key] = key;
pq.add(new Node(tmp.key, dist[tmp.key]));
}
}
}
int s1 = a;
int s2 = b;
answer += dist[s1]; // 한 명 분량의 택시비 더하기
while (s1 != parent[s1]) {
visited[s1] = true;
s1 = parent[s1];
}
answer += dist[s2];
while (!visited[s2] && s2 != parent[s2]) {
visited[s2] = true;
s2 = parent[s2];
}
System.out.println(s2 + " " + dist[s2]);
if (s2 != s) {
answer -= dist[s2];
}
return answer;
}
}반례
하지만, 저 풀이에 대한 반례가 있었다.
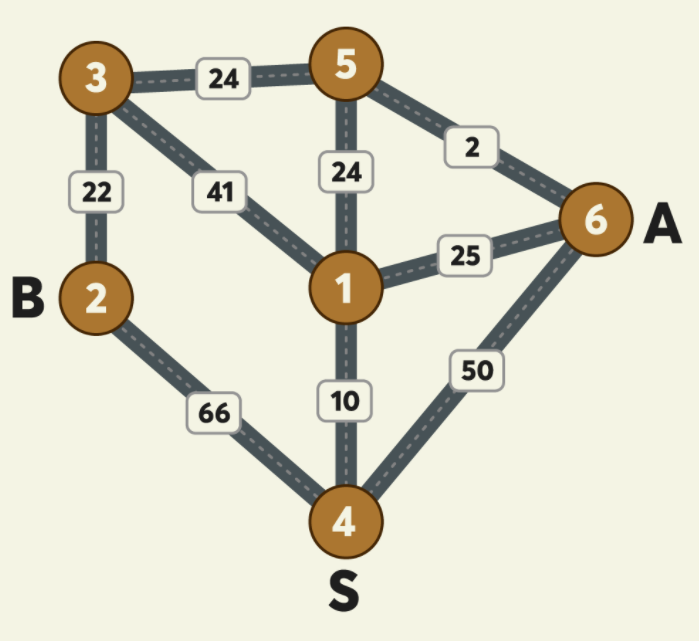
s = 4, a = 2, b = 6
a의 경우 4 -> 1 -> 5 -> 3 -> 2
b의 경우 4 -> 1 -> 5 -> 6
...와 같이 이동해야 한다. 즉, 5번 정점에서 갈라져야 정답이 된다.
하지만, 4번을 출발점으로 다익스트라로 구하게 되면, 6의 경우 최소값이 35 (4 -> 1 -> 6) 이 되고 1번 정점에서 갈라지는 꼴이 된다. 따라서 정답이 아니다.
2. 플로이드 와샬 (정답)
조금만 생각을 바꿔보았을 때, 처음 정점으로부터 최소 비용을 구하는게 아닌, 어느 정점을 출발점으로 두어도 특정 정점으로 갔을 때의 최소 비용이 있으면 될 것 같았다. 그런 알고리즘이 있다는 것은 알았지만 구현 방법을 몰라 이 기회에 플로이드 와샬에 대해 알아보게 되었다.
(플로이드 와샬에 대해서는 추후에 따로 정리하고, 공부할 때 봤던 블로그들을 대신 첨부할 예정이다.)
이를 응용하여 다음과 같은 과정을 생각해봤다.
- 플로이드 와샬 알고리즘을 이용해 각 정점에 대해 최소 비용을 구한다.
- 특정 정점을 t로 두었을 때, t -> a, t ->b, s -> t 에 대한 비용의 합을 구하는 과정을 반복한다.
- 2의 과정 중 최솟값이 정답이 된다.
코드
class Solution {
public int solution(int n, int s, int a, int b, int[][] fares) {
final int MAX = 2000000;
int[][] graph = new int[n + 1][n + 1];
for (int i = 1; i < n + 1; i++) {
for (int j = 1; j < n + 1; j++) {
if (i == j) {
graph[i][j] = 0;
} else {
graph[i][j] = MAX;
}
}
}
for (int i = 0; i < fares.length; i++) {
int n1 = fares[i][0];
int n2 = fares[i][1];
int value = fares[i][2];
graph[n1][n2] = graph[n2][n1] = value;
}
for (int k = 1; k < n + 1; k++) {
for (int i = 1; i < n + 1; i++) {
for (int j = 1; j < n + 1; j++) {
if (graph[i][j] > graph[i][k] + graph[k][j]) {
graph[i][j] = graph[i][k] + graph[k][j];
}
}
}
}
int answer = Integer.MAX_VALUE;
for (int i = 1; i < n + 1; i++) {
if (graph[i][a] == MAX || graph[i][b] == MAX || graph[s][i] == MAX) {
continue;
}
int sum = graph[i][a] + graph[i][b] + graph[s][i];
if (answer > sum) {
answer = sum;
}
}
return answer;
}
}참고 사이트
24. 플로이드 와샬(Floyd Warshall) 알고리즘
[Algorithm] 플로이드 와샬(Floyd-Warshall) 알고리즘