출처: <자바스크립트로 하는 자료구조와 알고리즘>
빅오 표기법: 시공간 복잡도를 나타내는 표기법. 알고리즘의 최악의 경우 복잡도를 측정한다.
빅오 표기법을 통해 실행 시간과 사용된 메모리 관점에서 알고리즘 구현을 분석할 수 있다.
빅오 표기법 기초
빅오 표기법에서 n은 입력의 개수를 나타낸다.
일반적인 빅오 복잡도 예:
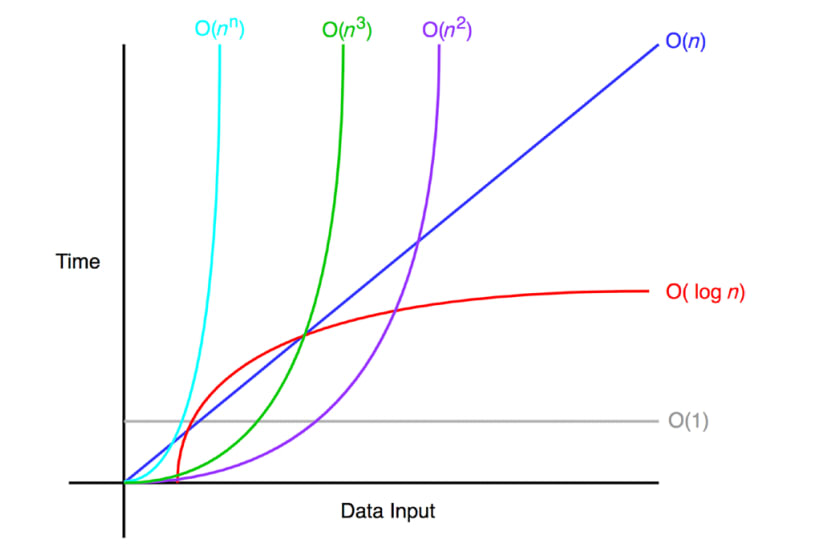
일반적인 예
O(1)은 "상수 시간"이라고 부르며, 입력 공간에 대해 변하지 않는다.
O(1) 알고리즘의 예로는 배열에 있는 요소를 인덱스를 통해 접근하는 경우가 있다.
O(n)은 "선형 시간"이라고 부르며, 최악의 경우에 n번의 연산을 수행해야 하는 알고리즘에 적용된다.
O(n) 알고리즘의 예로는 0부터 n-1까지의 숫자를 출력하는 경우가 있다.
O(n2)는 "2차 시간"이고 O(n3)는 "3차 시간"이다. O(n2) 알고리즘의 예로는 for loop 2개가 nested된 식이 있고, O(n3) 알고리즘의 예로는 for loop 3개가 nested된 식이 있다.
O(log n)은 "로그 시간"이라고 하고, 로그 시간 복잡도를 지닌 알고리즘의 예는 2의 2승부터 n승까지의 항목들을 출력하는 경우가 있다. 예를 들어 exampleLogarithmic(10)은 [2, 4, 8, 16, 32, 64]를 출력한다.
로그 시간 복잡도의 효율은 백만 개처럼 큰 입력이 있는 경우에 분명하다. 이 복잡도를 구현한 코드는 다음과 같다.
function exampleLogarithmic(n) {
for (var i=2; i <= n; i=i*2) {
console.log(i);
}
}빅오 표기법 규칙
알고리즘의 시간 복잡도를 f(n)이라고 표현할 때, n은 입력의 개수를 나타내고, f(n)time은 필요한 시간을 나타내고 f(n)space는 필요한 공간(추가적인 메모리)을 나타낸다. 알고리즘 분석의 목표는 f(n)을 계산함으로써 알고리즘의 효율성을 이해하는 것이다. 그러나 f(n)을 계산하는 것은 어려울 수 있으며, 빅오 표기법은 개발자들이 f(n)을 계산하는 데 도움이 되는 몇 가지 규칙을 제공한다.
- 계수 법칙: 상수 k가 0보다 크다고 할 때(상수 k > 0), f(n)이 O(g(n))이면 kf(n)은 O(g(n))이다. 이는 입력 크기 n과 관련되지 않는 계수를 제거한다. n이 무한에 가까워지는 경우 다른 계수는 무시해도 되기 때문이다.
- 합의 법칙: f(n)이 O(h(n))이고 g(n)이 O(p(n))이면 f(n)+g(n)은 O(h(n)+p(n))이다. 합의 법칙은 결괏값인 시간 복잡도가 두 개의 다른 시간 복잡도의 합이라면 결괏값인 빅오 표기법 역시 두 개의 다른 빅오 표기법의 합이라는 것을 의미한다.
- 곱의 법칙: f(n)이 O(h(n))이고 g(n)이 O(p(n))이면 f(n)g(n)은 O(h(n)p(n))이다. 마찬가지로 곱의 법칙은 두 개의 다른 시간 복잡도를 곱할 때 빅오 표기법 역시 곱해진다는 것을 의미한다.
- 전이 법칙: f(n)이 O(g(n))이고 g(n)이 O(h(n))이면 f(n)은 O(h(n))이다. 교환 법칙은 동일한 시간 복잡도는 동일한 빅오 표기법을 지님을 나타내기 위한 간단한 방법이다.
- 다항 법칙: f(n)이 k차 다항식이면 f(n)은 O(n의 k승)이다. 직관적으로 다항 법칙은 다항 시간 복잡도가 동일한 다항 차수의 빅오 표기법을 지님을 나타낸다.
전이 법칙을 제외한 나머지 4개 법칙은 가장 일반적으로 사용된다.
계수 법칙: "상수를 제거하라"
계수 법칙은 빅오 표기법의 법칙 중 중요도가 제일 높다.
계수 법칙에서는 단순히 입력 크기와 연관되지 않은 상수를 전부 무시하면 된다. (빅오에서 입력 크기가 클 때 계수를 무시할 수 있다.)
상수 k > 0인 경우 f(n)이 O(g(n))이면 kf(n)은 O(g(n))이다.
이는 5f(n)과 f(n)이 모두 동일한 O(f(n))이라는 빅오 표기법을 지님을 의미한다.
시간 복잡도 O(n) 예 1:
// f(n)=n이다. count에 숫자를 n번 더하기 때문이다.
function a(n) {
var count = 0;
for (var i=0; i<n; i++) {
count+=1;
}
return count;
}시간 복잡도 O(n) 예 2:
// f(n)=5n이다. 0부터 5n까지 실행하기 때문이다.
function a(n) {
var count = 0;
for (var i=0; i<5*n; i++) {
count+=1;
}
return count;
}n이 무한대 또는 아주 큰 수에 가까워질 때 네 개의 연산이 추가적으로 존재한다고 해서 달라지는 것은 없기 때문에 위의 두 예 모두 O(n)의 빅오 표기법을 지닌다. "n이 충분히 클 때 위의 코드가 n번 수행된다"고 할 수 있다.
빅오 표기법에서 모든 상수는 무시해도 된다.
시간 복잡도 O(n) 예 3:
선형 시간 복잡도를 지닌 함수이다.
// f(n)=n+1이다. 마지막 연산(count+=3)으로 인해 +1이 추가되었기 때문이다.
function a(n) {
var count = 0;
for (var i=0; i<n; i++) {
count+=1;
}
count+=3;
return count;
}+1이 추가되었지만, 여전히 O(n)의 빅오 표기법이다. 이는 추가된 연산이 입력 n에 영향을 받지 않기 때문이다. n이 무한대에 가까워질수록 추가된 연산은 무시할 수 있게 된다.
합의 법칙: "빅오를 더하라"
합의 법칙은 시간 복잡도를 더할 수 있다는 법칙이다.
두 개의 다른 알고리즘을 포함하는 상위 알고리즘이 있다고 가정했을 때, 해당 상위 알고리즘의 빅오 표기법은 단순히 해당 상위 알고리즘에 포함되는 두 개의 알고리즘의 합이다.
f(n)이 O(h(n))이고 g(n)이 O(p(n))이면 f(n)+g(n)은 O(h(n)+p(n))이다.
합의 법칙을 적용한 다음 계수 법칙을 적용해야 한다는 점에 주의하자.
예 1:
다음 코드는 두 개의 메인 루프를 포함한다. 각 루프의 시간 복잡도는 개별적으로 계산된 다음 더해져야 한다.
function a(n) {
var count = 0;
for (var i=0; i<n; i++) {
count+=1;
}
for (var i=0; i<5*n; i++) {
count+=1;
}
return count;
}첫번째 for loop 내의 식은 f(n)=n에 해당한다. 두번째 for loop 내의 식은 f(n)=5n에 해당한다. 따라서 결과값은 6n이다.
하지만 계수 법칙을 적용하면 최종 결과는 O(n)=n이다.
곱의 법칙: "빅오를 곱하라"
곱의 법칙은 빅오가 어떤 식으로 곱해지는 지에 관한 법칙이다.
f(n)이 O(h(n))이고 g(n)이 O(p(n))이면 f(n)g(n)은 O(h(n)p(n))이다.
예 1:
다음 코드는 두 개의 nested for loop를 포함하며, 이 nested for loop에 곱의 법칙이 적용된다.
function a(n) {
var count = 0;
for (var i=0; i<n; i++) {
count+=1;
for (var i=0; i<5*n; i++) {
count+=1;
}
}
return count;
}위의 예에서 f(n)=5n*n이다. 두번째 for loop 내의 식이 5n번 실행되고, 이 두번째 for loop는 첫번째 for loop에 의해 n번 실행되기 때문이다. 따라서 결과는 5n의 2승만큼 연산이 일어난다.
계수 법칙을 적용하면 결과는 O(n)=n의 2승이 된다.
다항 법칙: "빅오의 k승"
다항 법칙은 다항 시간 복잡도가 동일한 다항 차수를 지닌 빅오 표기법을 지님을 나타낸다.
f(n)이 k차 다항식이면 f(n)은 O(n의 k승)이다.
예 1:
다음 코드에는 2차 시간 복잡도를 지닌 for loop 한 개가 있다.
function a(n) {
var count = 0;
for (var i=0; i<n*n; i++) {
count+=1;
}
return count;
}위의 예에서 f(n)=n의 2승이다. for loop 내의 식이 n*n만큼 실행되기 때문이다.
요약
빅오는 알고리즘의 효율을 분석하고 비교하는 데 중요하다.
빅오를 분석하기 위해서는 코드를 살펴보고 빅오 표기법을 단순화하고자 다음 법칙들을 적용해야 한다. (가장 자주 사용되는 법칙들이다.)
- 계수/상수 제거하기(계수 법칙)
- 빅오 더하기(합의 법칙)
- 빅오 곱하기(곱의 법칙)
- 루프를 조사해 빅오 표기법의 다항 결정하기(다항 법칙)
