프로그래밍 언어의 세계에서 우리는 부동소수점 자료형을 사용하게 된다. 대표적으로 Java, C 등의 float와 double, 그리고 long double이 있다. 이러한 자료형들을 사용할 때에는 연산 할때 오차가 발생할 수 있으니 주의해야 한다.
컴퓨터가 실수를 표현하는 방식을 알아보고, 오차 발생 이유를 알아보도록 한다.
실수 표현 방식
컴퓨터는 모든 수를 0과 1로 이루어진 2진수로 표현한다. 이것은 정수뿐만 아니라 소수점이 존재하는 실수도 마찬가지이다.
정수의 경우 이러한 표현이 간단하지만, 실수를 2진수로 표현하는 것은 복잡하다. 실수를 표현하기 위한 다양한 방법들이 연구되었으며 현재는 크게 2가지 방식이 존재한다.
- 고정 소수점 (fixed point) 방식
- 부동 소수점 (floating point) 방식
고정 소수점 (fixed point) 방식

실수는 보통 정수부와 소수부로 나눌 수 있다. 따라서 실수를 표현하는 가장 간단한 방법은 소수부의 자릿수를 미리 정하고, 고정된 자릿수의 소수를 표현하는 것이다.
- 표현법
정수부 - 2진수 변환 방법 사용
소수부 - 정수부의 반대(2를 곱해가면서 진행), 소수점부터 오른쪽으로 채워서 나머지는 0으로 채운다.
# 10.375 (결과는 위에서 아래로)
0.375 * 2 = 0.75 # 0
0.75 * 2 = 1.5 # 1
0.5 * 2 = 1 # 1
# 10.375 => 1010.011하지만, 이 방식은 정수부와 소수부의 자릿수가 크지 않으므로, 표현할 수 있는 범위가 매우 적다는 단점이 있다. 또한 따라오는 단점으로는 정밀도가 낮다는 특징이 있다. 따라서 높은 정밀도가 필요없는 소규모 시스템에서만 간혹 쓰인다.
부동 소수점 (floating point) 방식
실수는 보통 정수부와 소수부로 나누지만, 가수부와 지수부로 나누어 표현할 수도 있다.
부동 소수점 방식은 실수를 a*2^b 형식으로 저장한다.
이때 a는 1보다 크거나 같고, 2보다 작은 실수이다.
- ±(1.가수부)×2^지수부-127
앞서 살펴본 고정 소수점 방식은 제한된 자릿수로 인해 표현할 수 있는 범위가 매우 작다. 하지만, 부동 소수점 방식은 위의 수식을 이용하여 매우 큰 실수까지도 표현할 수 있다. 그러나 근사값을 저장하기 때문에 정확하지는 않다.
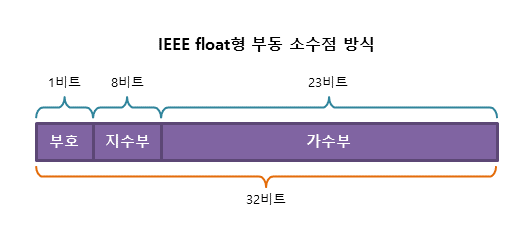

-
표현 방식
대부분 언어에서 4byte float 형식이 32 bit를 따른다.-
단정밀도(Single-Precision)
실수형 중 4byte float 형
32bit(부호-1bit, 지수부-8bit, 가수부-23bit)
지수부가 2^8 = 256개의 수 표현 가능, bias = 127
0~127 구간은 음수를, 128~255 구간은 양수를 표현한다. -
배정밀도(Double-Precision)
실수형 중 8byte double 형
64bit(부호-1bit, 지수부-11bit, 가수부-52bit)
지수부가 2^11 = 2048개의 수 표현 가능, bias = 1023
0~1023 구간은 음수를, 1024~2047 구간은 양수를 표현한다.
4배정밀도 - 128bit(부호-1bit, 지수부-15bit, 가수부-112bit)
-
-
표현법
고정 소수점 방법을 이용하여 변환 후 정수부에 1만 남을 때까지 소수점을 왼쪽으로 이동(정수부가 0일 경우 오른쪽)# 10.375 -> 1010.011 -> 1.010011 * 2^3
# 지수부 : 2, 가수부 : 010011
지수부가 음수일 경우
ex) 2^-10 일 경우 127-10 = 117 -> 1110101
지수부가 양수일 경우
ex) 2^3 일 경우 127+3 = 130 -> 10000010
IEEE 754 표준을 따라 32비트를 사용하는 경우 bias=127을 더해서 사용한다.부동 소수점 방식의 오차
고정 소수점 방식보다 표현 범위가 더 넓지만,
부동 소수점으로 표현하는 실수는 항상 오차가 존재하는 단점을 가지고 있다.
즉, 컴퓨터에서 실수를 표현할 때는 정확한 표현이 아닌 근사치를 표현하는 것이다.
double var = 0.1;
for(int i = 0; i < 1000; i++) {
var += 0.1;
}
System.out.println(var); // 100.09999999.. 가 출력된다.이처럼 컴퓨터에서 실수를 가지고 수행하는 모든 연산에는 언제나 작은 오차가 존재하게 된다. 이것은 자바뿐만 아니라, 모든 프로그래밍 언어에서 발생하는 기본적인 문제이다.
각 자료형의 필요한 정밀도에 따라 유효 자릿수에 맞게 사용해야 한다.
Reference
https://velog.io/@syleemk/CS-%EB%B6%80%EB%8F%99-%EC%86%8C%EC%88%98%EC%A0%90-%EC%98%A4%EC%B0%A8
https://velog.io/@hyungraelee/%EC%8B%A4%EC%88%98%EC%9D%98-%EB%B6%80%EB%8F%99-%EC%86%8C%EC%88%98%EC%A0%90-%EC%A0%80%EC%9E%A5-%EB%B0%A9%EC%8B%9D
https://en.wikipedia.org/wiki/IEEE_754
https://beforb.tistory.com/19
