복잡도 (Complexity)
알고리즘의 성능을 나타내는 지표
-
가독성(Readability)와 다른 의미로 쓰인다.
즉, 코드가 얼마나 복잡하고 알아보기 어려운지를 의미하는 것이 아니라 불특정한 함수의 성능적인 측면에서의 복접도를 의미한다. -
시간 복잡도 : 알고리즘의 수행 시간 분석
-
공간 복잡도 : 알고리즘의 메모리 사용량 분석
-
이때, 동일한 기능을 수행하는 알고리즘이 있다면, 일반적으로 복잡도가 낮은 알고리즘이 좋은 알고리즘이다.
🐰 시간 복잡도 (Time Complexity)
알고리즘이 작업을 완료하는 데 걸리는 시간을 나타낸다.
-
시간 복잡도가 낮다는 말은 알고리즘이 더 빠르고 효율적으로 실행된다는 것을 의미한다.
-
시간 복잡도는 여러가지 개념이 있지만 그중
worst case를 기준으로 표기하는 빅-오(Big-O) 표기법을 사용한다.
즉, 알고리즘이 작업을 완료하는 데 걸리는 최대 시간을 의미한다. -
예를 들어, 시간 복접도가 O(n)인 알고리즘은 입력 크기(n)가 증가함에 따라 실행하는 데 더 오랜 시간이 걸리는 반면, 시간 복잡도가 O(1)인 알고리즘은 입력 크기에 상관없이 실행하는 데 동일한 시간이 걸린다.
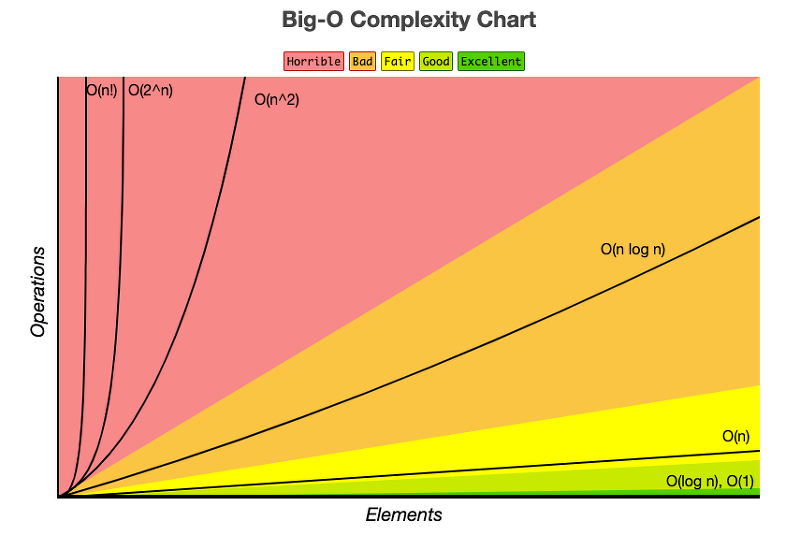
faster O(1) < O(log n) < O(nlog n) < O(n²) < O(2ⁿ) slower
slower로 갈수록(즉, 오른쪽 방향으로 갈수록) 효율성이 떨어진다.
🐰 공간 복잡도 (Space Complexity)
알고리즘이 작업을 완료하는 데 필요한 메모리 양을 나타낸다.
-
공간 복잡도가 낮다는 말은 알고리즘이 더 효율적이고 더 적은 리소스를 사용한다는 것을 의미한다.
-
알고리즘이 입력 크기의 함수로서 요구하는 메모리의 양으로 측정된다.
-
예를 들어, 공간 복잡도가 O(n)인 알고리즘은 입력 크기가 증가함에 따라 더 많은 메모리를 필요로 하는 반면, 공간 복잡도가 O(1)인 알고리즘은 입력 크기에 관계없이 동일한 양의 메모리를 필요로 한다.
정리
- 알고리즘을 설계하고 분석할 때 시간 복잡도와 공간 복잡도 모두 중요한 고려 사항이라는 점에 유의해야 한다.
시간 복잡도가 낮은 알고리즘은 실행하는 데 더 많은 메모리가 필요할 수 있지만 공간 복잡도가 낮은 알고리즘은 실행하는 데 더 오래 걸릴 수 있다. 이 두 요소 사이의 균형은 알고리즘의 특정 요구 사항과 사용 가능한 리소스에 따라 달라진다. 최근에는 하드웨어 메모리 용량이 많이 좋아졌기 때문에 시간 복잡도가 우선시 된다.
