C#_선형보간법(Linear interpolation) 적용

선형보간법이란?

선형 보간법은 1차원 직선상에서 두 점의 값이 주어졌을 때 그 사이의 값을 추정하기 위해 직선 거리에 따라 선형적으로 계산(비례식)하는 방법이다.

---

선형 보간이 필요한 상황

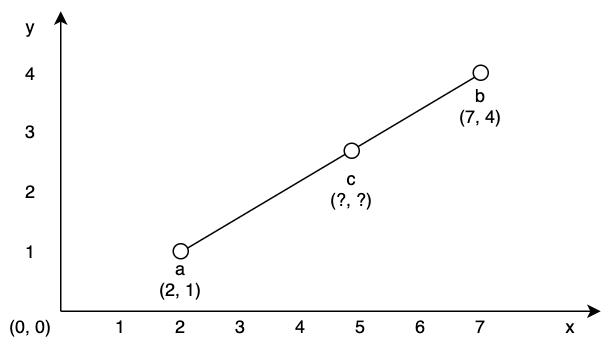
사진을 보면 점 a와 b가 양쪽에 있고, 그 사이에 점 c가 있다. a와 b의 좌표는 각각 (2, 1)와 (7, 4)로 미리 알고있는 상황이며 c는 a와 b사이의 어느 한 지점이라는 점만 알고 있다.
이와 같은 상황에서 점 c의 x좌표가 임의로 주어졌을 때 선형 보간법을 사용하면 점 c의 y좌표까지 알아낼 수 있다.

선형 보간법 적용

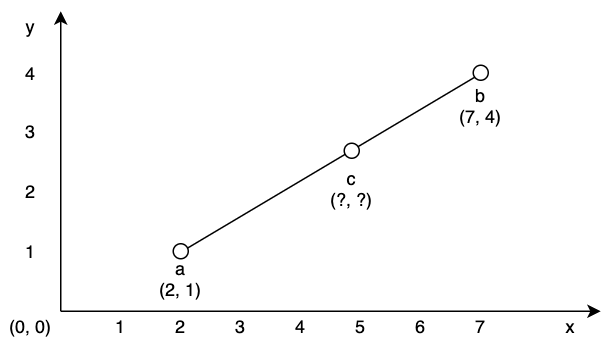
사진을 보면 a와 b가 어느 좌표에 있는지 알 수 있지만 c의 좌표가 어디인지는 확실하게 알 수 없다. 그저 "a와 b 사이의 어딘가" 라는 점만 알 수 있다. 이 때 점 c의 x 좌표를 임의로 지정하면 선형 보간법을 사용하여 점 c의 y 좌표까지 알아낼 수 있다.

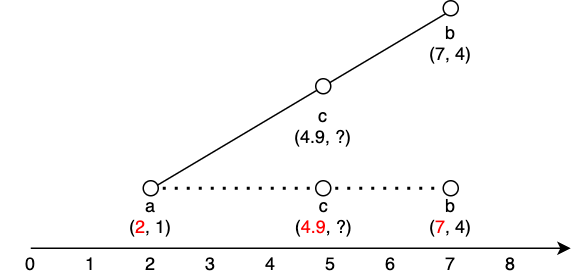
점 c의 x좌표를 4.9로 임의로 정하면 점 a, b, c의 x 좌표(2, 4.9, 7)를 모두 알 수 있는 상태가 된다.
배율 계산을 위해 x 좌표만 가지고 일렬로 늘어뜨려보자. (위 사진에서 실선으로 표시한 부분)

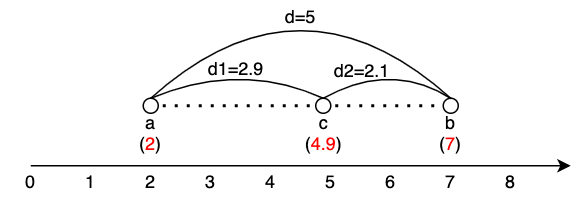
전체거리(d = b - a)를 구하고 시작점과 c 사이의 거리(d1 = c - a)도 구한다. 각각 5, 2.9 라는 숫자가 나오는데 d1에 대한 d의 배율을 구한다.
d1 / d = 2.9 / 5 = 0.58 이므로 백분율로 환산하면 58%을 의미한다.
즉, a로부터 b 방향으로 전체거리(b - a)의 58% 만큼 움직이면 c가 나온다는 뜻이다.

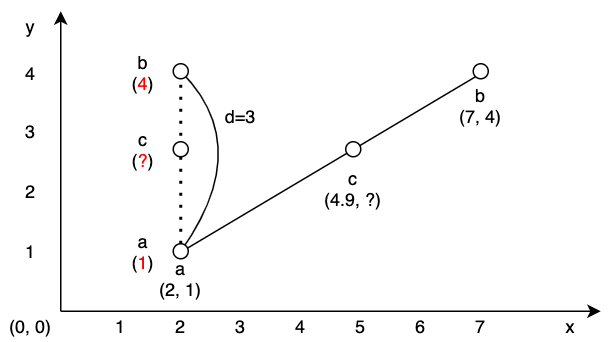
a의 y 좌표와 b의 y 좌표 사이의 거리를 구한 후 위에서 구한 배율을 곱한 뒤 a의 y 좌표를 더하면 c의 y 좌표를 구할 수 있다. 답은 2.74다.

결과적으로 선형 보간법을 사용하면 점 a(2, 1)와 점 b(7, 4) 사이의 점 c의 x 좌표가 4.9 일 때 y 좌표는 2.74 라는 결론을 도출할 수 있다.

출처 : https://spiralmoon.tistory.com/entry/Algorithm-%EC%84%A0%ED%98%95-%EB%B3%B4%EA%B0%84%EB%B2%95-Linear-interpolation

---

C#으로 적용

1. 데이터 생성

double[] x = { 0, 1, 2, 3, 4 };
double[] y = { 1, 3, 5, 7, 9 };

데이터 포인트를 생성한다.

2. 보간 함수 구현

double Interpolate(double[] x, double[] y, double xi)
{
    int i = 0;
    while (i < x.Length && xi > x[i])
    {
        i++;
    }

    if (i == 0 || i == x.Length)
    {
        throw new Exception("xi is out of range");
    }

    double x0 = x[i - 1];
    double x1 = x[i];
    double y0 = y[i - 1];
    double y1 = y[i];

    double yi = y0 + ((xi - x0) / (x1 - x0)) * (y1 - y0);

    return yi;
}

Interpolate 함수는 x와 y 배열, 그리고 보간할 xi 값을 인자로 받는다. 이 함수는 먼저 xi가 x 배열의 범위를 벗어나는지 검사한다. 그리고 xi가 속한 구간의 두 데이터 포인트를 선택하여 일차 함수를 구한다. 이 일차 함수를 이용하여 xi에 대한 예측값 yi를 구하고, 이를 반환한다.

3. 실행

Console.WriteLine(Interpolate(x, y, 2.5)); // 6

4. 전체코드

using System;

namespace LinearInterpolation_Ex
{
    class Program
    {
        static void Main(string[] args)
        {

            double[] x = { 0, 1, 2, 3, 4 };
            double[] y = { 1, 3, 5, 7, 9 };

            double Interpolate(double[] x, double[] y, double xi)
            {
                int i = 0;
                while (i < x.Length && xi > x[i])
                {
                    i++;
                }

                if (i == 0 || i == x.Length)
                {
                    throw new Exception("xi is out of range");
                }

                double x0 = x[i - 1];
                double x1 = x[i];
                double y0 = y[i - 1];
                double y1 = y[i];

                double yi = y0 + ((xi - x0) / (x1 - x0)) * (y1 - y0);

                return yi;
            }

            Console.WriteLine(Interpolate(x, y, 2.5)); // 6

        }

    }
}