[백준] 백준 9663 N-Queen (java)

N-Queen 문제는 백준에서 풀어보실 수 있습니다.
https://www.acmicpc.net/problem/9663

저는 개발자 지망생으로 공부하고 있는 대학생입니다.
때문에 아직 많이 부족합니다.

아래의 코드가 해당 문제를 풀 수 있는 코드는 맞지만, 해당 문제를 풀기위한 가장 좋은 코드는 아닙니다.
코드에 문제가 있거나, 부족한 점이 있다면 댓글 달아주시면 감사히 배우겠습니다.
감사합니다.

N-Queen 문제

해당 문제는 N*N 의 체스판위에 N개의 Queen을 배치하는데 서로 한번에 공격할 수 없는 위치에 배치할 수 있는 경우의 수를 구하는 문제입니다.

입력과 출력은 아주 간단하지만, 해결하는데에는 조금 고민이 필요한 문제라고 생각합니다.

전체 코드

우선 제 전체 코드입니다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

/**
* 퀸 N개가 N*N의 보드에 모두 위치하기 위해서는
* 각 행, 열 마다 하나씩의 퀸이 배치되어야 한다.
*/

public class Main {
    private static int answer;
    private static int boardLength;
    private static int[] board;

    public static void main(String[] args) throws IOException {
        init();
        calcNQueen(0);
        System.out.println(answer);
    }

    // 객체 값 초기화
    private static void init() throws IOException {
        answer = 0;
        boardLength = readConsole();
        board = new int[boardLength];
    }

    // 콘솔에서 데이터 읽어오기
    private static int readConsole() throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        return Integer.parseInt(br.readLine());
    }

    // 가능한 Queen의 개수 계산
    private static void calcNQueen(int count) {
        if (count == boardLength) {
            answer++;
            return;
        }

        for(int i = 0; i < boardLength; i++) {
            if(isQueenPossible(count, i)) {
                board[count] = i;
                calcNQueen(count+1);
            }
        }
        return;
    }

    // 해당 위치에 Queen이 위치할 수 있는지 판단.
    private static Boolean isQueenPossible(int count, int data){

        // 기존 Queen과 같은 row인 경우 false
        for(int i = 0; i < count; i++) {
            if(board[i] == data) {
                return false;
            }
        }

        // 기존 Queen에 대각선에 위치한 경우 false
        for(int i = 0; i < count; i++) {
            if(board[i] + (count - i) == data || board[i] - (count - i) == data ) {
               return false;
            }
        }
        return true;
    }
}

풀이 방법

이 문제를 풀이할 때 가징 중요한 것은 Queen의 특성을 이용하여 규칙을 생각해내는 것입니다.

Queen은 총 8가지 방향으로 무한대로 뻗어나갈 수 있기 때문에
그 규칙은 각 row, column 별로 하나의 Queen만이 위치할 수 있다는 것입니다.

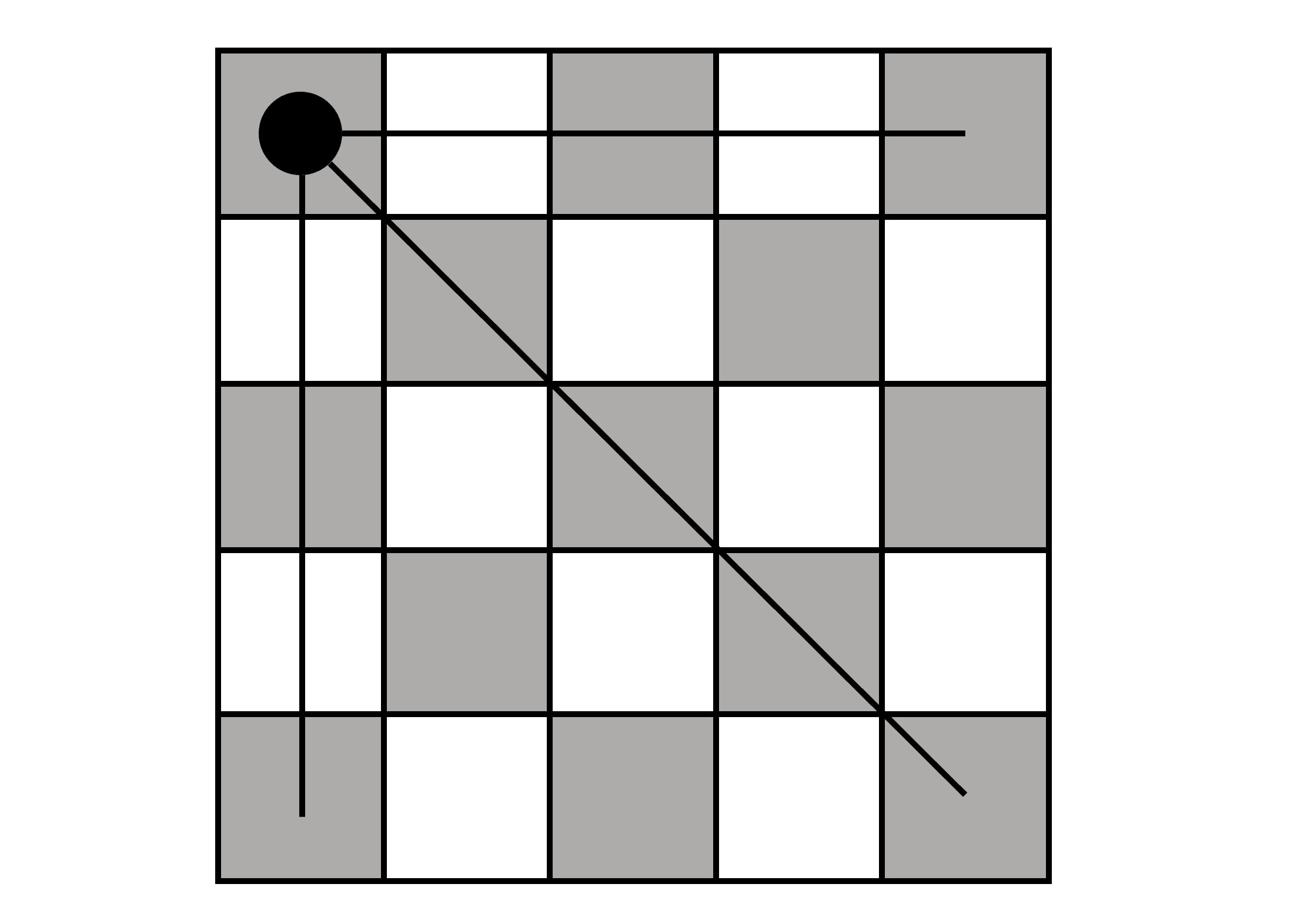
일단 대각선은 논외로 치더라도 위의 그림처럼 Queen이 특정 위치에 배치되면, 해당 좌표의 row와 column에는 Queen이 배치될 수 없습니다.

사실 이 가정을 하기까지 오래걸렸지, 이 생각을 하고나면, 문제가 쉽게 느껴졌던 것 같습니다.

이 규칙을 생각한 후, 제가 풀이한 방법은 재귀 함수와 객체의 변수를 활용한 것입니다.

객체의 필드를 활용하면, 재귀를 몇번 반복하고, 어떻게 반복하더라도 일정한 값을 유지할 수 있기 때문에 이를 활용하여 모든 Queen이 한번에 공격되지 않는 위치에 배치가 된 경우 해당 변수의 값을 증가시키는 방법으로 경우의 수를 셀 수 있었습니다.

필드 설명

answer : 정답을 체크하기 위한 변수 입니다.(계속 1씩 증가합니다)
boardLength : 문제에서의 N 값입니다.
board : 체스판입니다. (index는 column, value는 row라고 생각하시면 됩니다.)

private static int answer;
private static int boardLength;
private static int[] board;

1. 가능한 Queen을 찾는 메소드입니다.

count는 board의 index값으로 column이라고 생각하시면 됩니다.

즉 index값이 boardLength인 경우는 모든 Queen이 알맞은 위치에 배치되어 있는 상황을 의미하고, 이 경우 새로운 경우의 수를 찾은 것이기 때문에 answer를 1증가시키고 return합니다.

그렇지 않다면, 재귀를 활용하여 다른 가능한 경우의 수를 탐색하는 형태입니다.

// 가능한 Queen의 개수 계산
private static void calcNQueen(int count) {
    if (count == boardLength) {
        answer++;
        return;
    }

    for(int i = 0; i < boardLength; i++) {
        if(isQueenPossible(count, i)) {
            board[count] = i;
            calcNQueen(count+1);
        }
    }
    return;
}

2. Queen이 해당 위치에 배치되어도 괜찮은지 판단하는 메소드 입니다.

이전에 배치된 Queen들과 배치를 비교하여, 같은 row에 있거나(column은 count 값이기 때문에 겹칠 수 없습니다.) 대각선 상에 위치하는 경우 false를, 그렇지 않은 경우 true를 return하는 형태입니다.

// 해당 위치에 Queen이 위치할 수 있는지 판단.
private static Boolean isQueenPossible(int count, int data){

    // 기존 Queen과 같은 row인 경우 false
    for(int i = 0; i < count; i++) {
        if(board[i] == data) {
            return false;
        }
    }

    // 기존 Queen에 대각선에 위치한 경우 false
    for(int i = 0; i < count; i++) {
        if(board[i] + (count - i) == data || board[i] - (count - i) == data ) {
           return false;
        }
    }
    return true;
}