[백준] 2458번 키 순서

🔔 문제

1번부터 N번까지 번호가 붙여져 있는 학생들에 대하여 두 학생끼리 키를 비교한 결과의 일부가 주어져 있다. 단, N명의 학생들의 키는 모두 다르다고 가정한다. 예를 들어, 6명의 학생들에 대하여 6번만 키를 비교하였고, 그 결과가 다음과 같다고 하자.

• 1번 학생의 키 < 5번 학생의 키
• 3번 학생의 키 < 4번 학생의 키
• 5번 학생의 키 < 4번 학생의 키
• 4번 학생의 키 < 2번 학생의 키
• 4번 학생의 키 < 6번 학생의 키
• 5번 학생의 키 < 2번 학생의 키

이 비교 결과로부터 모든 학생 중에서 키가 가장 작은 학생부터 자신이 몇 번째인지 알 수 있는 학생들도 있고 그렇지 못한 학생들도 있다는 사실을 아래처럼 그림을 그려 쉽게 확인할 수 있다. a번 학생의 키가 b번 학생의 키보다 작다면, a에서 b로 화살표를 그려서 표현하였다.
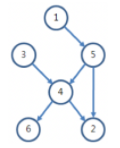1번은 5번보다 키가 작고, 5번은 4번보다 작기 때문에, 1번은 4번보다 작게 된다. 그러면 1번, 3번, 5번은 모두 4번보다 작게 된다. 또한 4번은 2번과 6번보다 작기 때문에, 4번 학생은 자기보다 작은 학생이 3명이 있고, 자기보다 큰 학생이 2명이 있게 되어 자신의 키가 몇 번째인지 정확히 알 수 있다. 그러나 4번을 제외한 학생들은 자신의 키가 몇 번째인지 알 수 없다.

학생들의 키를 비교한 결과가 주어질 때, 자신의 키가 몇 번째인지 알 수 있는 학생들이 모두 몇 명인지 계산하여 출력하는 프로그램을 작성하시오.

입력
첫째 줄에 학생들의 수 N (2 ≤ N ≤ 500)과 두 학생 키를 비교한 횟수 M (0 ≤ M ≤ N(N-1)/2)이 주어진다. 다음 M개의 각 줄에는 두 학생의 키를 비교한 결과를 나타내는 두 양의 정수 a와 b가 주어진다. 이는 번호가 a인 학생이 번호가 b인 학생보다 키가 작은 것을 의미한다.

출력
자신이 키가 몇 번째인지 알 수 있는 학생이 모두 몇 명인지를 출력한다.

🎯 풀이방법

플로이드-워셜 알고리즘

플로이드-워셜 알고리즘(Floyd-Warshall Algorithm)은 그래프에서 가능한 모든 노드 쌍에 대해 최단 거리를 구하는 알고리즘이다. 다익스트라 알고리즘과는 달리 모든 노드 쌍에 대해 최단 거리를 구하고, 음의 가중치를 가지는 그래프에서도 쓸 수 있다는 것이 특징이다.

요약하자면, N^3의 3중 for문을 돌면서 현재 갖고 있는 (출발지-도착지)의 최단경로 값이 빠른지, (출발지-경유지)+(경유지-도착지)의 최단경로 값이 빠른지 비교하는 알고리즘이다.
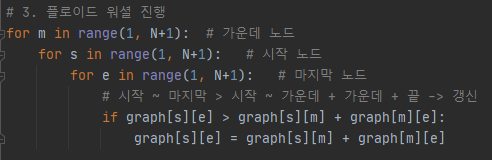N^3으로 모든 경우의 수를 체크하면서 최단 경로를 갱신한다. 단, 주의할 점은 for문에서 가운데 노드(=m, 경유지)가 제일 위에 있어야 한다. 결과적으로, graph[출발지][목적지]의 값은 최솟값임을 보장한다.

자신의 키가 몇 번째인지 알 수 있다는 모든 학생과의 비교가 가능하다와 동일하다. 즉, 거리가 무한대(∞)가 아닌 학생의 수가 N-1인 경우이다.

⏱ 시간복잡도

O(N) = N^3

💡 이 문제를 통해 얻어갈 것

플로이드-워셜 알고리즘 문제

이전에 풀어보면 좋은 문제 포스팅 : 백준 11404번 플로이드

💻 Python 코드

# 백준 2458번
MAX = 999999999

# N : 학생들의 수(=노드 갯수), M : 비교 횟수(=간선 갯수)
N, M = map(int, input().split())

# 1. 그래프 초기화
graph = [[MAX for j in range(N+1)] for i in range(N+1)]

# 2. 입력
for i in range(M):
    a, b = map(int, input().split())   # a < b
    graph[a][b] = 1

# 3. 플로이드 워셜 진행
for m in range(1, N+1):  # 가운데 노드
    for s in range(1, N+1):   # 시작 노드
        for e in range(1, N+1):   # 마지막 노드
            # 시작 ~ 마지막 > 시작 ~ 가운데 + 가운데 + 끝 -> 갱신
            if graph[s][e] > graph[s][m] + graph[m][e]:
                graph[s][e] = graph[s][m] + graph[m][e]


# 4. 모든 학생과의 비교가 가능한 경우
#      == 거리가 INF가 아닌 학생의 수가 N-1인 경우
answer = 0
for i in range(1, N+1):
    cnt = 0
    for j in range(1, N+1):
        if graph[i][j] != MAX or graph[j][i] != MAX:
            cnt += 1

    if cnt == N-1:
        answer += 1

print(answer)