"Semi-supervised learning에 대해 공부하였음. DSBA 수업 내용 정리"
-> 본 글은 강의 영상 내용을 정리한 것으로, 모든 내용이 영상에서 다루는 컨텐츠입니다. 혹시 문제되면 삭제하겠습니다.

Overview

Semi-supervised learning은 supervised learning task의 성능을 올리기 위해, unlabeled data를 어떻게 사용할 수 있는가에 대해 다룸. 새로운 모델이라기보다는 새로운 테크닉이라고 보는 게 더 적합함.

아래 사진에서 볼 수 있다시피, 왼쪽에 있는 데이터들은 (빨간색, 파란색 동그라미로 라벨링) labeled되어 있지만, 오른쪽에 있는 데이터들은 unlabeled data이다.

• 목적 : labeled data 하나만 사용하기보다는, 성능이 더 좋은 학습기를 만들기 위해 labeled data와 unlabeled data를 모두 사용하기 위함.
• 아래 그래프 해석 :
  (a) Labeled Data만 표시
  (b) Labeled and Unlabeled Data 표시. c학습기의 Decision boundary를 빨간색선으로 그려놓음 => 제대로 분류가 안되어있는 걸 확인할 수 있음.
  (c) Labeled Data를 이용한 Supervised Learning
  (d) Semi-Supervised Learning의 Decision boundary를 파란색으로 그려 놓음
  => (b)에서 보다 분류가 잘 되어있는 걸 확인할 수 있음.

용어정리

• Labeled data : LD
• Unlabeled data : UD

실제 예시 : Virtual Metrology based on FDC Data

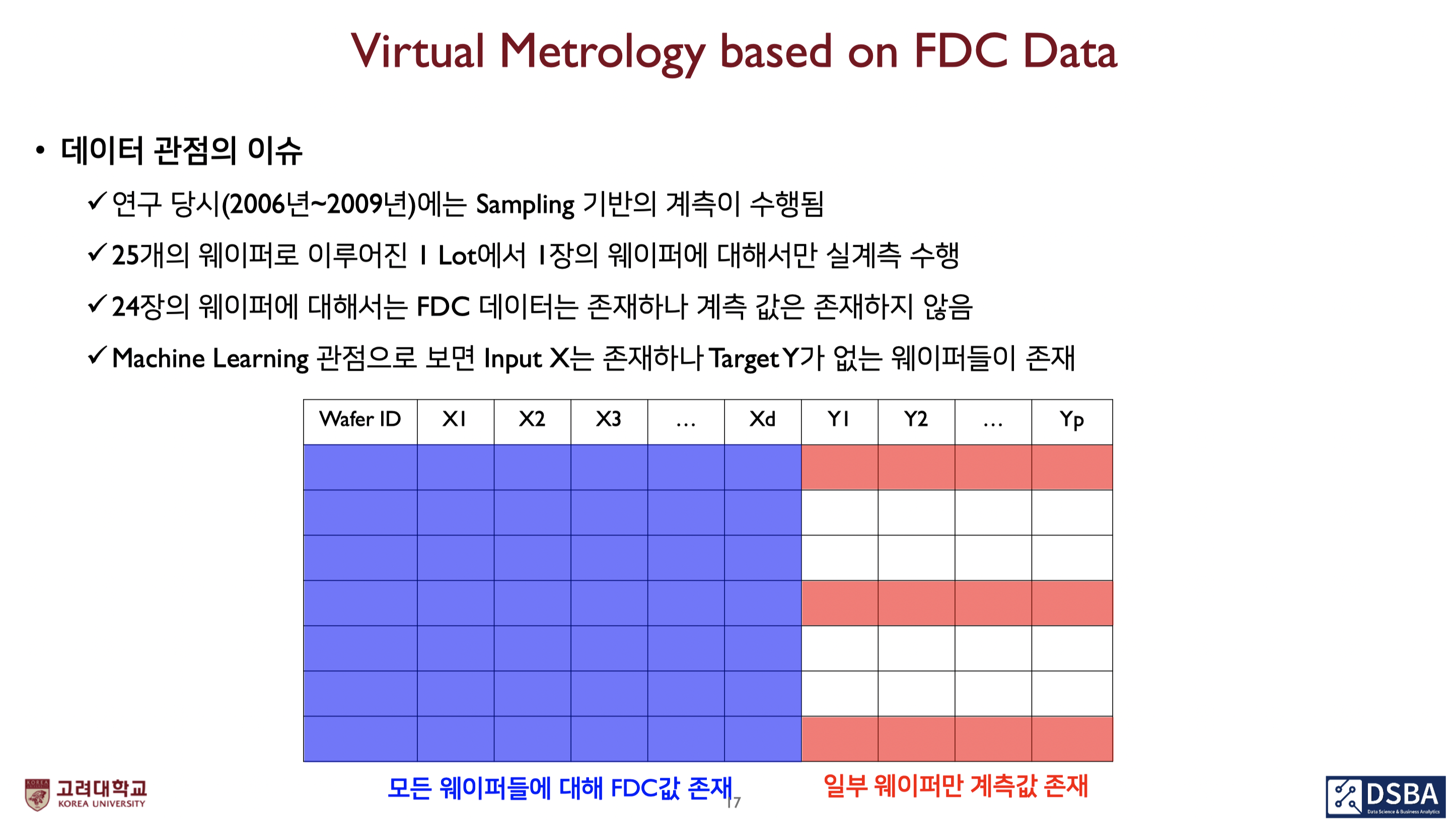
파란색이 칠해진 부분에는 y값, 즉 label이 없는 UD임
이렇게 UD도 사용하기 위해 SSL 방법론을 도입함
-> 방법론의 효과 : 실계측 정보(=LD)만 사용한 경우보다 예측 오차가 낮은 모형 구축 가능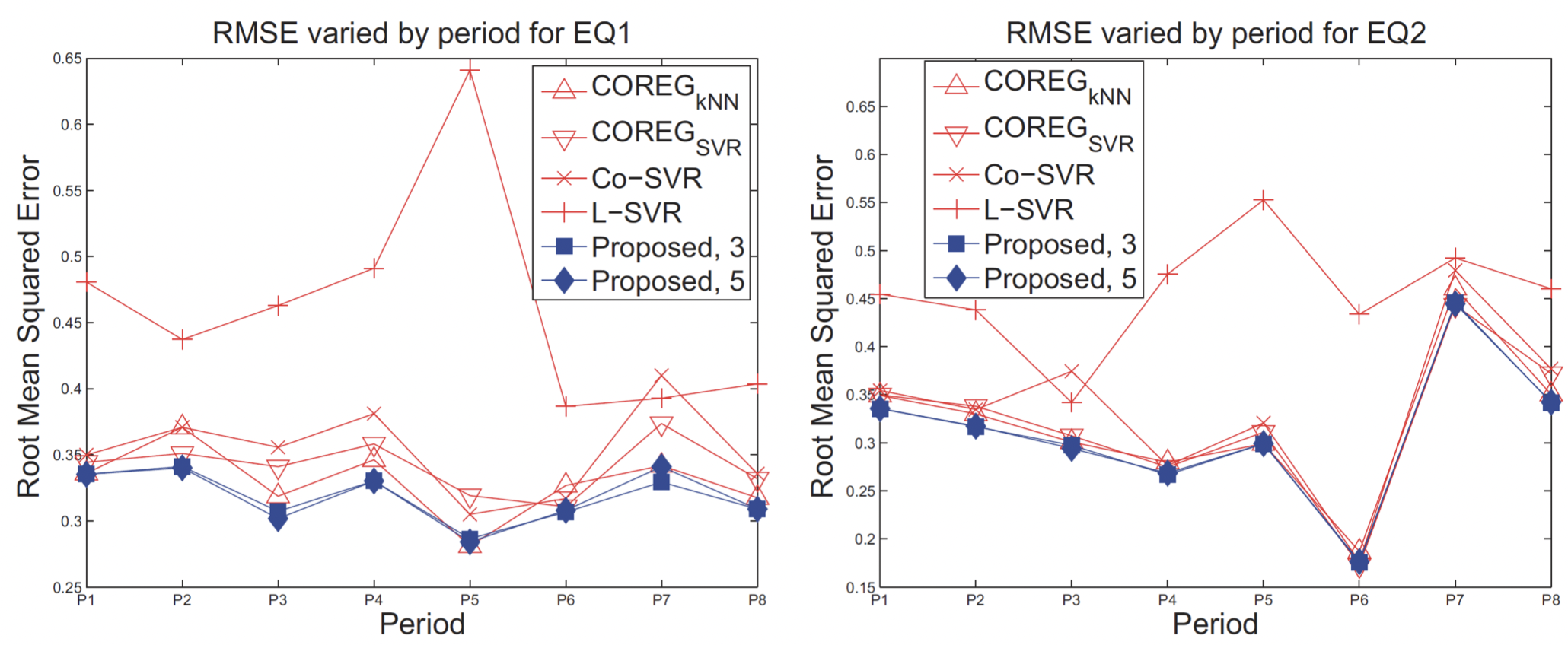

어떤 경우에 unlabeled data를 유용하게 사용할 수 있을까?

1. Uniformly distributed data do not help : 즉, 데이터가 완벽하게 uniform하면 안되고, 어느정도 클러스터로 분류가 가능한 분포를 띄고 있어야함.
2. Must use properties of $\operatorname{Pr}(\mathbf{x})$
   

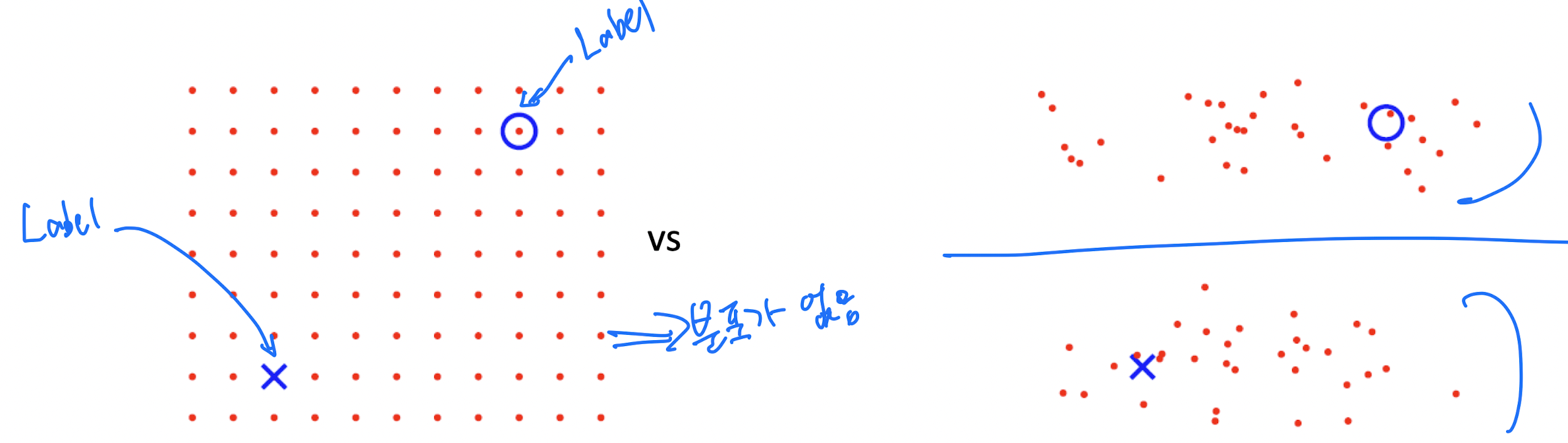
• 왼쪽 그림 : LD는 파란색 O, X로 표시되어 있고, 나머지 빨간색 점들은 모두 UD이다. 그런데 UD에 특정한 분포가 없으므로 이 경우엔 분류가 힘들다.
• 오른쪽 그림 : 반면 여기에선, 데이터가 어느정도 분포를 띄고 있기 때문에 파란색 선처럼 class를 분류하는 Decision boundary를 찾을 수 있다.

The effect of SSL

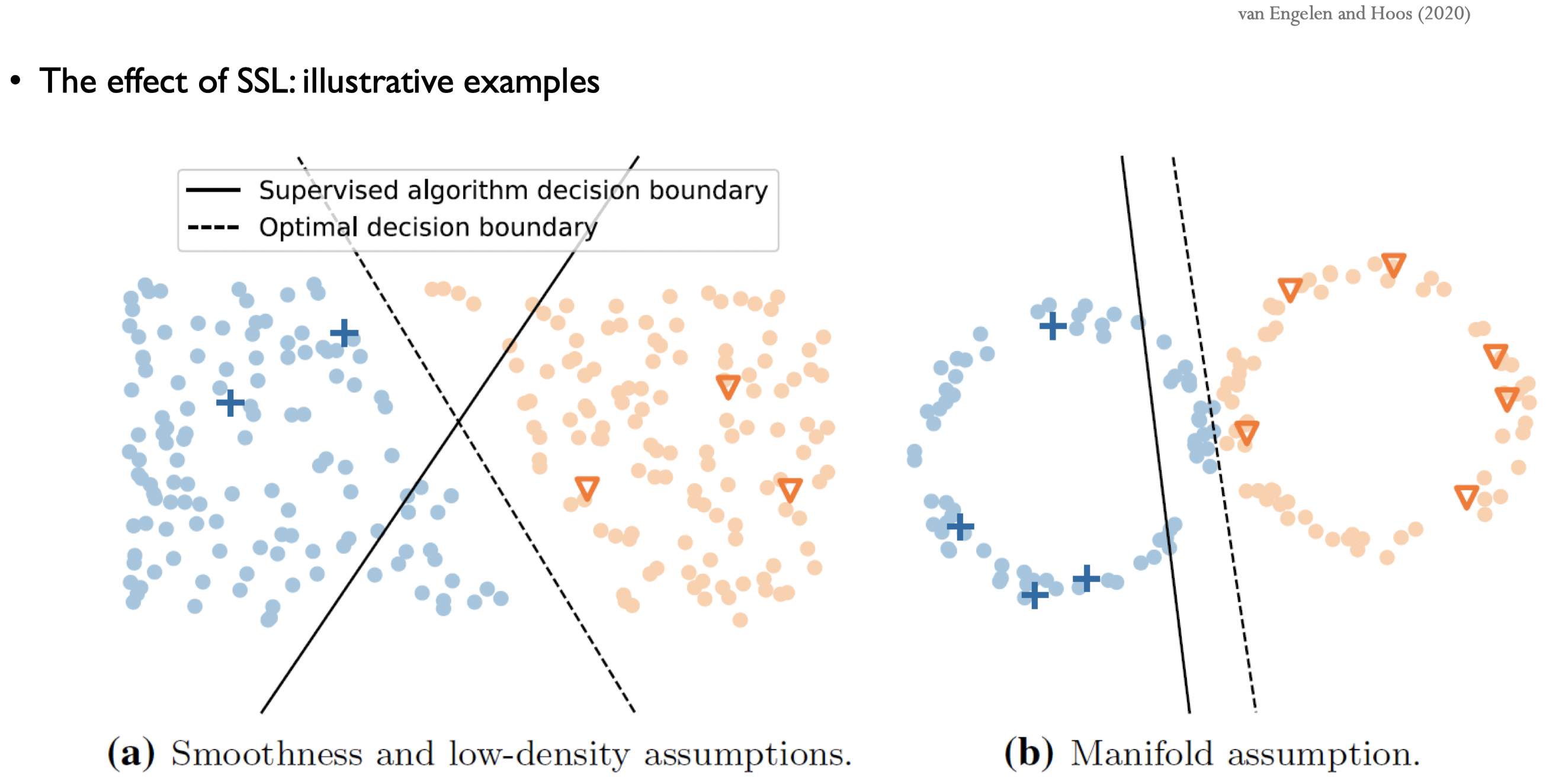
마크되어 있는 것들은 LD이고, 나머지는 모두 UD이다.

(a) Smoothness and low-density assumptions

• 여기에선 두가지를 가정한다.

1. 데이터들이 범주 내에서 smmoth하게 되어있고,
2. 범주 내에 존재하지 않는 데이터들은 density가 낮다.

• 결과

1. LD만 사용해서 학습한 classifier : 실선을 decision boundary로 채택할 테고, 잘 분류하지 못하는 모습으로 보인다.
2. UD도 함께 사용해서 학습한 classifier : 점선을 decision boundary로 채택할테고, LD만 사용한 것보다 더 분류를 잘하는 모습이 보인다.

(b) Manifold assumption

• 가정 : 데이터들이 manifold를 형성하고 있다.
• 결과 : (a)와 동일하게 UD를 함께 사용하여 학습한 것이 더 잘 분류를 한다.

Decision boundary shift

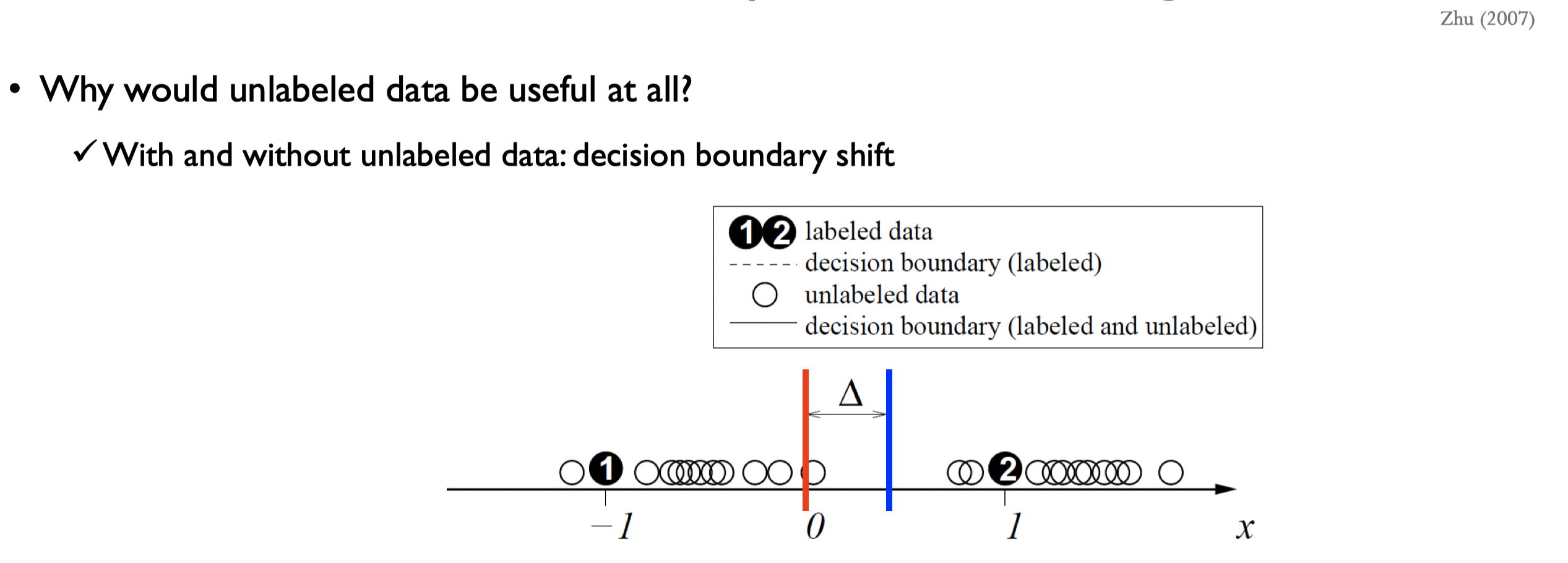
Decision boundary가 바뀌는 것을 좀 더 자세히 살펴보자.

• RED : LD만 사용하여 만든 decision boundary
• BLUE : UD도 함께 사용하여 만든 decision boundary
  UD를 사용하면 decision boundary가 빨간색선에서 파란색선으로 옮겨가는 걸 볼 수 있다.

그렇다면 UD는 항상 도움이 되는가? => 그렇지는 않다.

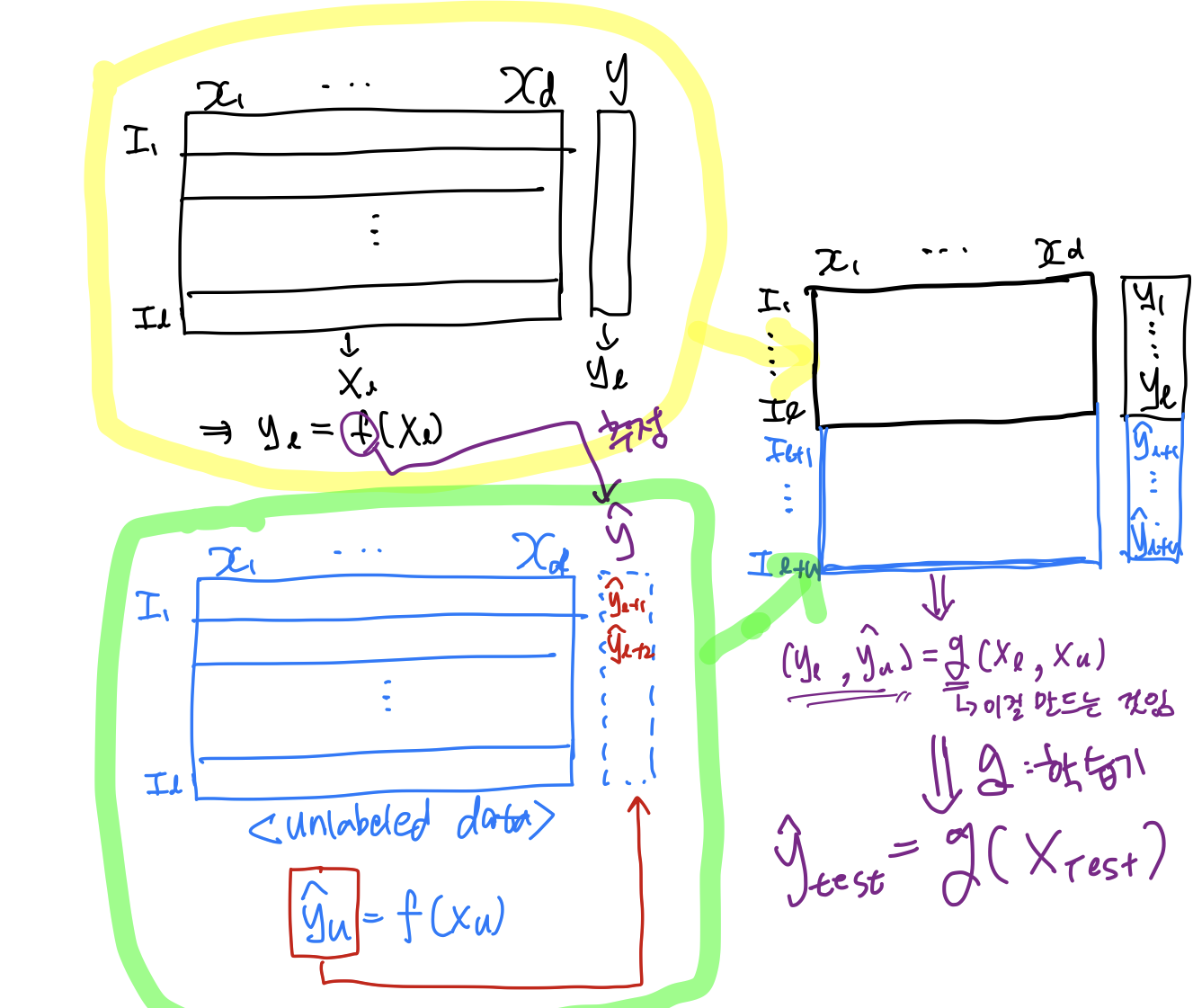
Notations

• Input instance $\mathbf{X}$ : Input data, 즉 설명변수에 해당하는 vector
• label $y$ : label
• Learner $f: \mathcal{X} \mapsto \mathcal{Y}$ (모델f)
• Labeled data $\left(\mathbf{X}_{l}, \mathbf{y}_{l}\right)=\left\{\left(\mathbf{x}_{1: l}, y_{1: l}\right)\right\}$
• Unlabeled data $\mathbf{X}_{u}=\left\{\left(\mathbf{x}_{l+1: n}\right)\right\}$
  : y가 존재하지 않고, X만 존재. 학습과정에서 사용가능
  => Transductive learning은 이러한 $\mathbf{X}_{u}$를 맞추는 과정임.
• Usually $l \ll n$
• Test data $\mathbf{X}_{\text {test }}=\left\{\left(\mathbf{x}_{n+1:}\right)\right\}$
  : 학습과정에서 사용하지 않고, test시에만 사용.

Semi-supervised learning vs. Transductive learning

흔히 두 개념을 혼용해서 쓰곤 하는데, 엄밀히 말하면 서로 다른 개념

• Semi-supervised learning : is ultimately applied to the test !
  data (inductive).
  -> $\mathbf{X}_{\text {test }}$를 맞추는 것
• Transductive learning : is only concerned with the unlabeled data.
  -> $\mathbf{X}_{u}$를 맞추는 것

Taxonomy

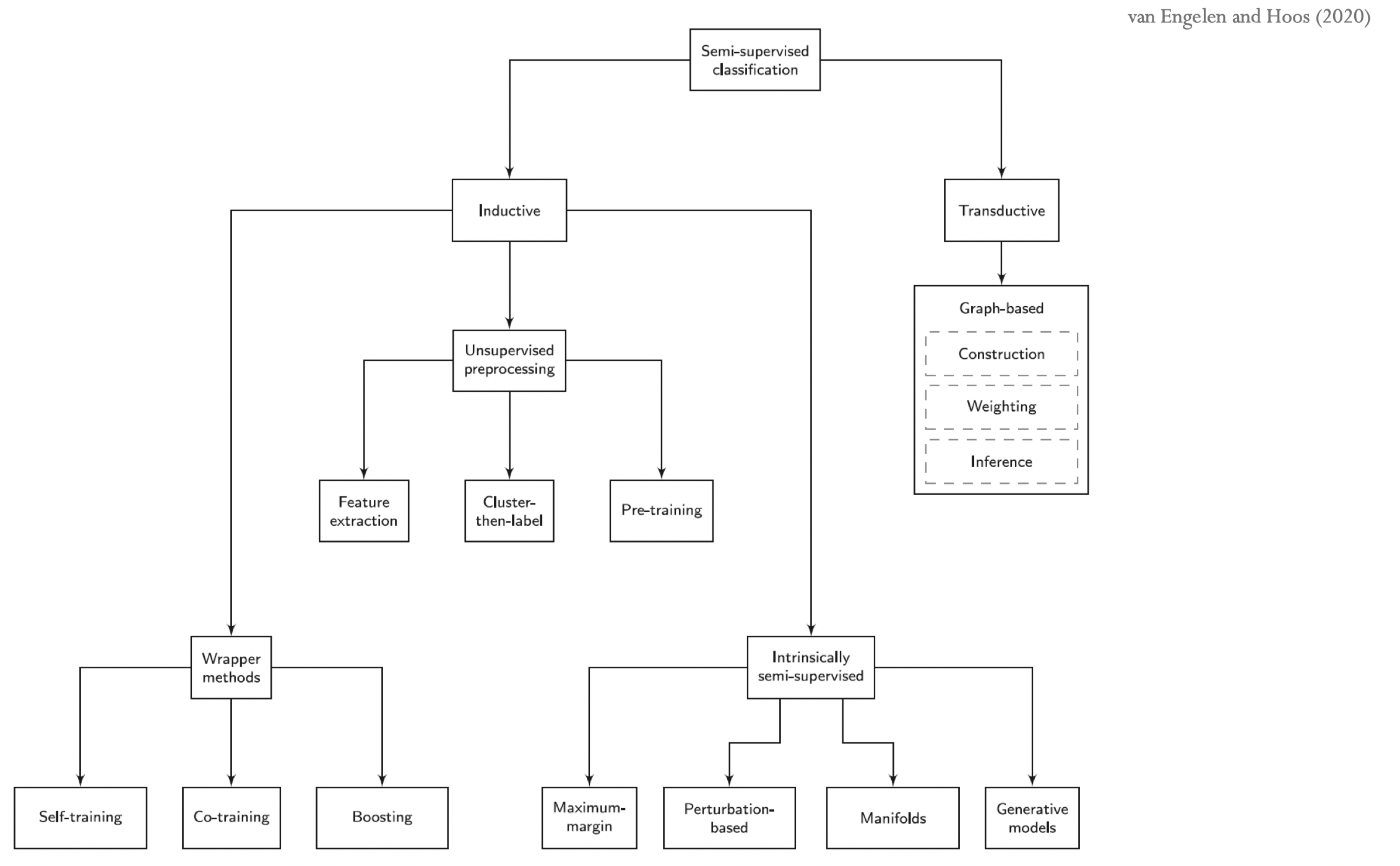
Self-Training and Co-Training

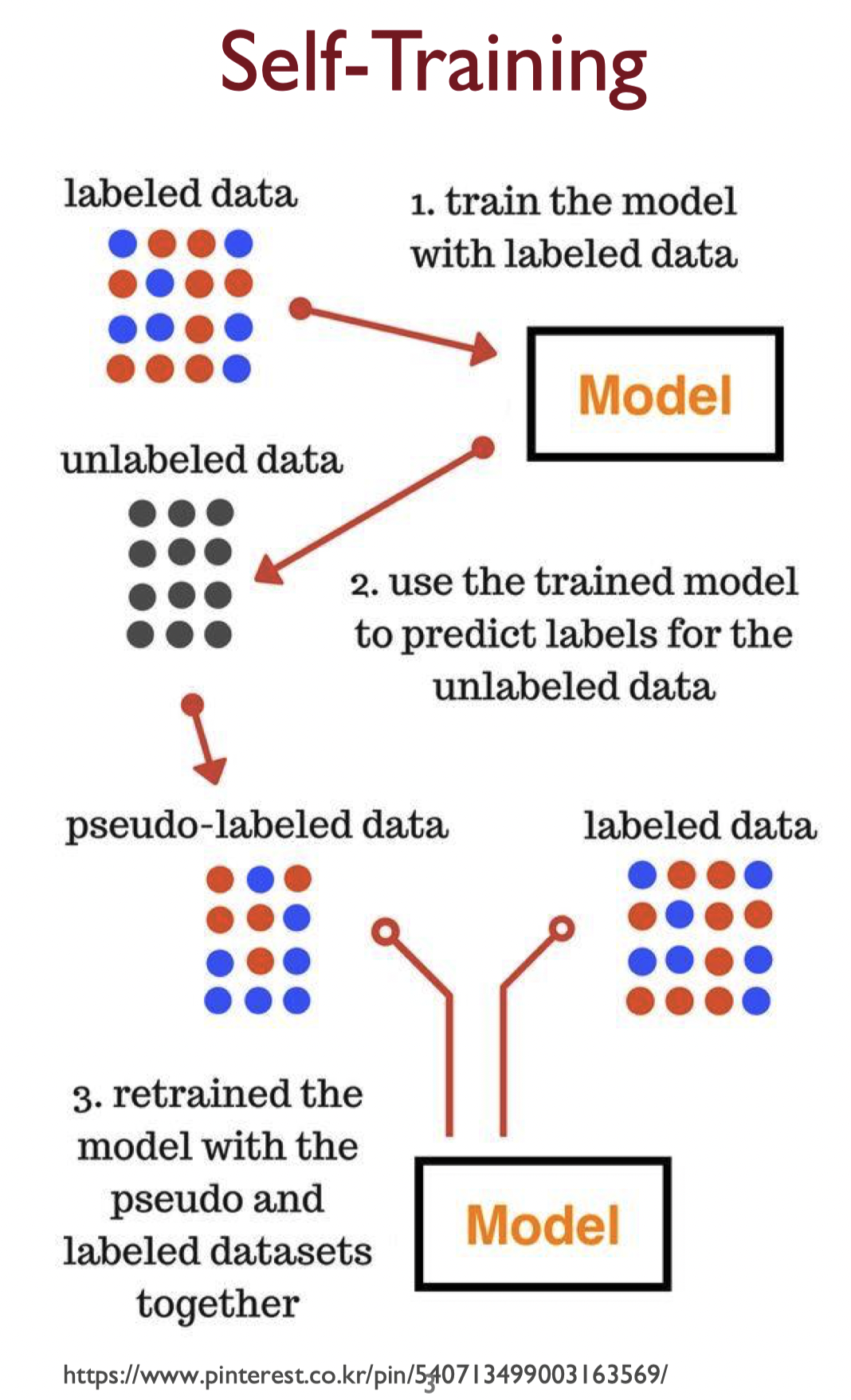
Self-Training

self-training의 가정

높은 confidence predictions는 정답일 확률이 높다. (One's own high confidence predictions are correct.)

Basic self-training algorithm

1. Train $f$ from $\left(\mathbf{X}_{l}, \mathbf{y}_{l}\right)$ : LD를 이용해서 학습 진행
2. Predict on $\mathbf{x} \in \mathbf{X}_{u}$ : UD를 예측
3. Add $(\mathbf{x}_u, f(\mathbf{x_u}))$ to labeled data : 2번에서 예측한 UD에서 선별된 데이터를 LD에 포함시킴
4. 위 과정 반복

• Variations in self-training
  - 소수의 confident한 $(\mathbf{x}_u, f(\mathbf{x_u}))$만 LD에 포함시키기
  - 모든 $(\mathbf{x}_u, f(\mathbf{x_u}))$를 LD에 포함시키기
  - confidence에 따라 가중치(weight)를 부여하여 $(\mathbf{x}_u, f(\mathbf{x_u}))$를 LD에 포함시키기

Example 1 : probability 값을 이용

1. Train a naive Bayes classifier on the two initial labeled images.
2. 1번 모델로 UD를 분류하고, $\log p(y=\text { astronomy } \mid x)$ confidence에 따라 정렬한다.
3. Log probability가 굉장히 작은 데이터는 사용하지 않고, Log probability가 0에 가까운(확률값이 1에 가까운) 데이터만 정답데이터로 간주하고 데이터셋에 포함시킨다.
4. 1-3번과정을 반복한다.

Example 2 : Propagating I-Nearest Neighbor

KNN에서 k=1인 걸로 propagation을 진행하는 방법.

• Input
  • LD : $\left\{\left(\mathbf{x}_{i}, y_{i}\right)\right\}_{i=1}^{l}$
  • UD : $\left\{\mathbf{x}_{j}\right\}_{j=l+1}^{l+u}$
• distance function : $d()$
• process
  1. Initially, let $L=\left\{\left(\mathbf{x}_{i}, y_{i}\right)\right\}_{i=1}^{l} \text { and } U=\left\{\mathbf{x}_{j}\right\}_{j=l+1}^{l+u}$
  2. UD의 집합 $U$이 empty가 될 때까지 반복 :
     3. Select $\mathbf{x}=\operatorname{argmin}_{\mathbf{x} \in U} \min _{\mathbf{x}^{\prime} \in L} d\left(\mathbf{x}, \mathbf{x}^{\prime}\right)$
        가장 가까운 객체 하나를 찾음
     4. Set $f(\mathbf{x})$ to the label of $\mathbf{x}$'s nearest instance in $L$.
        Break ties randomly.
        찾은 객체에 nearest label의 label을 붙여줌.
     5. Remove $\mathbf{x}$ from $U$; add $(\mathbf{x}, f(\mathbf{x}))$ to $L$.
        이렇게 만들어진 pseudo-labeled data(pseudo-label이 주어진 객체)는 $U$에서 제외한다.

과정

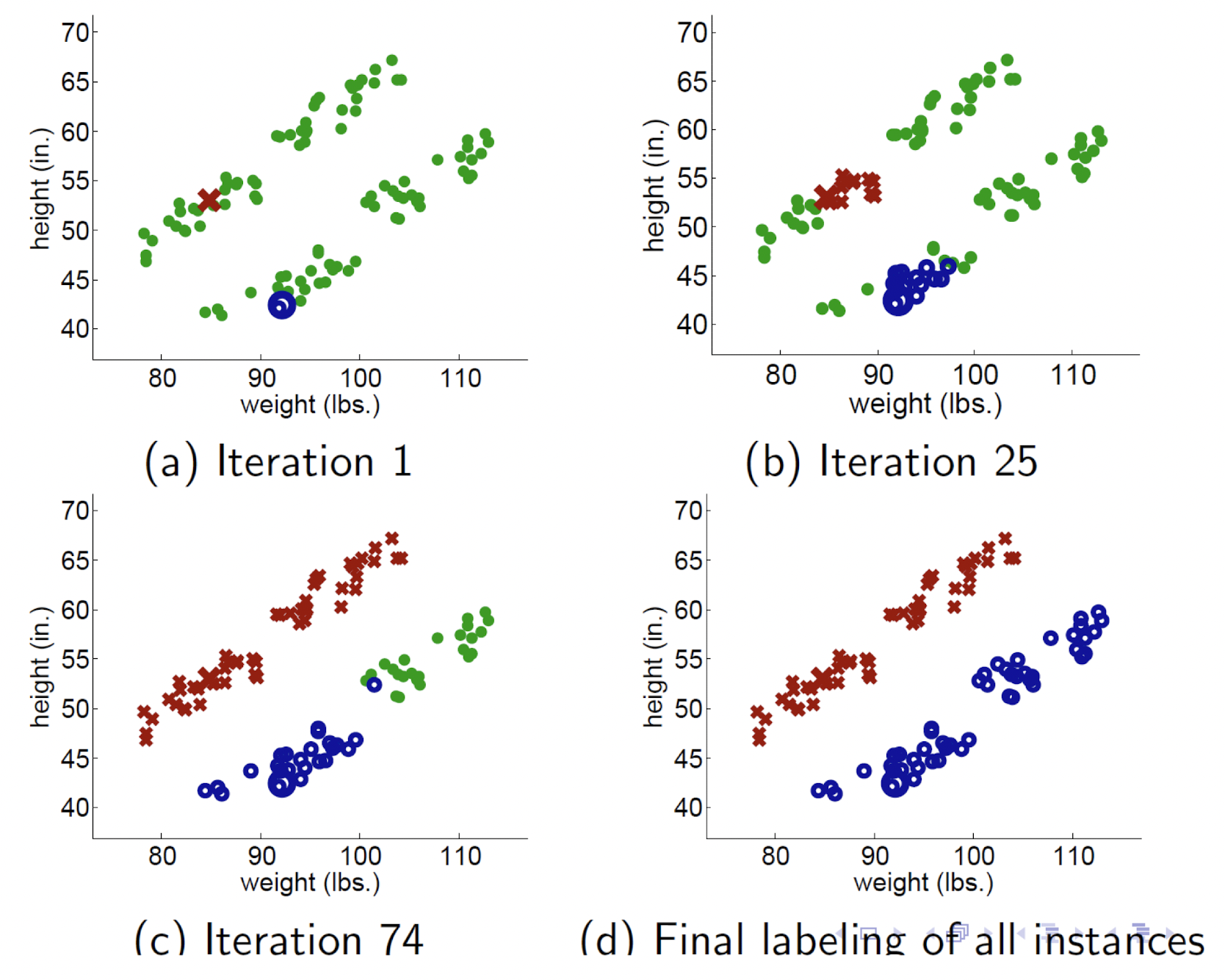
• 초록색 : UD
• 빨강색, 파랑색 : LD
• iteration이 늘어날수록 label이 점점 더 propagation 됨.

문제점 with a single outlier

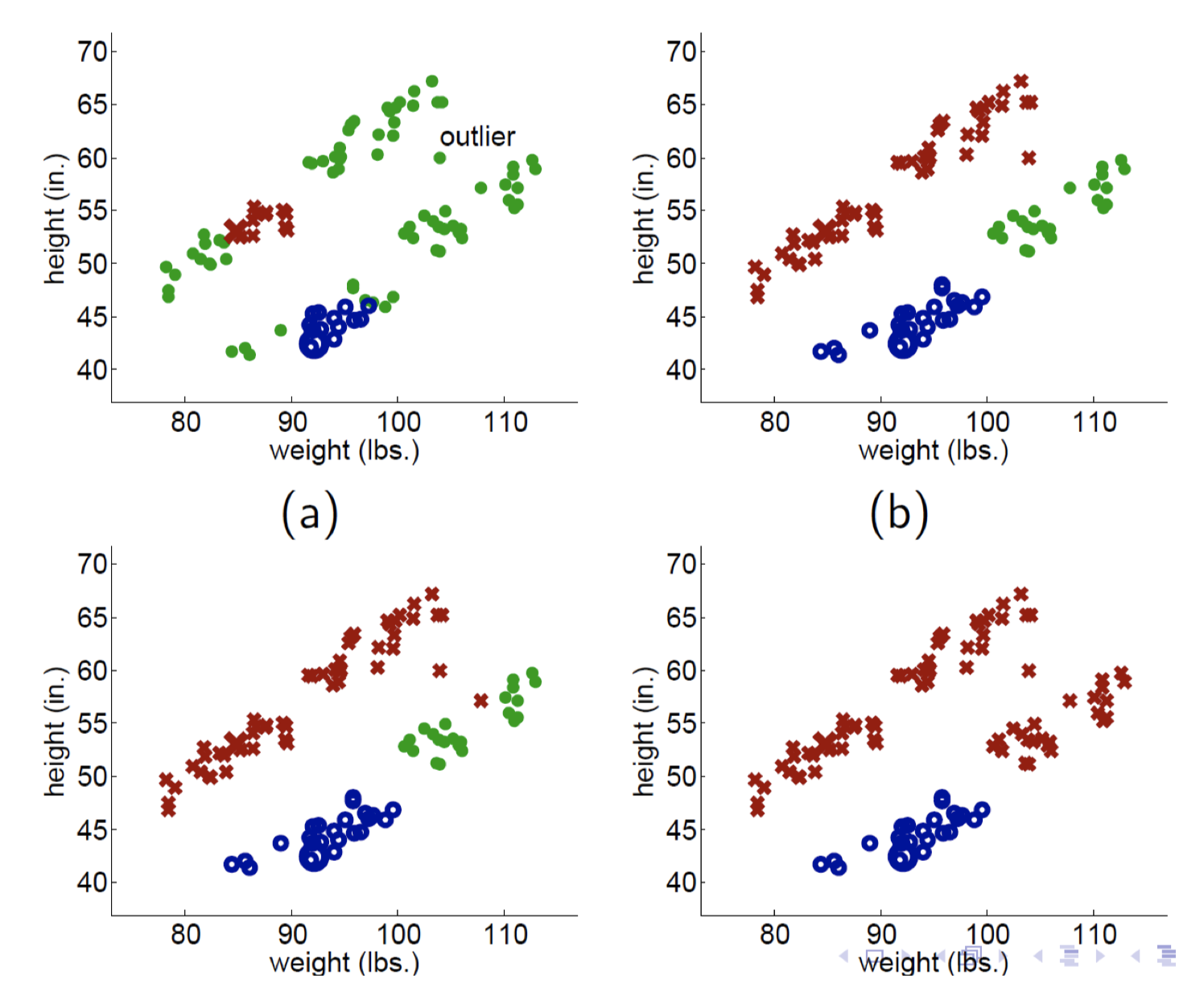
(a)에 존재하는 outlier 때문에, 빨간색 label이 더 많은 영역을 차지하게 되버림. 이러한 KNN propagation 방식은 outlier나 노이즈에 굉장히 민감함.

Self-Training : Summary

• 문제점
  • 초기에 한 번 분류가 잘못되면, 그거때문에 연쇄적으로 잘못 분류됨.
  • 항상 converge한다는 보장이 없음

=> 지금 소개한 방식들은 오래된 기본적인 구식의 방식임. 새로운 방식들을 소개하겠음.

Multi-view Algorithm: Co-Training

핵심 가정 : "어떤 특정한 객체를 포함하거나 설명하는 데 있어서 mutually exclusive(상호 배반적)인 feature sets이 존재할 것이다"

예시 : eclipse와 car의 분류

이클립스와 자동차는 '이미지'라는 feature로도 설명할 수 있지만, '텍스트'라는 feature로도 설명이 가능하다.

여기서 가장 중요한 가정! : 하나의 객체(클래스)를 표현하는 데 이미지와 텍스트라는 피쳐셋은 서로 굉장히 다를 것이다. 이 피쳐셋들은 서로 mutually exculsive할 것이다 라고 가정하는 것임.

중요한 특징, Feature split

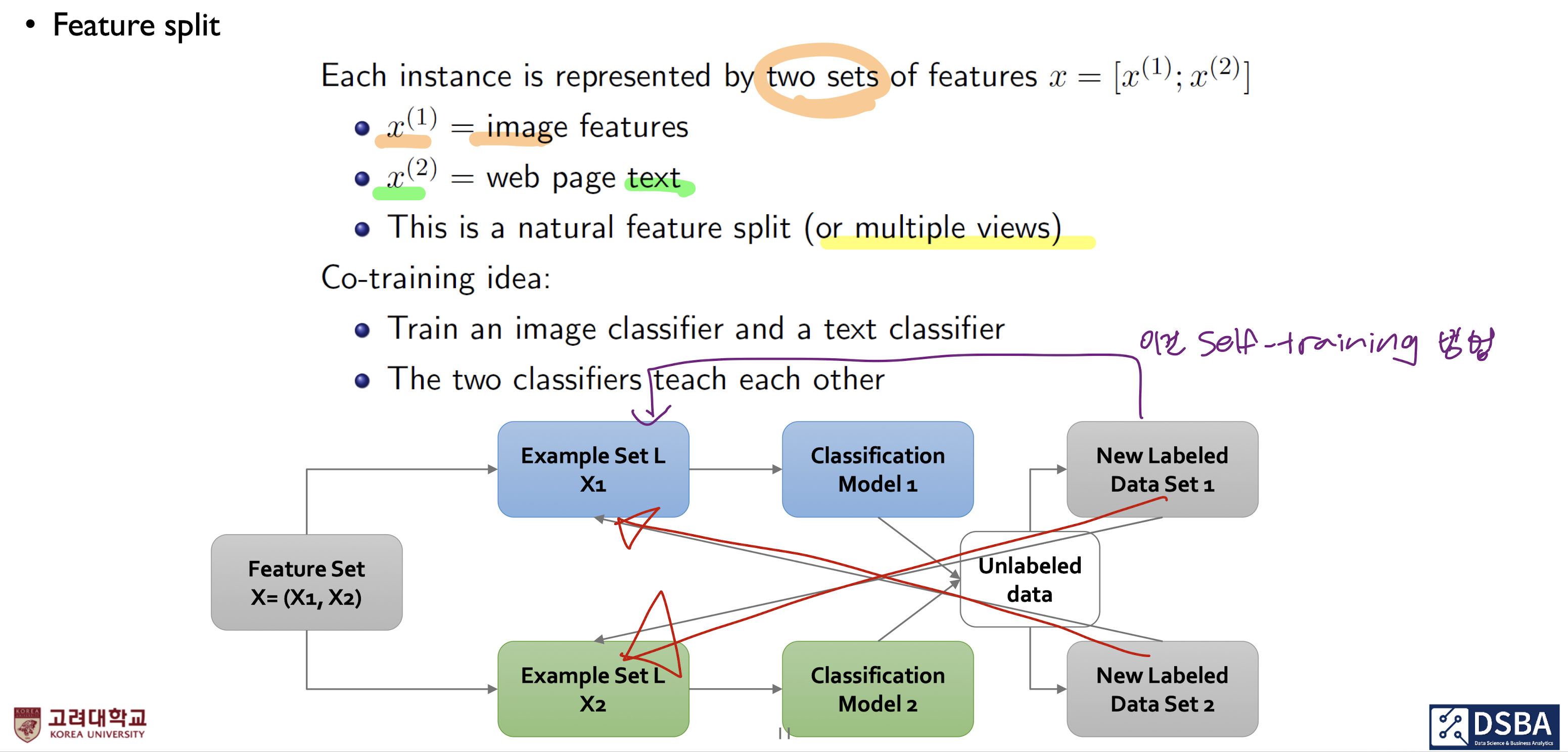
• Co-training의 기본적인 가정 : 개별적인 객체는 두셋의 피쳐로 이뤄진다.
  • two sets of features : $x=\left[x^{(1)} ; x^{(2)}\right]$
    • $x^{(1)}$ : 이미지로 이뤄진 피쳐
    • $x^{(2)}$ : 텍스트로 이뤄진 피쳐
    • 다양한 관점에서 바라본다고 해서, Multiple views라고도 한다.
• Co-training 과정:
  1. Classification Model1 : 이미지를 이용해서 분류하는 classifier를 만들고,
  2. Classification Model2 : 텍스트를 이용해서 분류하는 classifier를 만들고,
  3. 그런 후에 한 쪽에서 굉장히 자신있게 분류한 데이터를 다른 쪽 분류기를 학습하는 데 사용함. (high confidence data -> 다른 분류기 학습에 사용)
     => 협동학습 !!
  4. 그 후 pseudo-label을 부여함.
     => 즉, 서로서로 상대방에게 Pseudo-labeled data를 넘겨주는 방식

Example

좀 더 확장된 논문

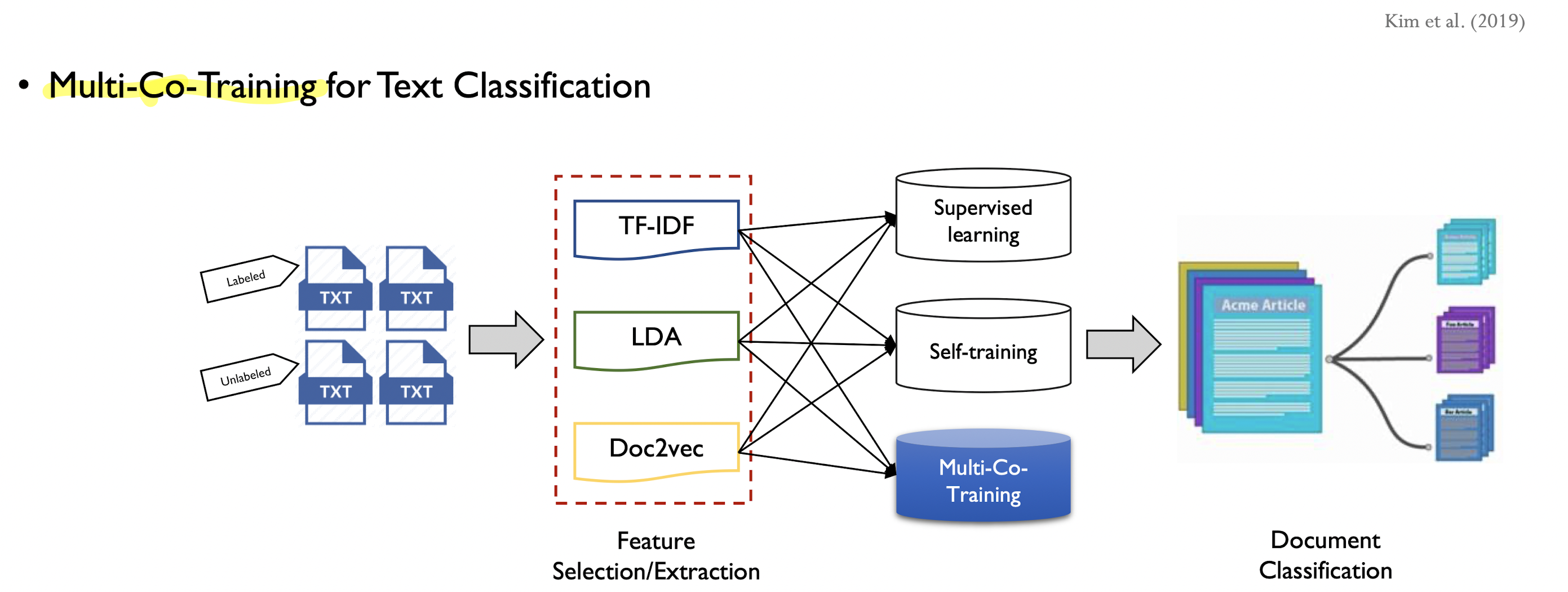
• 주제 : Document를 분류하는 것(문서분류)

• Feature sets: 문서 데이터를 가지고, 3가지의 형태로 feature 표현함.
  1. TF_IDF : 가장 고전적인 방식
  2. LDA: Topic modeling, 하나의 문서를 특정한 수로 정의된 토픽의 비중으로서
  현할 수 있음. 토픽을 뽑아내는 데도 사용할 수 있지만, 가변적인 길이를 갖는 문서에 대해 고정적인 길이의 벡터로 변환하는 Feature extracter로도 사용할 수 있음
  3. Doc2vec : neural network기반의 모델
  => 이 세가지를 이용해서 한 쪽에서 굉장히 높은 confidence를 갖는 unlabeled data를 나머지 두개의 데이터셋이 학습할 수 있도록 도와주는 것임.

• 추가 실험 : 이 세가지의 피쳐셋에 대해서 또 각각에 대한 실험을 수행하였음.
  1.SL만 했을 때 / 2.St만 했을 때 / 3.제안한 Mct했을 때 => 이 세가지 각각이 성능차이를 어떻게 내는가?

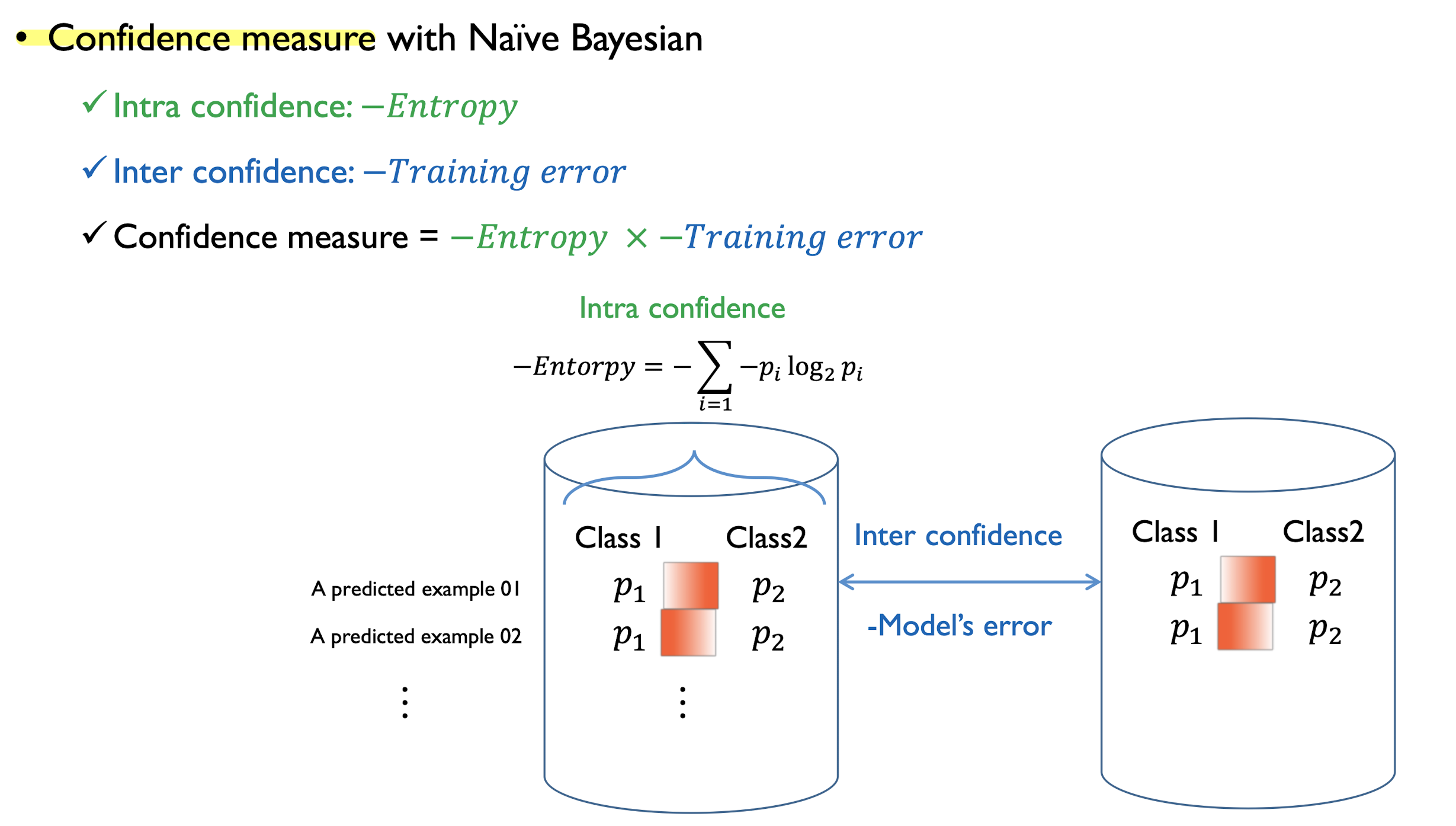
Confidence measure with Naive Bayesian

• 방식

  1. Intra confidence : 얼마나 현재 모델이 특정 두 범주에 대해 극단적인 예측을 하고 있는가 => Entropy로 계산
  2. Inter confidence : 현재 모델이 실질적으로 얼마나 잘 하고 있는가 => training error로 계산

• 결론 : 모델이 정확하고, 정확한 모델이 극단적인 범주에 대한 확률값의 차이를 나타낼 수록 해당하는 객체들은 pseudo-label이 정답일 가능성이 높으니 정답셋으로 인정해주자.

References

"Semi-supervised learning에 대해 공부하였음. DSBA 수업 내용 정리"
-> 본 글은 영상의 내용을 정리한 것으로, 모두 영상 내 컨텐츠임.
아래 References는 강의자료에서 언급하고 있는 References임