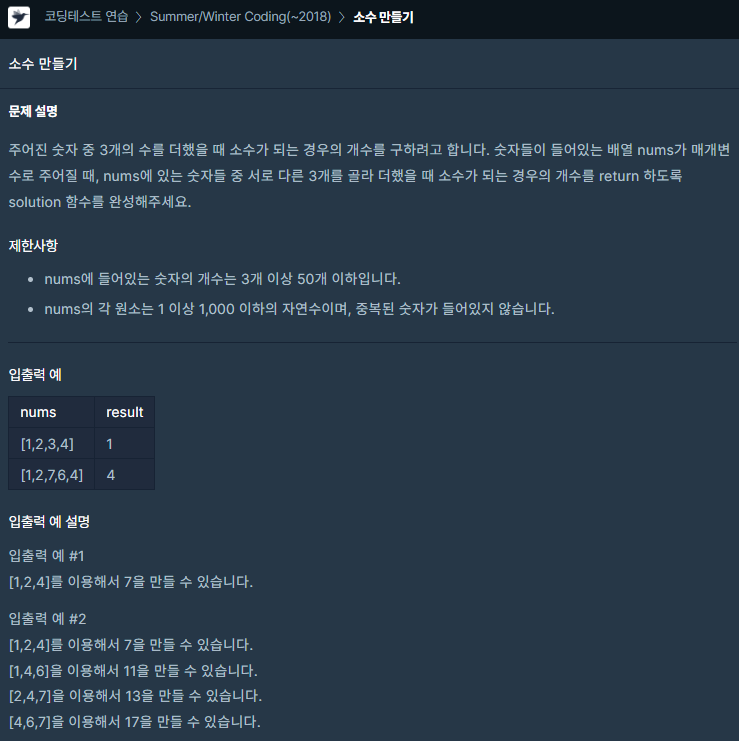
문제
정답 코드
class Solution {
public int solution(int[] nums) {
int answer = -1;
int tmp=0;
int count=0;
for(int i=0;i< nums.length;i++) {
for(int j=i+1;j< nums.length;j++) {
Loop1: for (int k=j+1;k< nums.length;k++) {
tmp = nums[i]+nums[j]+nums[k];
for(int l=2;l<tmp;l++) {
if(tmp%l==0) {
continue Loop1;
}
}
count++;
}
}
}
answer=count;
return answer;
}
}삼중 for문으로 tmp에 세 개의 수를 합친 값을 넣어 준 뒤, 어떻게 해야할까 고민했다.
소수라면 2 이상의 숫자로 나눴을 때 모든 수에서 나머지가 있을 것이기 때문에, 나머지가 0인 경우에는 count를 올리지 않도록 for문에 Loop1이라는 이름을 주고 continue로 다음 반복으로 보냈다.
다른 사람 풀이
int cnt = 0;
for(int i = 1; i <= (int)Math.sqrt(num); i ++){
if(num % i == 0) cnt += 1;
}
return cnt == 1;삼중for문 등 개념은 같았지만, 제곱근 이하의 숫자에서만 for문이 돌려서 소수를 탐색한다!?
소수 판별법: 제곱근
N의 약수는 무조건 sqrt(N)의 범위에 존재한다.
만약 N이 20이라고 한다면, 제곱근은 4.47 이다.
곱해서 20이 되는 값은
1*20, 2*10, 4*5, 5*4, 10*2, 20*1제곱근의 값을 기준으로 곱해지는 숫자가 반대로 바뀐다.
따라서 N의 제곱근까지 나누어 떨어지는지 여부를 조사하면 더 빠르게 소수판별을 할 수 있는 것이다!
이 덕분에 속도가 더 빨라지는 장점이 있다.

