Binary Search Tree 구현

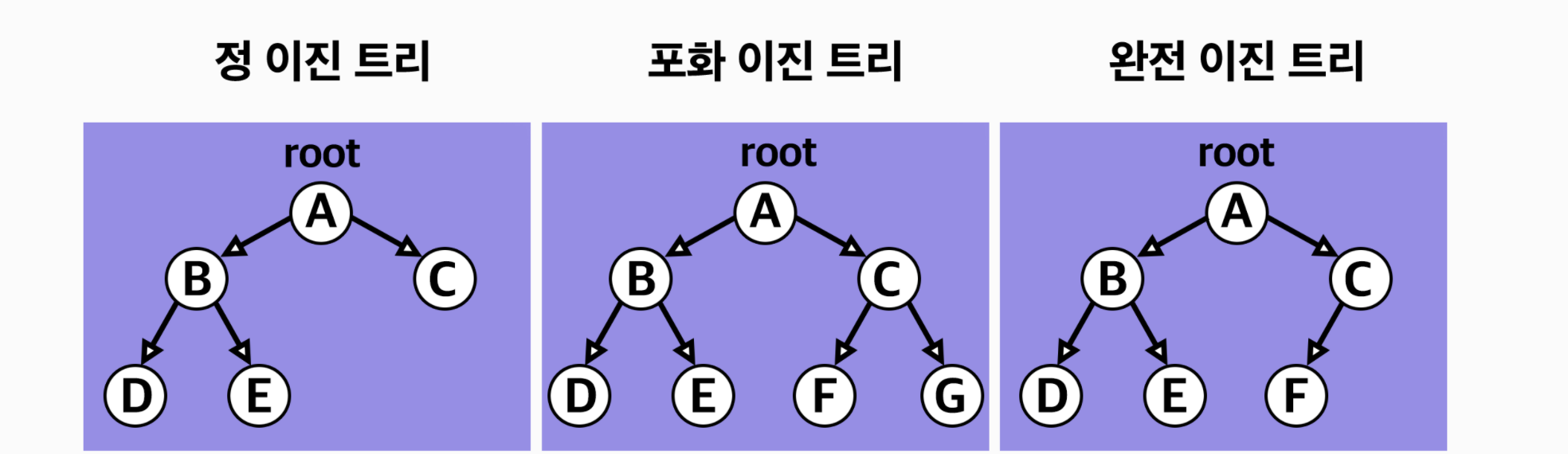
Implementation Binary Search Tree

문제: Tree 구현을 위한 기본적인 코드가 작성되어 있습니다. Binary Search Tree 자료구조의 특성을 이해하고 FILL_ME_IN 을 채워 테스트를 통과해주세요.

맴버 변수
입력 데이터를 담을 수 있는 value
노드를 왼쪽에 저장할 수 있는 Array 타입의 left
노드를 오른쪽에 저장할 수 있는 Array 타입의 right

메서드
insert(value): 입력받은 value를 Binary Search에 맞게 Tree에 계층적으로 추가할 수 있어야 합니다.
contains(value): 트리에 포함된 데이터를 찾을 수 있어야 합니다.
preorder(callback): 전위 순회를 통해 트리의 모든 요소에 callback을 적용할 수 있어야 합니다.
inorder(callback): 중위 순회를 통해 트리의 모든 요소에 callback을 적용할 수 있어야 합니다.
postorder(callback): 후위 순회를 통해 트리의 모든 요소에 callback을 적용할 수 있어야 합니다.

주의사항
value는 어떠한 값도 들어갈 수 있지만 현재 구현하는 Tree는 숫자로 제한합니다.

사용 예시

const rootNode = new BinarySearchTree(10);
rootNode.insert(7);
rootNode.insert(8);
rootNode.insert(12);
rootNode.insert(11);
rootNode.left.right.value; // 8
rootNode.right.left.value; //11

let arr = [];
rootNode.preorder((value) => arr.push(value * 2));
arr; // [20, 14, 16, 24, 22]
...

• 사용코드

class BinarySearchTree {
  constructor(value) {
		// constructor로 만든 객체는 이진 탐색 트리의 Node가 됩니다.
    this.value = value;
    this.left = null;
    this.right = null;
  }

	// 이진 탐색 트리의 삽입하는 메서드를 만듭니다.
  insert(value) {
		// 입력값을 기준으로, 현재 노드의 값보다 크거나 작은 것에 대한 조건문이 있어야 합니다.
		// 보다 작다면, Node의 왼쪽이 비어 있는지 확인 후 값을 넣습니다.
    if (value < this.value) {
      if (this.left === null) {
        this.left = new BinarySearchTree(value);
      } else {
        this.left.insert(value)
				// TODO: 비어 있지 않다면 해당 노드로 이동하여 처음부터 다시 크거나 작은 것에 대한 조건을 물어보아야 할 것입니다.
				// TIP: 재귀함수를 사용합니다.
      }
		// 보다 크다면, Node의 오른쪽이 비어 있는지 확인 후 값을 넣습니다.
    } else if (value > this.value) {
      if (this.right === null) {
        this.right = new BinarySearchTree(value);
      } else {
        this.right.insert(value);
				// TODO: 비어 있지 않다면 해당 노드로 이동하여 처음부터 다시 크거나 작은 것에 대한 조건을 물어보아야 할 것입니다.
				// TIP: 재귀함수를 사용합니다.
      }
		//그것도 아니라면, 입력값이 트리에 들어 있는 경우입니다.
    } else {
      // 아무것도 하지 않습니다.
    }
  }
  // 앞서 구현했던 트리에 비해 이진 탐색 트리는 입력값과 트리 노드의 값의 크기를 비교하고 있습니다. 왜 그런 것일까요?

	// 이진 탐색 트리 안에 해당 값이 포함되어 있는지 확인하는 메서드를 만듭니다.
  contains(value) {
		// TODO: 값이 포함되어 있다면 true를 반환하세요.
    if (this.value===value) {
      return true;
    }
		// 입력값을 기준으로 현재 노드의 값보다 작은지 판별하는 조건문이 있어야 합니다.
    if (value < this.value) {
      if(this.left!==null && this.left.contains(value)){
        return true;
      }
			// TODO: 현재 노드의 왼쪽이 비어 있지 않고, 노드의 값이 입력값과 일치하면 true를 반환합니다.
			
			// TODO:일치하지 않다면 왼쪽 노드로 이동하여 다시 탐색합니다. 

    }
		// 입력값을 기준으로 현재 노드의 값보다 큰지 판별하는 조건문이 있어야 합니다.
    if (value > this.value) {
      if(this.right !== null && this.right.contains(value)){
        return true;
      }
			// TODO: 현재 노드의 오른쪽이 비어 있지 않고, 노드의 값이 입력값과 일치하면 true를 반환합니다.
			
			// TODO:일치하지 않다면 오른쪽 노드로 이동하여 다시 탐색합니다. 

    }
    return false;
		// 없다면 false를 반환합니다.
  }

	/*
	트리의 순회에 대해 구현을 합니다.
  지금 만드려고 하는 이 순회 메서드는 단지 순회만 하는 것이 아닌, 함수를 매개변수로 받아 콜백 함수에 값을 적용시킨 것을 순회해야 합니다.
  전위 순회를 통해 어떻게 탐색하는지 이해를 한다면 중위와 후위 순회는 쉽게 다가올 것입니다.
	*/

	// 이진 탐색 트리를 전위 순회하는 메서드를 만듭니다.
  preorder(callback) {
		callback(this.value);
    if (this.left) {
      this.left.preorder(callback)
    };
    if (this.right) {
      this.right.preorder(callback)
    };
  }

	// 이진 탐색 트리를 중위 순회하는 메서드를 만듭니다.
  inorder(callback) {
    if (this.left){
      this.left.inorder(callback)
    }
    callback(this.value);
    if(this.right){
      this.right.inorder(callback)
    }
		//TODO: 전위 순회를 바탕으로 중위 순회를 구현하세요.
  }

	// 이진 탐색 트리를 후위 순회하는 메서드를 만듭니다.
  postorder(callback) {
    if(this.left){
      this.left.postorder(callback)
    }
    if(this.right){
      this.right.postorder(callback)
    }
    callback(this.value)
		//TODO: 전위 순회를 바탕으로 후위 순회를 구현하세요.
  }

}

• 다른 페어분의 contains 구현방법

  contains(value) {
		// TODO: 값이 포함되어 있다면 true를 반환하세요.
    if (this.value === value) {
      return true;
    }
    if (value < this.value && this.left!==null) {
      return this.left.contains(value)
    }
    if (value > this.value && this.right !== null ) {
      return this.right.contains(value)
    }
  return false

 }

• 레퍼런스코드에서는 return 값을 보자면 이중부정으로 boolean값으로 만들었다!!
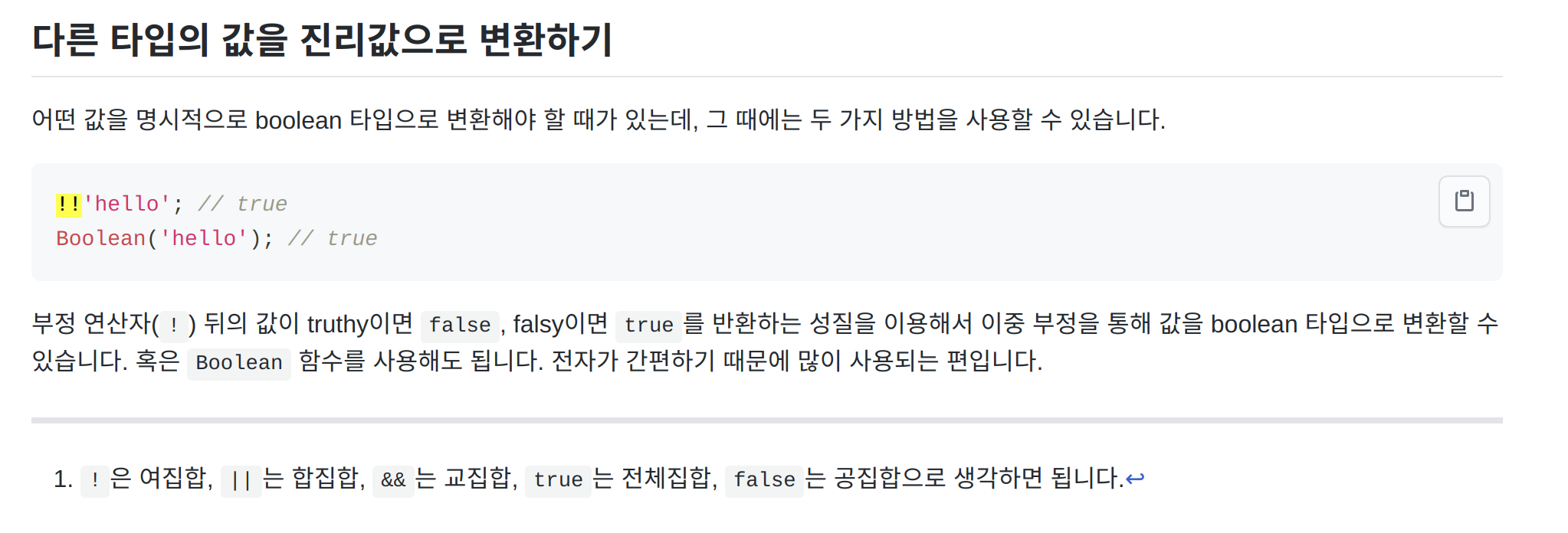
  • 다른타입의 값을 (!! 이중부정 ) 으로 "bollean"으로 만들수 있어!!
    

  contains(value) {
    // 찾는 value값이 노드의 value와 일치한다면, true를 리턴합니다.
    if (value === this.value) {
      return true;
    }
    // 찾는 value값이 노드의 value 보다 작다면, 왼쪽에서 contains의 재귀를 진행합니다.
    if (value < this.value) {
      return !!(this.left && this.left.contains(value)); 
    }
    // 찾는 value값이 노드의 value 보다 크다면, 오른쪽에서 contains의 재귀를 진행합니다.
    if (value > this.value) {
      return !!(this.right && this.right.contains(value));
    }
  }

• 즉 (1) (2)은 같다.

(1)

 if (value < this.value) {
      return !!(this.left && this.left.contains(value)); 
 }

(2)

 if (value < this.value) {
    if(this.left!==null && this.left.contains(value)){
      return true;
  }

출처: 코드스테이츠