[DataStructure / Algorithm] AVL Tree (4)

주제: 높이 균형을 유지하는 자가 균형 트리

---

AVL Tree란?

• 이진 탐색 트리의 평균 성능은 O(log n)을 나타낸다. 하지만, 균형이 잡히지 않은 트리는 성능을 저하시킬 수 있으며 최악의 경우 O(n)까지 떨어질 수 있다. 
• 1962년 Georgy Adelson-Velsky와 Evgenii Landis가 처음으로 자가 균형 이진 트리인 AVL 트리를 고안했다. 
• AVL트리는 값이 변경됨에 따라 자동으로 트리의 균형을 잡아줘서 O(log n)의 성능을 보장할 수 있게 해준다. 

Perfect balance

• 이진 탐색 트리의 이상적인 형태로써, 완벽하게 균형 잡힌 상태이다. 
• 맨 위부터 아래까지 모든 수준의 트리가 노드로 채워진 상태를 의미한다.

'Good-enough' balance

• Perfect balance을 만드는 것이 가장 이상적이지만, 실제로는 거의 불가능하다. 
• 예를 들어, 1, 3 또는 7개의 노드가 있는 트리는 완벽하게 균형 잡힐 수 있지만, 2, 4, 5 또는 6개의 노드가 있는 트리는 맨 아래 수준의 노드가 채워지지 않기 때문에 완벽하게 균형 잡힐 수 없습니다.
• 결국 균형 잡힌 트리는 맨 아래를 레벨을 제외하고 모든 수준의 트리가 채워져 있어야 한다는 것이다.

Unbalanced

• 이진 탐색 트리가 이 상태에 있다면 균형 상태가 아니게 되므로 성능 손실을 겪게 된다. 
• 결국, 이러한 상태가 발생하였을 때 균형 잡힌 상태로 맞춰줘야 한다.

구현

• AVL 트리에서 이진 트리의 균형을 유지하기 위해서는 트리의 균형을 측정하는 방법이 필요하다. 
• AVL 트리는 각 노드에 높이 속성을 사용하여 이를 달성할 수 있는데, 트리에서 노드의 높이란 현재 노드에서 가장 먼 리프 노드까지의 최장 거리를 의미한다.
• 각 노드의 자식 노드의 상대적인 높이를 사용하여 해당 노드가 균형 잡혀 있는지를 확인할 수 있다. 각 노드의 왼쪽 및 오른쪽 자식의 높이 차이는 최대 1이하여야 하며, 이 숫자를 균형 인수(balance factor)라고 한다.
• balance factor가 2또는 -2 이상이면 균형 잡히지 않은 트리이다. 
• 그렇지만, rotation(회전) 활동을 해서 balance factor를 1또는 -1이하로 낮출 수 있다.
  

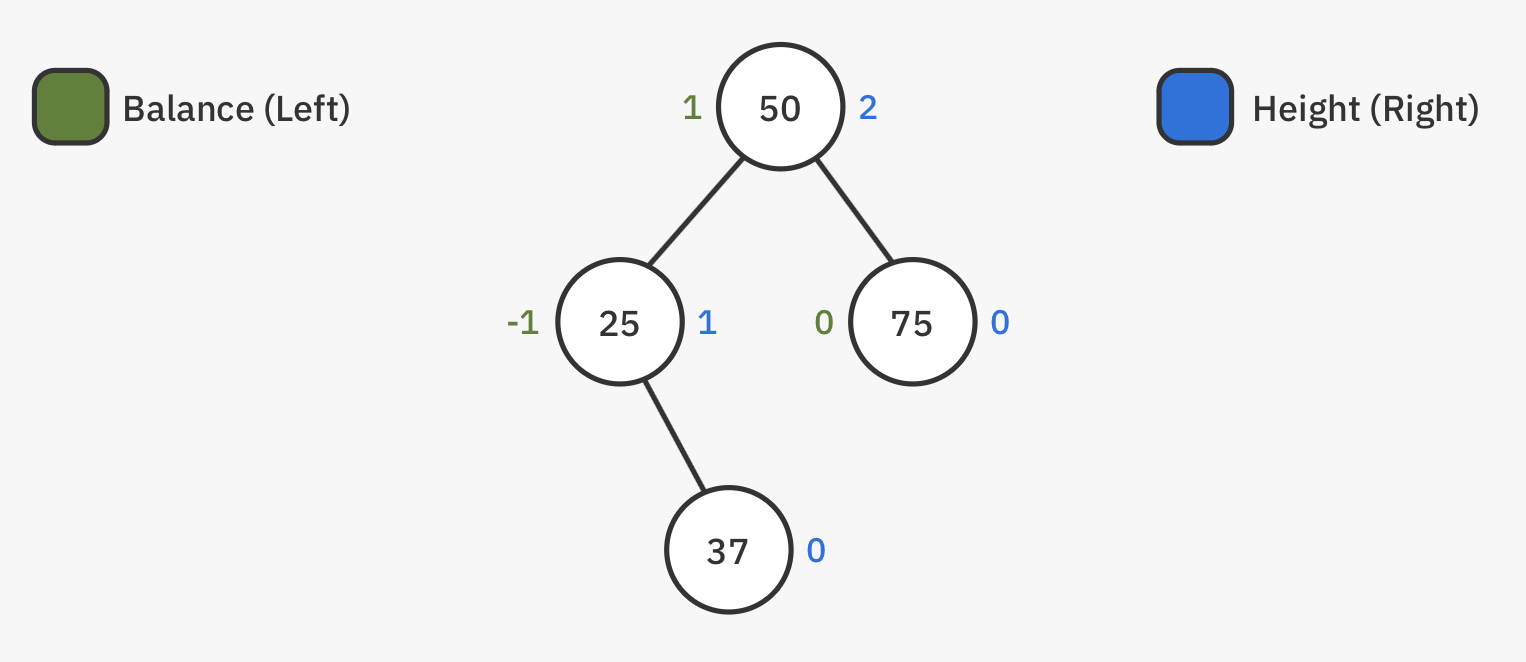
  > AVL Tree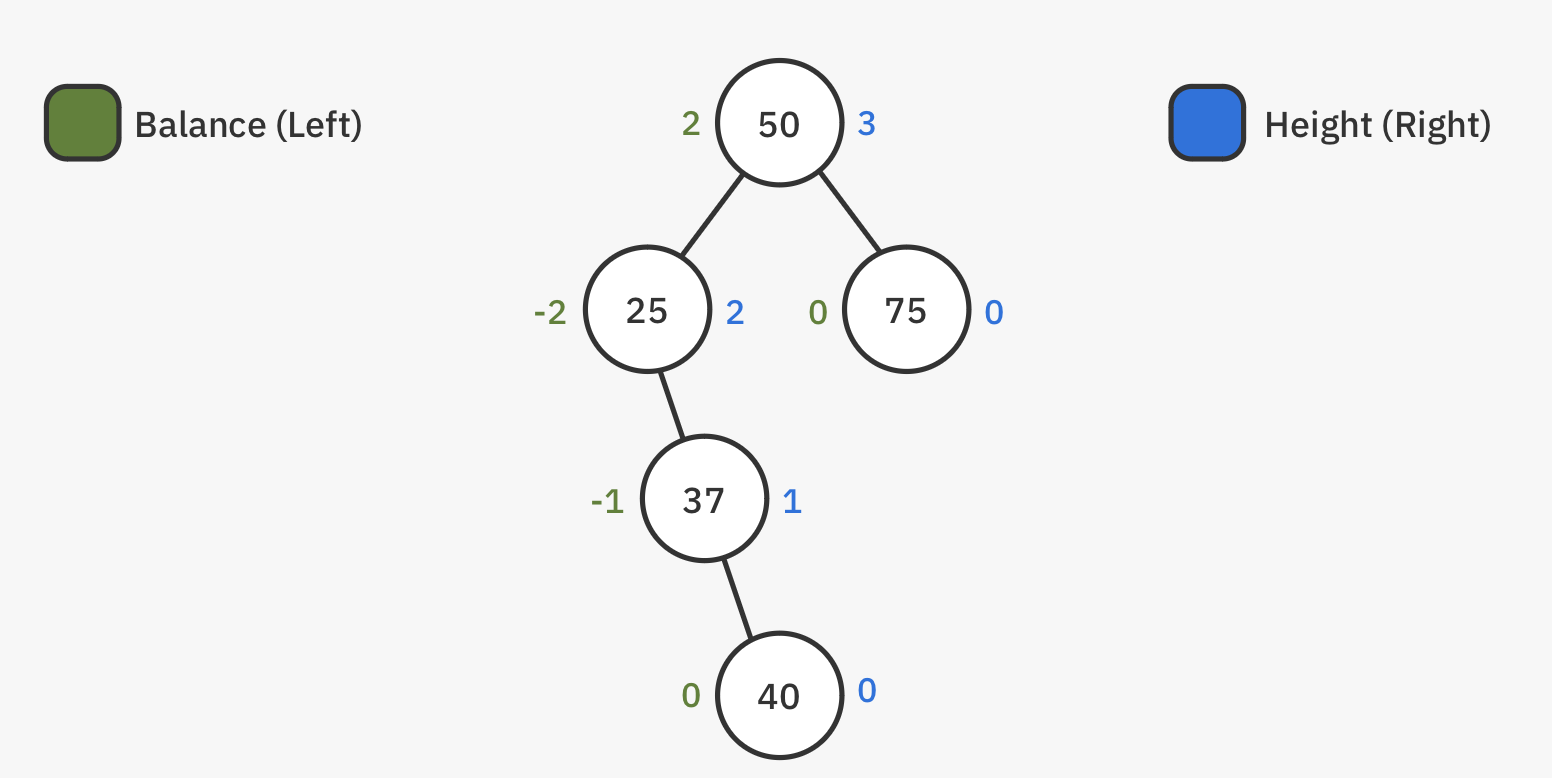

  

  > Unbalanced Tree

public class AVLNode<Element> { 
	public var value: Element 
	public var leftChild: AVLNode? 
	public var rightChlid: AVLNode? 
    // root가 가장 높음, 기본값을 0으로 반영하고 child가 생기면 
   	// child의 root node height을 변경해주는 방식
	public var height = 0 
	
    /// 2 or -2 이상일 경우 unbalanced tree
    /// 최초 child가 없으면 0
    /// left child가 생겼을 시 1
    /// right child가 생겼을 시 -1
    /// 즉, right 쪽으로 계속 추가될 시 balanceFactor는 음수 
    //// left 쪽으로 계속 추가될 시 balanceFactor는 양수
	public var balanceFactor: Int { 
		leftHeight - rightHeight 
	}
	
	public var leftHeight: Int { 
		leftChild?.height ?? -1
	}
	
	public var rightHeight: Int { 
		rightChild?.height ?? -1
	}
	
	public init(value: Element) { 
		self.value = value 
	}
}

extension AVLNode: CustomStringConvertible {
  
  public var description: String {
    diagram(for: self)
  }
  
  private func diagram(for node: AVLNode?,
                       _ top: String = "",
                       _ root: String = "",
                       _ bottom: String = "") -> String {
    guard let node = node else {
      return root + "nil\n"
    }
    if node.leftChild == nil && node.rightChild == nil {
      return root + "\(node.value)\n"
    }
    return diagram(for: node.rightChild, top + " ", top + "┌──", top + "│ ")
      + root + "\(node.value)\n"
      + diagram(for: node.leftChild, bottom + "│ ", bottom + "└──", bottom + " ")
  }
}

public struct AVLTree<Element: Comparable> { 
	public private(set) var root: AVLNode<Element>? 
	
	public init() { }
}

extension AVLTree: CustomStringConvertible { 
	public var description: String { 
		guard let root = root else { return "Empty Tree"}
		return String(describing : root)
	}
}

AVL tree Rotation Operation

• AVL트리에서의 삽입, 삭제 과정은 이진 탐색 트리에서의 삽입, 삭제 과정과 같다. 추가적으로 AVL트리는 삽입, 삭제 후 balance factor에 따라 트리를 재조정하는 과정이 추가되어야 한다.

유형	설명	방식
RR Problem	노드 N이 A의 오른쪽 서브 트리의 오른쪽 서브 트리에 삽입되는 경우	A를 기준으로 한번의 반 시계 방향 회전
LL Problem	노드 N이 A의 읜쪽 서브 트리의 왼쪽 서브 트리에 삽입되는 경우	A를 기준으로 한번의 시계 방향 회전
RL Problem	노드 N이 A의 오른쪽 서브 트리의 왼쪽 서브 트리에 삽입되는 경우	A의 오른쪽 자식을 기준으로 시계 방향 회전 후 A를 기준으로 반시계 방향 회전
LR Problem	노드 N이 A의 왼쪽 서브 트리의 오른쪽 서브 트리에 삽입되는 경우	A의 왼쪽 자식을 기준으로 반시계 방향 회전 후 A를 기준으로 시계 방향 회전

RR Problem(Single Left Rotation)

• 삽입 또는 삭제로 인해 노드의 오른쪽 서브트리에 불균형이 발생한 경우 사용된다.
  

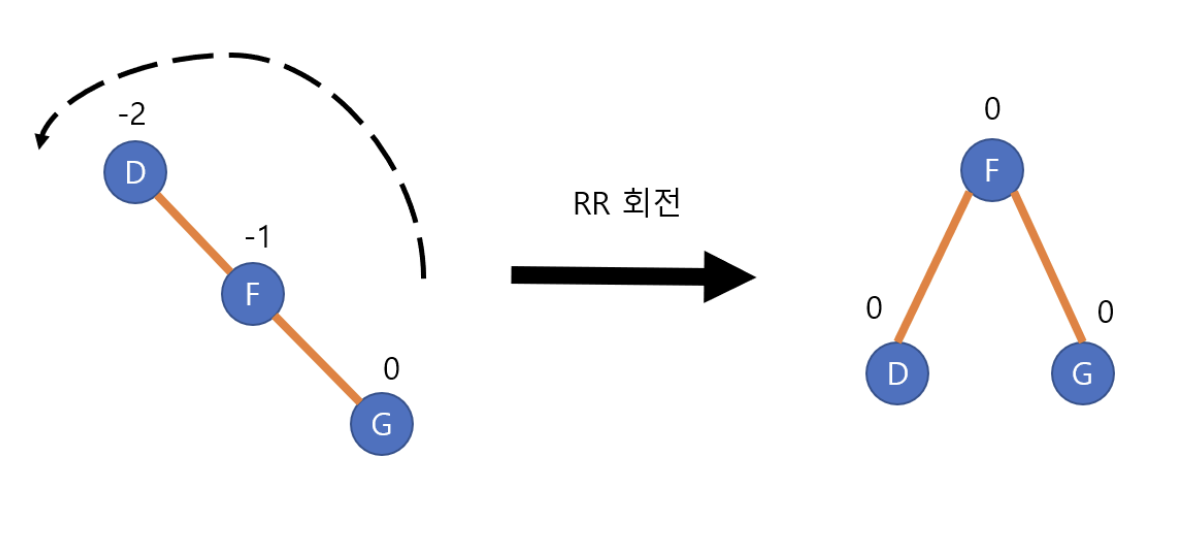
extension AVLTree { 
	private func leftRotate(_ node: AVLNode<Element>) -> AVLNode<Element> { 
		let pivot = node.rightChild!
		
		node.rightChild = pivot.leftChild
		
		pivot.leftChild = node
		
		node.height = max(node.leftHeight, node.rightHeight) + 1 
		pivot.height = max(pivot.leftHeight, pivot.rightHeight) + 1 
		
		return pivot
	}
}

LL Problem(Single Right Rotation)

• 삽입 또는 삭제로 인해 노드의 왼쪽 서브트리에 불균형이 발생한 경우 사용된다.
  

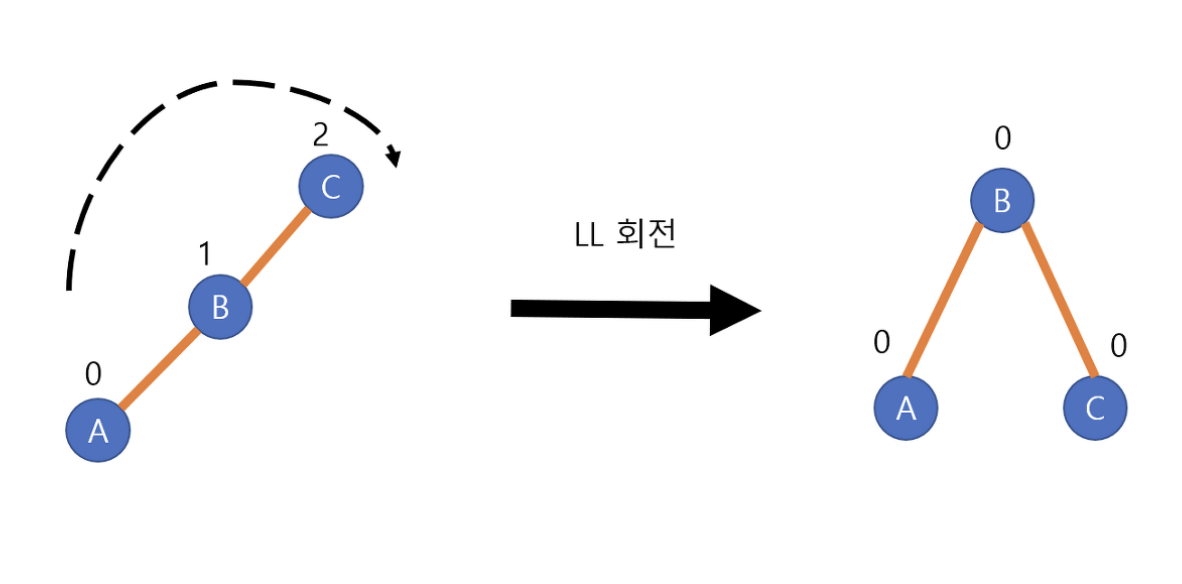
extension AVLTree { 
	private func rightRotate(_ node: AVLNode<Element>) -> AVLNode<Element> { 
		let pivot = node.leftChild! 
		
		node.leftChild = pivot.rightChild 
		
		pivot.rightChild = node 
		
		node.height = max(node.leftHeight, node.rightHeight) + 1
		pivot.height = max(pivot.leftHeight, pivot.rightHeight) + 1
		
		return pivot
	}
}

RL Problem(Right-Left Rotation or Double(Right Left) Rotation)

• 삽입 또는 삭제로 인해 노드의 오른쪽 서브트리의 왼쪽 서브트리에 불균형이 발생한 경우 사용된다. 이 회전은 오른쪽 서브트리에 대한 오른쪽 회전 후, 전체 트리에 대한 왼쪽 회전을 수행한다.
  

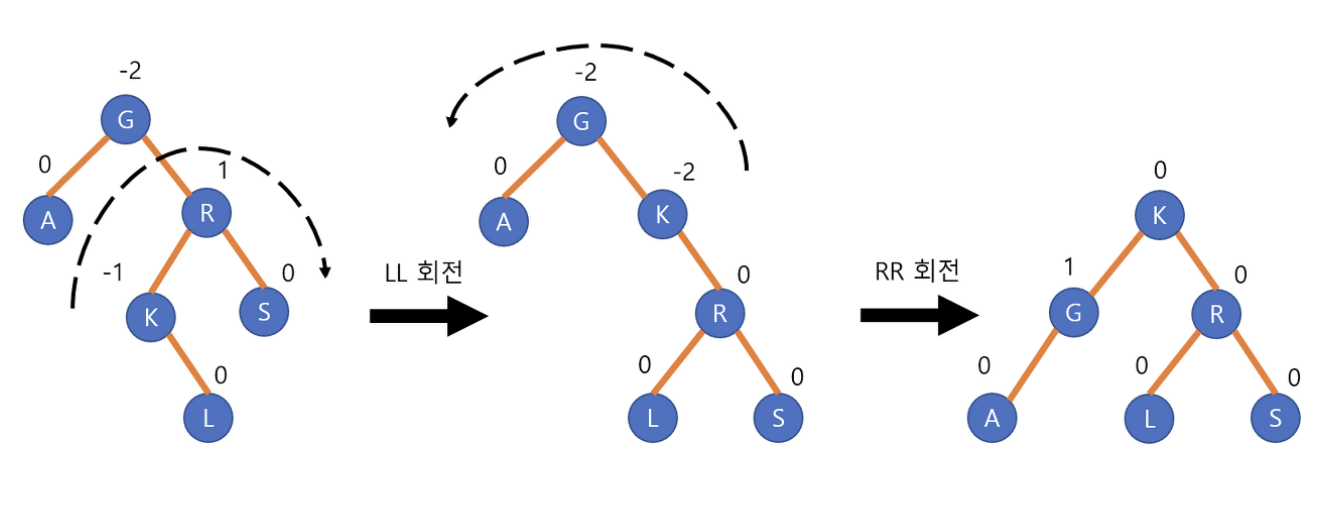
extension AVLTree { 
	private func rightLeftRotate(_ node: AVLNode<Element>) -> AVLNode<Element> { 
		guard let rightChild = node.rightChild else { 
			return node
		}
		node.rightChild = rightRotate(rightChild)
		return leftRotate(node)
	}
}

LR Problem(Left-Right Rotation or Double(Left Right) Rotation)

• 삽입 또는 삭제로 인해 노드의 왼쪽 서브트리의 오른쪽 서브트리에 불균형이 발생한 경우 사용된다. 이 회전은 왼쪽 서브트리에 대한 왼쪽 회전 후, 전체 트리에 대한 오른쪽 회전을 수행한다.
  

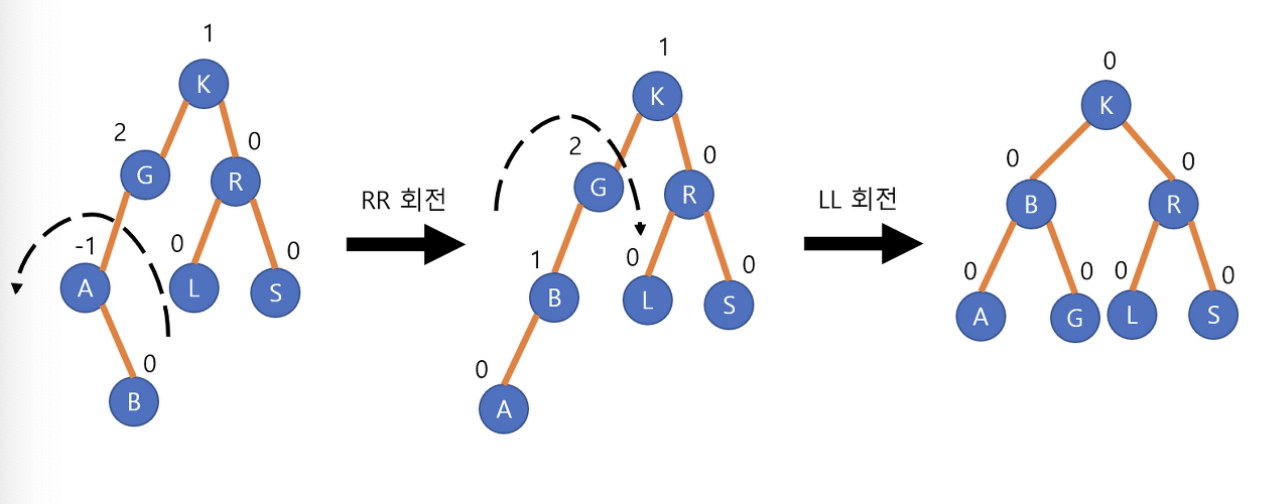
extension AVLTree { 
	private func leftRightRotate(_ node: AVLNode<Element>) -> AVLNode<Element> { 
		guard let leftChild = node.leftChild else { 
			return node
		}
		node.leftChild = leftRotate(leftChild)
		return rightRotate(node)
	}
}

Balance

• balanceFactor를 사용하여 노드가 균현을 유지해야하는지 여부를 결정하는 메서드를 설계한다.
• balanceFactor가 2인 경우 왼쪽 자식이 오른쪽 자식보다 더 많은 노드를 포함하고 있으며, 이는 LL회전 또는 LR회전을 해야 한다.
• balanceFactor가 -2인 경우 오른쪽 자식이 왼쪽 자식보다 더 많은 노드를 포함하고 있으며, 이는 RR회전 또는 RL회전을 해야 한다.

private func balanced(_ node: AVLNode<Element>) -> AVLNode<Element> { 
	switch node.balanceFactor { 
		case 2: 
			if let leftChild = node.leftChild, leftChild.balanceFactor == -1 { 
				return leftRightRotate(node)
			} else { 
				return rightRotate(node)
			}
		case -2: 
			if let rightChild = node.rightChild, rightChild.balanceFactor == 1 { 
				return rightLeftRotate(node)
			} else { 
				return leftRotate(node)
			}
		default : 
			return node
	}
}

Insertion

extension AVLTree: { 
	public mutating func insert(_ value: Element) { 
		root = insert(from: root, value: value)
	}
	
	private func insert(from node: AVLNode<Element>?, value: Element) -> AVLNode<Element> { 
		guard let node = node else { 
				return AVLNode(value: value)
		}
		if value < node.value { 
			node.leftChild = insert(from: node.leftChild, value: value)
		} else { 
			node.rifhtChild = insert(from: node.rightChild, value: value)
		}
		
		let balanceNode = balanced(node)
		balanceNode.height = max(balanceNode.leftHeight, balanceNode.rightHeight) + 1 
		return balanceNode
	}
}

removing

private extension AVLNode { 
	var min: AVLNode { 
		leftChild?.min ?? self
	}
}

extension AVLTree { 
	public mutating func remove(_ value: Element) { 
		root = remove(node: root, value: value)
	}
	
	private func remove(node: AVLNode<Element>?, value: Element) -> AVLNode<Element>? { 
		guard let node = node else { 
			return nil
		}
		
		if value == node.value { 
			if node.leftChild == nil && node.rightChild == nil { 
				return nil
			}
			if node.leftChild == nil { 
				return node.rightChild 
			}
			if node.rightChild == nil { 
				return node.leftChild 
			}
			node.value = node.rightChild!.min.value 
			node.rightChild = remove(node: node.rightChild, value: node.value)
		} else if value < node.value { 
			node.leftChild = remove(node: node.leftChild, value: value)
		} else { 
			node.rightCHild = remove(node: node.rightChild, value: value) 
		}
		
		let balancedNode = balanced(node)
		balancedNode.height = max(balancedNode.leftHeight, balancedNode.rightHeight) +  1 
		return balancedNode
	}
}

• 결과 

var tree = AVLTree<Int>()

for i in 0..<15 {
    tree.insert(i)
}
print(tree)
tree.remove(14)
print(tree)

  ┌──14
 ┌──13
 │ └──12
┌──11
│ │ ┌──10
│ └──9
│  └──8
7
│  ┌──6
│ ┌──5
│ │ └──4
└──3
 │ ┌──2
 └──1
  └──0

  ┌──nil
 ┌──13
 │ └──12
┌──11
│ │ ┌──10
│ └──9
│  └──8
7
│  ┌──6
│ ┌──5
│ │ └──4
└──3
 │ ┌──2
 └──1
  └──0

출처(참고문헌)

• https://www.kodeco.com/books/data-structures-algorithms-in-swift/v4.0/chapters/16-avl-trees
• https://limecoding.tistory.com/118

제가 학습한 내용을 요약하여 정리한 것입니다. 내용에 오류가 있을 수 있으며, 어떠한 피드백도 감사히 받겠습니다.

감사합니다