AVL 트리의 어원

AVL 트리는 과거 소련과 이스라엘의 수학자이자 컴퓨터 과학자이자 컴퓨터 체스의 개척자인 Adelson-Velsky와 Evgenii Landis가 함께 발명한 트리이며 이름의 앞 글자를 따서 AVL 트리로 명명하였다.

Adelson-Velsky 아저씨의 모습

전에 자가 균형 이진탐색트리 중 하나인 Red-Black 트리에 대해서 알아보았다. 이번에는 또다른 자가 균형 이진탐색 트리 AVL트리에 대하여 알아보자.

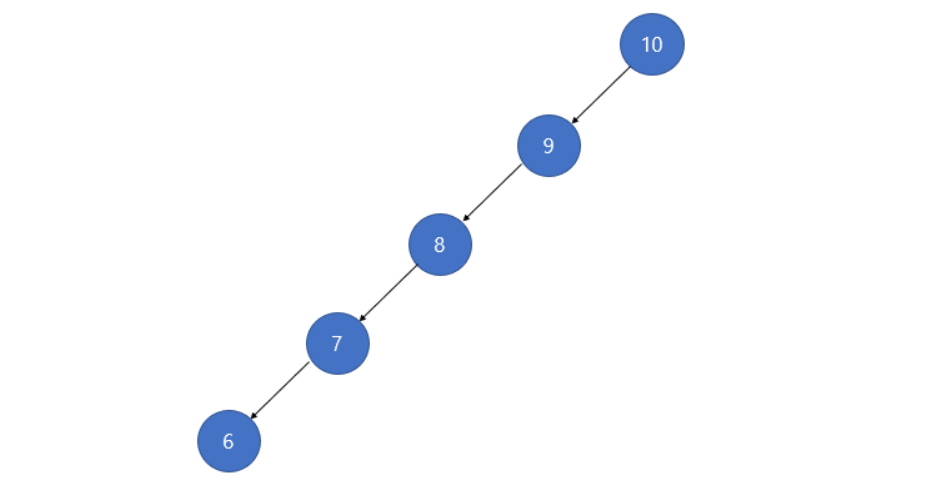
이진 탐색트리는 그림과 같이 최악의 경우인 편향트리가 될 수 있다. 10, 9, 8, 7, 6을 순서대로 삽인한다고 할 때 이렇게 worst case가 만들어진다. 위와 같은 방식으로 트리가 존재할 때 우리가 수자 6을 찾는다면 루트 노드부터 6까지 노드의 개수만큼 이동을 해야한다. 이 때 시간 복잡도는 O(n)이다. 즉 성능이 매우 나빠지게 된다. 이러한 단점을 극복하기 위해 만들어진 자료구조가 AVL 트리이다.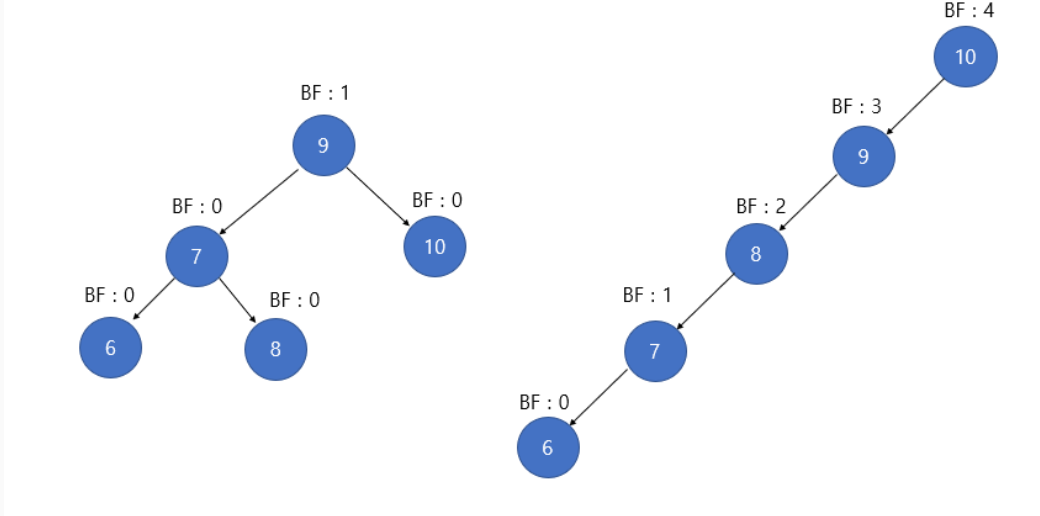
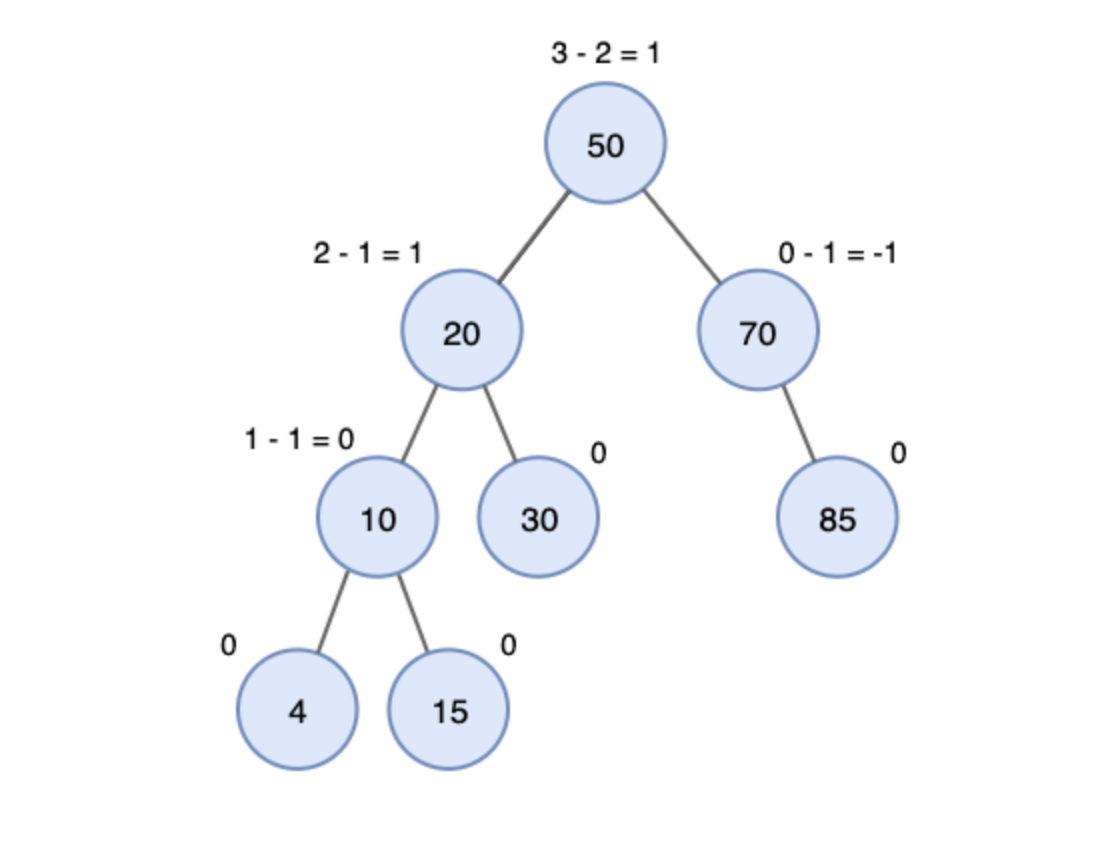
다음은 첫 번째 그림을 AVL 트리로 재구성 한 것이다. 지금부터 어떻게 재구성하는지 알아보도록 하자.

AVL 트리의 특성

1. 이진 탐색 트리의 속성을 가진다.
2. 왼쪽, 오른쪽 서브 트리의 높이 차이가 최대 1이다.
3. 높이 차이가 1보다 커지면 회전(Rotation)을 통해 균형을 맞춰 높이 차이를 줄인다.
4. 삽입, 검색, 삭제의 시간 복잡도가 O(log N)이다. (N : 노드의 개수)

AVL 트리의 특성을 알아보았다. 그 다음 회전 과정을 알아보기 전에 AVL Balance Factor에 대하여 알아보자

Balance Factor

📌 AVL트리는 균형이 무너졌는지에 대해 판단할 때 Balance Factor라는 것을 활용한다. 공식은 다음과 같다.
📌BF(K) = K의 왼쪽 서브트리의 높이 - K의 오른쪽 서브트리의 높이
AVL트리는 모든 노드의 BF가 -1,0,1 중 하나여야 한다. 만약 이를 벗어나면 균형이 깨졌다는 것을 의미하고, 이때 회전이 필요한 것이다.

회전에 대해 설명하기 전에 T1, T2..등은 서브트리를 의미하고, 회전의 기준은 z노드라고 가정하자.

How to Rotation?

우회전(Right Rotation)

📌y노드의 오른쪽 자식 노드를 z노드로 변경한다.
📌z노드 왼쪽 자식 노드를 y노드의 오른쪽 서브트리(T2)로 변경한다.

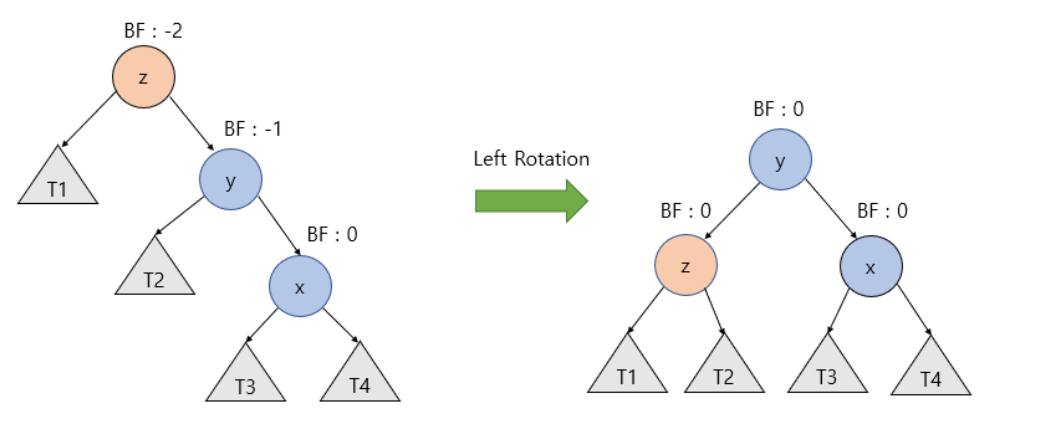
좌회전(Left Rotation)

📌 y노드의 왼쪽 자식 노드를 z노드로 변경한다.
📌 z노드 오른쪽 자식노드를 y노드의 왼쪽 서브트리(T2)로 변경한다.

이렇게 우회전, 좌회전 회전 방법에 대하여 알아보았다. 다음은 균형이 무너진 4가지의 case와 각각의 해결법에 대하여 알아보자.

Unbalanced case

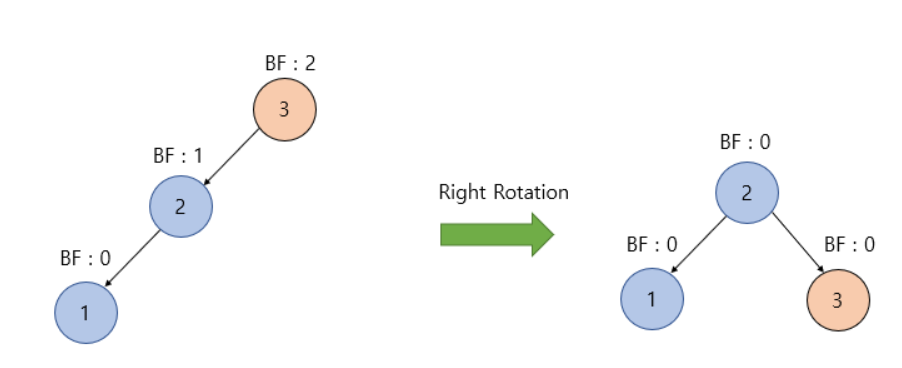
LL(Left Left) Case

위 그림처럼 BF가 -1~1을 벗어난 노드를 기준으로 왼쪽, 왼쪽 노드가 존재한다면 LL Case이다. 이때 해당 노드를 기준으로 우회전을 적용하면 불균형이 해소된다.

RR(Right Right) Case

위 그림처럼 BF가 -1~1을 벗어난 노드를 기준으로 오른쪽, 오른쪽 노드가 존재한다면 RR Case이다.
이때 해당 노드를 기준으로 좌회전을 적용하면 불균형이 해소된다.

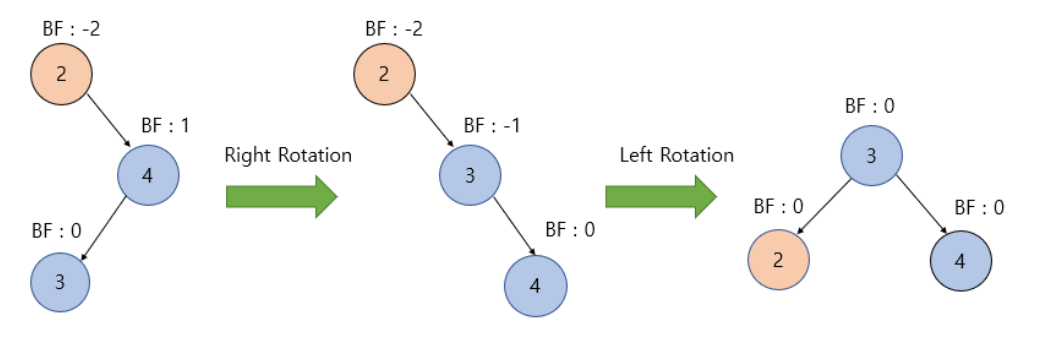
LR(Left Right) Case

이때 먼저 BF에 이상이 있는 노드(값이 4인노드)의 왼쪽 자식노드(값이 2인 노드)를 기준으로 좌회전을 진행한다.
이후 BF에 이상이 있는 노드(값이 4인 노드)를 기준으로 우회전을 진행하면 불균형이 해소된다.

RL(Right Left) Case

위 그림처럼 BF가 -1~1을 벗어난 노드를 기준으로 오른쪽(Right), 왼쪽(Left) 노드가 존재한다면 RL Case이다.
이때 먼저 BF에 이상이 있는 노드(값이 4인노드)의 오른쪽 자식노드(값이 4인 노드)를 기준으로 우회전을 진행한다.
이후 BF에 이상이 있는 노드(값이 4인 노드)를 기준으로 좌회전을 진행하면 불균형이 해소된다.

AVL 트리 시뮬레이터

설명만 들으면 어려우니 시뮬레이터를 이용하여 이해해보자
https://www.cs.usfca.edu/~galles/visualization/AVLtree.html

감사합니다.

자료 출처
: https://code-lab1.tistory.com/61?category=1213002
: https://www.chessprogramming.org/File:Adelson-Velsky-G.Moscow-1980.jpg