
지금까지 비대칭 암호 알고리즘에 대해 알아보았습니다. 비대칭 암호 알고리즘들은 형태는 달라도 모두 비밀통로 일방향 함수를 통해 암호화와 복호화를 할 수 있었습니다. 대칭 암호 알고리즘과 비대칭 암호 알고리즘을 모두 양방향 암호 시스템이라고 합니다.
해시 함수는 대표적인 단방향 암호화입니다. 어떤 값을 해시 함수에 넣는다면 그 결과값을 다시 얻어내는 것은 불가능합니다. 이전에 살펴봤던 암호화는 복호화를 안전하게 해서 기밀성을 지켰습니다. 하지만 해시 함수는 원래 정보를 아무도 알 수 없다는 점에서 기밀성을 지킬 수가 없습니다. 그렇다면 해시 함수는 왜 쓰이는지, 어떻게 만들어지는지 알아보겠습니다.
해시 함수란
해시 함수란 임의의 길이의 평문을 정해진 길이의 해시값으로 변경하는 일방향 함수입니다. 따라서 길이가 즐어들거나 늘어날 수 있고 그에 따라 표현할 수 있는 값의 범위가 한정됩니다. 그러한 길이를 충분히 크게하지 않을 때 해시 충돌이 일어날 수 있습니다.
해시 함수는 무결성을 검증하는 것에 사용됩니다. 평문의 극히 작은 부분만 바꾸더라도 눈사태 효과 (Avalanche Effect)에 의하여 최종 결과값은 큰 차이를 보이게 됩니다. 따라서 위조, 변조가 불가능하게끔 하는 것에 그 의의를 두고 있습니다. 내용이 공개되는 것은 상관없지만 그 무결성이 필요하다면 해시 함수를 사용할 수 있습니다. 만약 양방향 암호화와 해시 함수를 같이 이용한다면 기밀성과 무결성을 모두 지킬 수 있을 것입니다.
Avalanche Effect 확인
파이썬에 있는 hashlib를 사용하면 SHA3-512 해시 함수를 사용할 수 있습니다.
import hashlib
def hamming_distance_for_hex(x, y):
bin_x = format(int(x, 16), "04b")
bin_y = format(int(y, 16), "04b")
result = 0
for i in range(4):
if bin_x[i] != bin_y[i]:
result += 1
return result
def get_hamming_distance(x, y):
res = 0
for i, j in zip(x, y):
res = hamming_distance_for_hex(i, j) + res
return res
def get_hash(m):
s = hashlib.sha3_512()
s.update(m)
return s.hexdigest()
f = open("output.txt", 'w')
m1 = bytes(1024)
hash1 = get_hash(m1)
f.write("m1's hash value : " + hash1 + "\n")
m2 = bytearray(m1[:])
m2[0] = 128
m2 = bytes(m2)
hash2 = get_hash(m2)
f.write("m2's hash value : " + hash2 + "\n")
m3 = bytearray(m1[:])
m3[1023] = 1
m3 = bytes(m3)
hash3 = get_hash(m3)
f.write("m3's hash value : " + hash3 + "\n")
res1 = get_hamming_distance(hash1, hash2)
res2 = get_hamming_distance(hash1, hash3)
res3 = get_hamming_distance(hash2, hash3)
f.write("hamming distance between m1's hash value and m2's : " + str(res1) + "\n")
f.write("hamming distance between m1's hash value and m3's : " + str(res2) + "\n")
f.write("hamming distance between m2's hash value and m3's : " + str(res3) + "\n")
f.close()결과
m1's hash value : befb5811dc48581722cbbf6d72ebf780722f0c7aca02366ded4562608bbb1e1fe7ee518a28426e51bab6d7c0c057bbd3e1cf6fc13d5947b71667f3a78b048b00 m2's hash value : 6027e3332ec3b321022c9fa90aaa1ddbf29389192e8b5bec2522f4277c2595264f6e85b3b93b75163b05a191d48e247d41ec6f4c18bbe36c6a2b656167a097fc m3's hash value : e8b0b9c85654582d6186f800bd2be651e8fa9b406e1378d77168ae77f5711744800e2cce47f4735a73ff9825996a118d46a9320068c95c22500b841a480200c4 hamming distance between m1's hash value and m2's : 247 hamming distance between m1's hash value and m3's : 254 hamming distance between m2's hash value and m3's : 249
해시 함수의 요구사항
해시 함수 는 다음 요구사항들을 지켜야 합니다.
- 효율적인 계산
해시 함수의 결과값을 얻는 과정은 복잡한 계산으로 이루어져서는 안됩니다. - 보안의 특성
- 제 1 역상 저항성 (Preimage resistance)
해시값을 이용해 원래 값을 알 수 없어야 합니다. 수식으로 표현하면 해시 함수의 결과값 가 주어졌을 때, 인 를 찾아낼 수 없다는 성질이 됩니다. 이를 One-wayness 라고도 합니다. - 제 2 역상 저항성 (2nd preimage resistance)
여러 값을 넣어서 같은 해시값이 나오는 값을 찾아내는 것이 불가능해야 합니다. 수식으로 표현하면 가 있을 때, 인 를 찾을 수 없다는 성질이 됩니다. 이를 Weak collison resistance 라고도 합니다. - 충돌 저항성 (Collision resistance)
제 2 역상 저항성에서 좀 더 일반적으로 해시 함수의 결과값이 같은 두 값을 알아낼 수 없어야 합니다. 을 만족하는 두 쌍의 입력값 을 찾을 수 없다고 표현할 수 있습니다. 이를 Strong collision resistance 라고도 합니다.
- 제 1 역상 저항성 (Preimage resistance)
해시 함수의 설계
해시 함수의 초기 형태로 MD(Message Digest) 함수가 있습니다. MD 함수는 간단하게 정리하면 블록 암호에서 영향을 받아 암호화를 반복해서 진행하는 형태라고 볼 수 있습니다. 그러나 현재 MD2에서 시작해 개선을 거듭한 MD4, MD5 모두 결함이 있는 것으로 밝혀졌습니다.
생일 공격(Birthday attack)은 해시 함수의 충돌을 찾아내는 공격입니다. 이 공격은 생일 문제를 기반으로 하고 있습니다. 생일 문제란 사람이 임의로 모였을 때 생일이 같은 두 명이 존재할 확률을 구하는 문제입니다. 간단하게 생각해보면 비둘기집의 원리에 의해 366명이 모인다면 반드시 생일이 겹치는 사람이 존재할 것입니다. 계산해보면 놀랍게도 23명 이상 모인다면 생일이 같은 두 명이 존재할 확률이 이상입니다.
해시 함수의 결과값이 개 존재한다면 개의 임의의 입력값을 선택해 해시 충돌을 찾을 확률은 다음과 같습니다.
컴퓨팅 성능이 발전할수록 해시 함수의 충돌 공격을 성공시킬 수 있는 범위도 커지기 때문에 해시 함수 또한 개선을 거듭하고 있습니다.
MD5의 취약점을 개선하기 위해 만들어진 대표적인 해시 함수인 SHA(Secure Hash Algorithm) 또한 SHA-0, SHA-1, SHA-2, SHA-3까지 발전했습니다. 2015년까지 90% 이상의 사이트가 SHA-1을 사용했으나 구글에 의해 2017년 SHA-1 전체의 해시 충돌이 밝혀졌고 실제 충돌이 발생한 다른 내용의 PDF 파일 2개를 공개하기까지 했습니다. 그러한 결함을 해결하기 위해 제안된 SHA-2 또한 SHA-1과 알고리즘의 기본 동작을 공유하기 때문에 새로운 알고리즘의 필요성이 높아졌고 현재는 SHA-3 표준으로 Keccak이 선정되어 쓰이고 있습니다.
해시 함수의 알고리즘은 각각 다르긴 하지만 일부 알고리즘에 대해 알아보겠습니다.
MD5
MD5는 임의의 길이의 입력을 받아 고정 128비트의 출력값을 냅니다.

위 그림은 MD5의 단일 연산으로 MD5는 위 연산을 64번 실행합니다.
- 입력받은 평문의 길이가 (512의 배수 - 64) 비트가 되도록 패딩(채워 넣기)합니다.
- 1번 과정의 64비트를 채웁니다. 이 때 평문의 길이가 보다 클 경우 작은 64비트만 사용합니다. 패딩이 완료된 메시지를 16 워드 단위 (1 워드는 32비트로 봅니다)로 M[0, ... , N - 1]에 할당시킵니다.
- MD 버퍼를 초기화 시킵니다. 초기 형태는 다음과 같습니다.
word A: 01 23 45 67 word B: 89 AB CD EF word C: FE DC BA 98 word D: 76 54 32 10
- 16 워드 블록 단위로 압축을 수행합니다. 압축은 4라운드로 이루어져 있습니다. 각 라운드는 비선형 함수 , 모듈러 덧셈, 레프트 로테이션에 기반한 16개의 연산으로 이루어져 있습니다. 함수 의 형태는 다음과 같습니다.
이러한 형태의 함수로 3개의 32비트 를 입력하여 32비트 워드가 생성되도록 정의합니다. 각 라운드는 현재의 512비트 블록과 3번에서 정의한 MD 버퍼 A, B, C, D, 입력 평문의 번째의 32비트 내용의 입력으로 처리됩니다. 입력 메시지의 번째의 32비트 내용은 총 64개로 각각의 라운드마다 입력됩니다.
5. 4번 과정을 통해 얻은 A, B, C, D의 값을 연결합니다.
SHA-1
SHA-1은 임의의 길이의 입력을 받아 고정 160비트의 출력값을 냅니다.
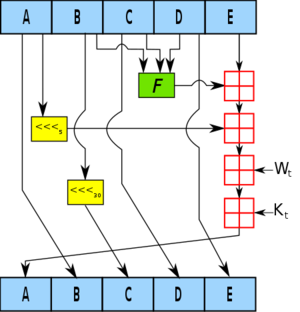
위 그림은 SHA-1 함수가 단일 블록을 처리하는 과정입니다. 입력받은 평문의 길이를 512비트의 배수로 만들기 위해 패딩 처리를 한 후 512비트로 쪼갰을 때 512비트 하나를 한개의 블록으로 봅니다.
패딩이 끝난 뒤 하나의 블록에 대해 80개의 값 부터 를 계산합니다.
는 의 결과값을 좌측으로 1회 회전한 결과값입니다.
좌측 회전(Cyclic Left Shift, CLS)은 모든 비트를 왼쪽으로 밀고 가장 왼쪽 비트는 맨 오른쪽에 붙이는 연산입니다.
그 후 입력 블록에 대해 80단계의 처리를 거칩니다. 이 처리에 대해서는 생략하겠습니다.
Keccak
Keccak은 NIST가 승인한 SHA-3 표준 해시 알고리즘입니다. 스펀지 구조로 이루어져 스펀지 함수라고도 합니다.
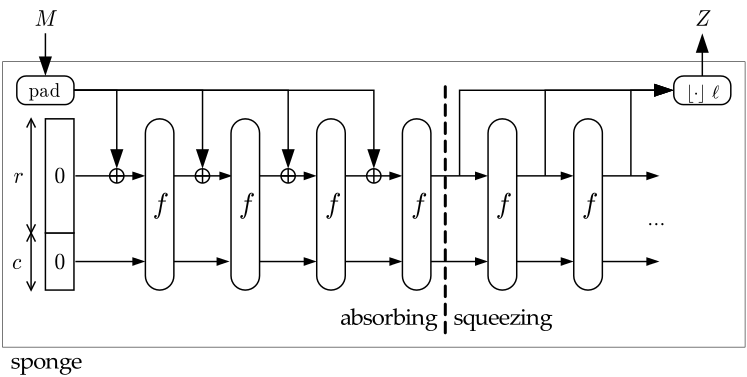
스펀지 함수는 흡수 단계와 추출 단계로 구분됩니다. 간단하게 데이터를 모으고 짜내는 단계로 볼 수 있습니다. 은 rate, 는 capacity를 나타냅니다. 함수는 값을 사용합니다.
- 흡수 단계에서는 데이터의 앞쪽 개의 비트를 모아서 XOR 연산과 함수 에 대입하는 연산을 진행합니다.
- 추출 단계에서는 데이터의 앞쪽 개의 비트를 결과값으로 모읍니다.
Keccak에서는 일반적인 공격에 대해 Hermetic sponge strategy를 따르도록 설계되어 있습니다. Hermetic sponge strategy는 다음과 같습니다.
- 구체적인 스펀지 함수를 정합니다.
- 그 함수의 보안 레벨을 로 결정할 수 있어야 합니다.
보안 레벨이 이라는 것은 충돌 공격에 대해 내성을 가져야한다는 뜻입니다. Keccak은 이 두 가지 특성을 만족하도록 설계되었습니다.
Keccak은 앞서 살펴본 해시 함수와 같이 블록 암호와 비슷한 형태로 구성됩니다. Keccak은 의 3차원 배열 형태를 쓰고 있습니다.
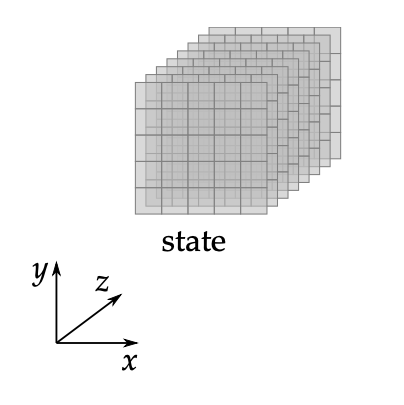
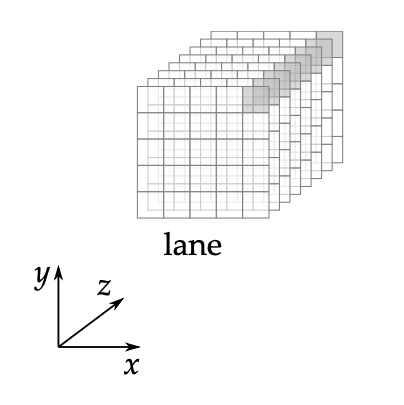
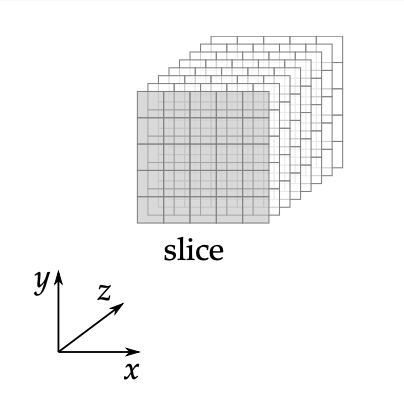
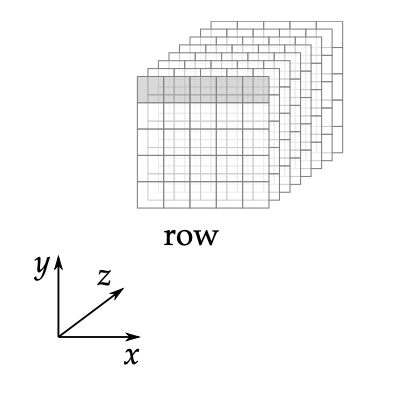
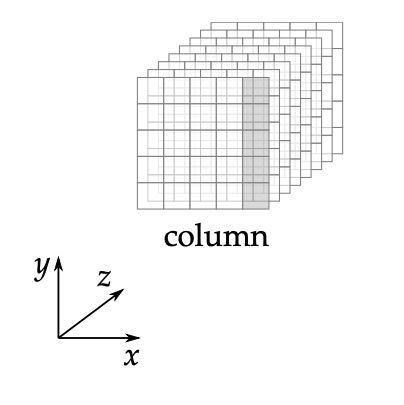
하나의 3차원 배열을 state, , 축 값을 지정한 z축 방향의 1차원 배열을 lane, 축 값을 지정한 2차원 배열을 slice, , 축 값을 지정한 1차원 배열을 row, , 축 값을 지정한 1차원 배열을 column이라고 합니다.
Keccak의 연산은 총 5가지가 있습니다.
처음부터 이러한 연산이 정의되어있지는 않았습니다. 변화가 있었는데 그것에 대해 설명하겠습니다.
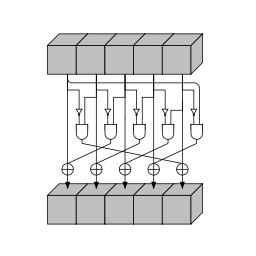
Keccak의 비선형 매핑 연산을 라고 합니다. 연산을 다음과 같이 정의합니다. 이 연산은 어떤 특정 정보에 대해 독립적으로 평행하게 연산 가능하며 정보가 전달될 수 있습니다.
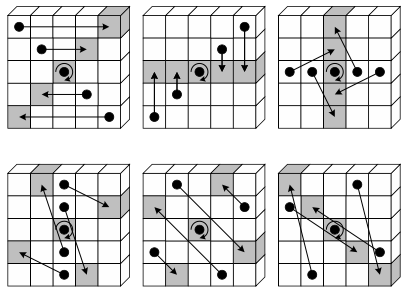
연산은 다음과 같이 정의됩니다.
연산은 slice에서 분산을 위한 연산입니다. lane에서 비트 회전을 다음과 같은 연산으로 진행합니다.
연산은 대칭성을 깨트리기 위한 연산입니다.
라운드 상수(Round constant)는 다음과 같이 정의됩니다.
는 다음과 같이 정의됩니다.
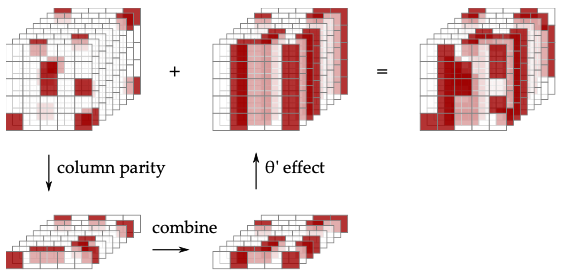
Keccak이 만들어 질 때 처음 라운드 함수는 의 형태였습니다. 그러나 이 연산을 진행할 경우 아래와 같은 문제가 발생했습니다.
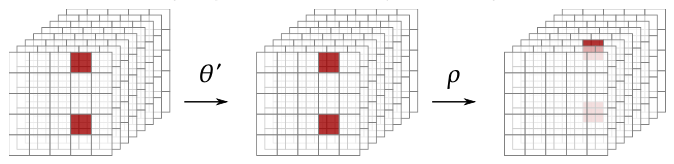
이것을 마트료시카 성질(Matryoshka property)이라고 합니다. 축에 대해 주기성을 가지게 되어 새로운 연산을 필요로 하게 되었습니다.
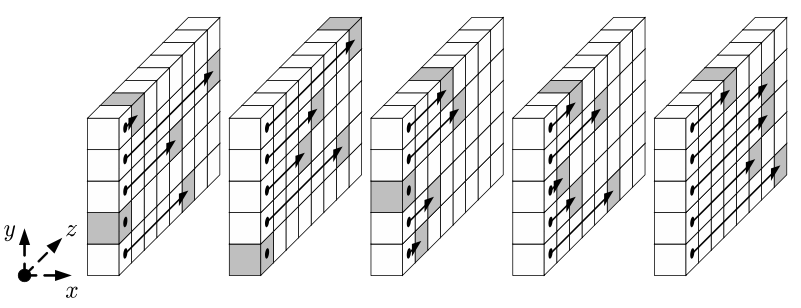
그렇게 새로 도입된 연산이 연산 입니다. 연산은 수직/수평에 대해 정렬되는 것을 막는 연산입니다.
이 두번째 시도에서 라운드 함수는 형태를 가지게 되었습니다. 이후 실험을 통해 연산이 layer를 섞는 과정에 도움을 적게 준다는 것을 확인하고 연산으로 변경하게 됩니다. 연산은 다음과 같이 정의됩니다.
최종적인 라운드 함수의 형태는 형태가 됩니다.
Keccak은 총 12 + 2 개의 라운드를 거칩니다.
해시 함수의 활용
해시 함수는 무결성을 증명하는 많은 분야에서 사용됩니다.
대표적으로 비밀번호의 경우 해시값으로 서버에 저장한다면 서버에 저장된 모든 내용이 유출되더라도 원래 비밀번호를 알아낼 수는 없습니다. 로그인 시도가 있을 때마다 입력한 비밀번호를 해시 함수를 통해 해시값을 얻어낸 후 서버에 저장된 해시값과 비교한다면 비밀번호를 검증할 수 있습니다.
현재는 디지털 서명, 전자투표, 전자 상거래 등 민감한 정보의 무결성을 검증할 때 사용합니다. 한국의 인터넷뱅킹, 비트코인의 작업증명에 SHA-256이 쓰이고 있으며 이더리움의 작업증명에도 keccak256이 사용되었습니다.
