[암호학] 8. 영지식 증명 (2)

Soowon Jeong·2022년 2월 4일

암호학

목록 보기

9/9

이 글은 Zcash의 What are zk-SNARKs?를 참고하여 작성했습니다.

zk-SNARK

zk-SNARKs는 'zero-knowledge Succinct Non-interactive Argument of Knowledge'의 약자로, 기존의 영지식 증명을 좀 더 간결하고(succinct) 비대화 환경(non-interactive)에서 적용 가능하도록 변형한 기술입니다. 이러한 변형을 통해 실제 블록체인 환경에서 사용되고 있습니다.
zk-SNARK는 크게 증명하고자 하는 문제를 특정한 형태로 변형하는 부분과 변환된 문제를 이용해 실제 증명을 진행하는 부분으로 나뉩니다.

문제 변형

Arithmetic Circuit

변환 과정의 첫 단계는 검증 함수의 계산과정을 산술 회로(Arithmetic Circuit)으로 표현하는 것입니다. 산술 회로란 여러 산술 연산을 수행하는 회로입니다. 프로그래밍 언어의 AST처럼 가장 작은 단위인 변수와 연산자로 쪼개 수식을 표현합니다.

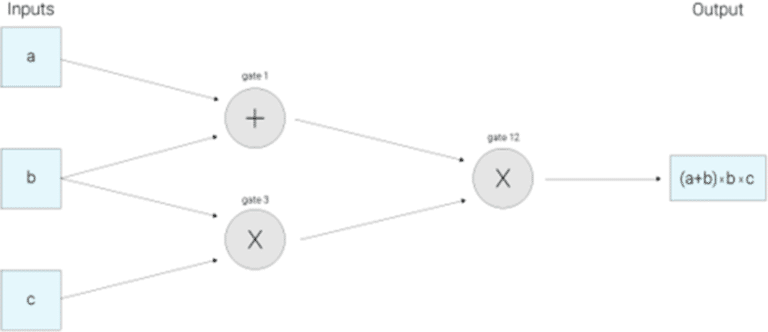
위 그림처럼 $(a + b) * b *c$ 를 $a$ , $b$ , $+$ , $c$ , $*$ 로 분리할 수 있습니다.

R1CS

다항식의 단일 산술 연산을 기준으로 한개씩 쪼갠다면 위의 다항식은 $A = a + b$ , $B = A * b$ , $C = B * c$ 로 나눠질 수 있습니다. 분할된 각각의 연산을 로직 게이트라고 부릅니다. 변수와 중간에 발생한 임의의 변수들은 행이 한개인 벡터로 매핑됩니다. 따라서 변수는 $(a, b, c, A, B, C)$ 라는 벡터로 볼 수 있고 이를 통해 게이트를 행렬로 표현할 수 있습니다. 각 게이트를 행렬로 표현하기 위해서 또 다른 벡터를 게이트의 개수만큼 선언합니다. 각 게이트에서 나온 변수는 순서대로 벡터에 들어갑니다. 이 때 $a$ , $b$ , $A$ , $B$ , $c$ 가 각각 벡터에 존재하는지(다항식에 존재하는지)에 따라 존재하면 1, 존재하지 않으면 0으로 표현합니다. 따라서 벡터로 표현한다면 $v_1 = (1, 1, 0, 1, 0, 0)$ , $v_2 = (0, 1, 0, 1, 1, 0)$ , $v_3 = (0, 0, 1, 0, 1, 1)$ 로 표현됩니다. 이런 행렬 그룹을 R1CS (Rank 1 Constraint System)라고 합니다. 이 과정에서 모든 값을 계산해 채워넣은 벡터를 솔루션 벡터 $s$ 라고 하는데, $v_1s + v_2s - v_3s$ 수식에 벡터 변수 값을 바꿔 넣어도 항상 0이 됩니다. 이를 이용해 검증자가 벡터들을 대입해 실제로 0이 되는지 확인하면 솔루션 $s$ 를 몰라도 $s$ 가 유효하다는 것을 알 수 있습니다. 하지만 실제로 다항식의 개수가 수천개가 넘어가는 상황에서는 이러한 연산을 각각의 다항식에 대해 모두 수행하기에는 시간이 많이 걸려 QAP라는 형태로 변환됩니다.

QAP

QAP는 Quadratic Arithmetic Program이라는 뜻으로 각 게이트별 제약사항을 임의의 게이트 변수를 통해 하나의 다항식 형태로 표현합니다. 자세하게 설명하자면 임의의 게이트 값을 변수로 대입하면 해당 게이트 값에 해당하는 R1CS 다항식이 나옵니다. 위의 예에서 게이트 변수를 순서대로 1, 2, 3이라고 하겠습니다. 임의의 QAP인 $P(x)$ 가 정의되었다면 $P(1)$ 은 첫번째 게이트의 검증식이 나오고 $P(2)$ 는 두번째 게이트, $P(3)$ 은 세번째 게이트의 검증식이 나오는 형태입니다. R1CS의 성분 벡터들을 다항식 형태로 바꾸기 위해 라그랑주 보간법을 사용합니다. 라그랑주 보간법은 특정 좌표를 지나는 다차함수를 만들 수 있습니다. 또한 유효한 P가 있다면 모든 게이트 변수가 해당 방정식의 해가 되어야하고, 목표 다항식 $T$ 를 정의한 뒤 $P$ 가 $T$ 로 나뉘는지 확인하는 것을 유효성 검증으로 볼 수 있습니다. 간단히 위의 예에서는 3개의 게이트에서 함수값이 0이 되었으므로 $T(x) = (x - 1)(x- 2)(x - 3)$ 인 다항식을 유도할 수 있습니다.

이렇게 다항식 형태로 문제가 변형된 뒤에는 다항식에 임의의 점을 넣어보고 같은 값을 가지면 두 다항식이 같다는 것을 보이면 됩니다. 따라서 QAP 변환을 통해 문제가 다항식 결과 값 비교로 간결해지게 됩니다.

실제 증명

단순한 QAP는 보안 성능이 높지 않습니다. 따라서 실제 zk-SNARK에서는 QAP를 타원곡선 위로 올립니다. 이러한 과정을 트러스티드 셋업이라고 합니다.

Trusted Setup

트러스티드 셋업은 zk-SNARK를 비대화형 영지식 증명 시스템으로 만드는 과정입니다. 검증자가 검증을 하기 위해 필요한 정보를 셋업 단계에서 생성해 공개하면 상호작용을 없앨 수 있습니다. 가장 많이 사용되는 방법은 전처리 단계를 통해 CRS(Common Reference String)를 만드는 것입니다. 이것은 증명자와 검증자 모두 접근 가능합니다.

트러스티드 셋업까지 마친다면 검증의 준비가 모두 끝났습니다. 실제 검증 과정을 알아보기 전에 필요한 것들을 알아보겠습니다.

Homomorphic Hidings

다음 조건을 만족하는 함수 $E(x)$ 를 동형 은닉, HH(Homomorphic Hidings)라고 하고 $x$ 의 hiding이라고 부릅니다.

대부분의 $x$ 에 대해 $E(x)$ 를 통해 $x$ 를 알 수 없다.
함수의 입력값이 다르면 출력값이 다르다.
$E(x)$ 와 $E(y)$ 를 알면 $x$ 와 $y$ 의 연산을 입력으로 갖는 HH를 만들 수 있다.

이를 이용한다면 증명자가 어떤 값을 알고 있다는 것을 값을 공개하지 않고 증명할 수 있습니다. 예를 들어 증명자가 $x + y = 0$ 인 두 값 $x$ , $y$ 를 알고 있다고 할 때, 증명자는 $E(x)$ , $E(y)$ 를 검증자에게 제공하는 것 만으로도 $x + y = 0$ 이라는 것을 증명할 수 있습니다.

보통의 정수 연산에서는 $E(x)$ 를 알면 $x$ 를 알아내기 쉽습니다. 따라서 HH는 유한군을 사용합니다. DLP 문제를 이용하면 유한군 $Z_p^*$ 에서 생성원 $g$ 를 이용해 $E(x) = g^x$ 가 HH인 것을 확인할 수 있습니다.

유한체 $\mathbb{F}_p$ 를 이용하면 다항식의 정보를 숨길 수 있습니다. 위에서 증명자가 증명하는 대상이 d차 다항식 $P(x) = a_0 + a_1x + a_2x^2 + \cdots + a_dx^d$ 라는 것을 알 수 있었습니다. 만약 다항식을 알고 있다면 특정 값을 대입하고 결과를 얻는 것이 쉽습니다. 증명자는 $P(x)$ 를 알고 있고 검증자는 유한체 $\mathbb{F}_p$ 안의 $s$ 를 알고 있다고 하겠습니다. 검증자가 $E(P(s))$ 를 알 수 있는 방법은 서로가 서로의 정보를 공유하는 것이지만 둘 다 서로의 정보를 몰라야 합니다. 따라서 HH를 이용해 $s$ 의 정보를 가리는 과정이 필요합니다.

검증자는 증명자에게 d차 다항식의 모든 $s$ 항에 대한 hiding인 $E(1), E(s), E(s^2), \dots, E(s^d)$ 을 만들어 보냅니다. 이를 통해 증명자는 $s$ 의 값을 유추할 수 없습니다.
증명자는 $E(P(s))$ 를 계산합니다. $s$ 값을 몰라도 $E(a_0 + a_1s + a_s^2 +\cdots + a_ds^d) = a_0E(1) + a_1E(s) + \cdots + a_dE(s^d)$ 를 만족하기 때문에 $E(P(s))$ 를 계산할 수 있습니다.

다만 여기서 검증자는 $P(x)$ 로 계산이 되었는지 알 수 없습니다. 그것 또한 검증할 수 있는데 그것을 위해서 Knowledge of Coefficient test라는 개념이 사용됩니다.

Pairing of Elliptic Curve

위에서 QAP를 타원곡선 위에 올리는 트러스티드 셋업을 진행했습니다. 트러스티드 셋업 후에는 증명자가 수식에 값을 넣고 QAP로 변환 후에 동형 은닉을 통해 검증자에게 수식을 공개하지 않고 다항식의 나눗셈 연산으로 검증 과정을 진행할 수 있습니다. 이를 위해 타원곡선 군에서 곱셈과 덧셈을 모두 지원하는 HH가 필요합니다. 타원곡선의 페어링은 겹선형사상이라고도 하며 타원곡선위에서 동형암호화를 하는 방법을 제공합니다. 먼저 타원곡선의 페어링을 위해 특정 그룹들을 정의합니다.

$G_1$
생성원이 $g$ 고 원소의 개수가 $r$ 개이며 덧셈이 가능한 타원곡선 군입니다.
$C$ ( $\mathbb{F}_p^k$ )
$r$ 이 $p^k - 1$ 의 약수가 되도록 하는 가장 작은 정수 $k$ 가 6 이상인 경우 타원곡선 군이 ECDLP 문제를 풀기 어렵습니다. 또한 $\mathbb{F}_p$ 와 함께 $\mathbb{F}_{p^k}$ 또한 타원곡선의 좌표가 되며 덧셈 규칙을 만족합니다.
$G_2$
$G_1$ 의 부분군으로 원소의 개수가 $r$ 개이고 생성원이 $h$ 이고 덧셈이 가능한 타원곡선 군입니다.
$G_t$
$\mathbb{F}_{p^k}$ 는 원소의 개수가 $r$ 개인 $G_t$ 를 부분군으로 가집니다. $G_t$ 는 원소 개수가 $r$ 개이고 생성원으로 $g'$ 을 가지고 곱셉연산을 지원하는 군입니다.

여기서 $G_1$ 과 $G_2$ 의 원소쌍을 $G_t$ 로 가져가는 매핑이 존재합니다. $G_1$ 과 $G_2$ 의 원소를 연산하면 $G_t$ 의 원소가 되는 특정 함수를 Tate reduced pairing이라고 부릅니다. 따라서 앞서 정의한 군과 Tate 함수를 이용해 곱셈과 덧셈 모두를 지원하는 HH를 정의할 수 있습니다.

zkRollup

블록체인에서 네트워크에 참여하는 모든 노드는 모든 트랜잭션을 독립적으로 처리하며 한번 등록된 데이터는 수정 불가능합니다. 따라서 각각의 노드가 저장해야할 용량이 커지고 처리 속도도 느려지게 되었으며 수수료(가스) 또한 많이 들게 되었습니다. 롤업(rollup)이란 블록체인에 써야하는 내용을 압축하는 것을 말합니다. 이를 통해 트랜잭션의 크기가 작아지게 됩니다.

롤업은 보통 블록체인 외부에서 트랜잭션을 실행하고 데이터 또는 증거를 블록체인에 기록합니다. 이 때 트랜잭션 데이터가 유효한지에 대한 검증이 필요한데, 영지식 롤업은 이때 영지식 증명을 사용합니다. 유효성 검증을 위해 블록체인 외부로 이동해 트랜잭션을 검증하고 결과만을 트랜잭션에 기록합니다.

암호학의 기본 정의에서 시작해 현대 암호학의 다양한 성취와 가장 최근에 만들어진 영지식 증명까지 살펴보았습니다. 다른 주제로도 블로그 글은 계속 쓸 예정이며 내용에 관한 질문, 제안, 잘못된 내용 정정 요청 모두 댓글 또는 soowon1106@gmail.com으로 메일 부탁드리겠습니다. 감사합니다.

Soowon Jeong

이전 포스트