알고리즘

• 알고리즘 문제 해결 절차를 배운다.
• 시간 복잡도를 통해 효율적인 알고리즘에 대해 알아본다.
• 완전 탐색의 개념에 대해 배워본다.

1. 문제 해결의 절차

1. 문제를 정확히 이해한다.
2. 문제를 해결하는 알고리즘을 개발한다.(어려움)
3. 알고리즘이 문제를 해결한다는 것을 증명한다.
4. 알고리즘이 제한시간내에 동작한다는 것을 보인다.(효과성이 있어야 한다.)
5. 알고리즘을 코드로 작성한다.

2. 시간 복잡도

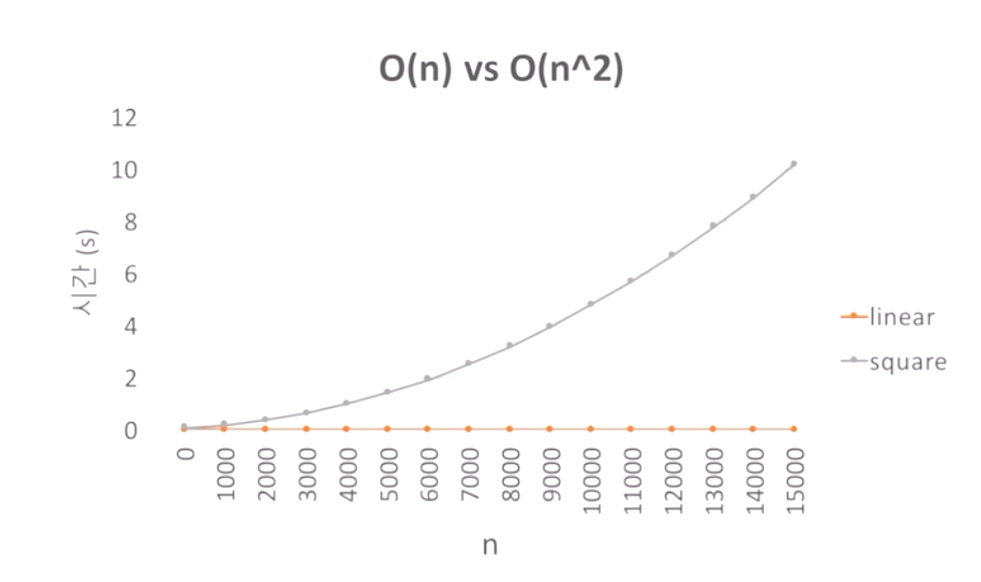
• 정확히 몇 번 수행하는가가 아닌 대략적으로 몇 번 수행하는가를 물어봄
  따라서 n^2+2n+3에서 n이 1000일때 n^2는 백만이지만 2n은 2000에 불과하다 이는 무시해도 될 정도의 수 이며 대략적으로 n^2이라고 시간 복잡도를 유추할 수 있다.
• Big-O표기 : 최악의 경우에 수행하는 명령 수
  어떠한 배열에서 특정 숫자를 찾는다고 할 때 운이 좋다면 앞에서 찾을 수 있지만 운이 안 좋으면 제일 뒤에서 찾을 수도 있다. 이에 따라 항상 최악의 시간복잡도를 표기하는데 이를 Big-O표기라고 한다.
  

3. 완전 탐색(brute-Force)

• 가능한 모든 경우를 시도해 보는 것, 가능한 모든 경우가 무엇인가를 파악하는 것.
• 가능한 모든 경우를 전부 고려해도 괜찮을 경우에 즉, 모든 경우를 고려하여도 제한시간안에 문제를 해결할 수 있다면 사용
  단순히 모든 경우를 고려함으로써 문제를 해결한다.
• 어떤 문제가 주어지건 무조건 완전 탐색법으로 먼저 시도해야한다.
• 상식적인 문제 해결의 흐름
  

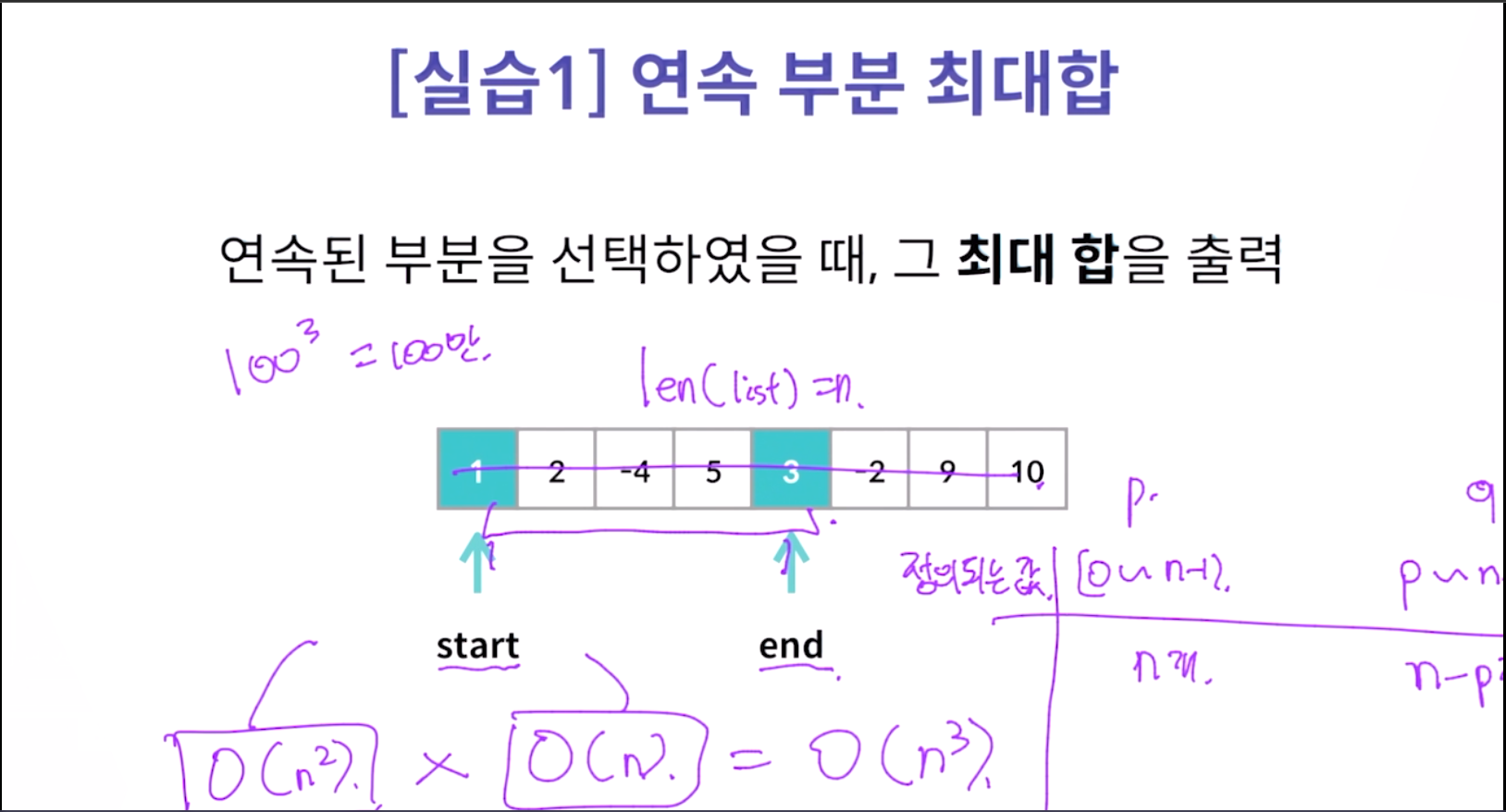
[실습]for문을 돌리면 개오래 걸림 그래서 재귀함수로 이 문제를 해결할 것임.
재귀호출로 풀기위한 조건 3단계

1. 함수의 정의를 명확히 => 전체 경우 : 1을 선택하는 경우와 그렇지 않은 경우
2. 기저조건에서 잘 돌아가야함 => 사진 1 을 보면 뭔가 계속 줄어들다가 마지막 남은 1개(이 경우에서는 3)가 있다. 이 경우를 기저조건(더이상 함수가 안으로 들어갈 수 없는 가장 기본이 되는 조건)이라 부를 것이다.
   즉 이 경우에서는 getPowerSet(n,k) n==k일때
3. 기저조건이 아닐 때 잘 동작하게해야함.

4. Complexity

• 복잡도 이론 : 각 문제마다 불이의 시간복잡도가 다르기 때문에 내 풀이가 얼마나 좋은 풀이인가를 확인하는 것이다.
  예를 들어 정렬 문제같은 경우의 시간복잡도는 O(nlogn)이다.
• 문제자체에도 복잡도가 존재한다. 다항시간 안에 풀 수 있는 문제를 P class 문제라고 한다. 또한 NP-Complete class는 답을 검증하는데 다항시간이 걸린다는 의미. 특히 NP class 문제들 중에서도 푸는 시간이 매우 오래 걸리는 문제들을 의미함
• 다항시간이란 O(n^2),O(n^2) 다항이 아닌시간은 O(2^n),O(n!) 따라서 어떤 문제가 주어졌을 때 다항시간 이내에 풀 수 있다는 것은 매우 중요한 문제이다.

알고리즘 과정에서 다루는 문제들

• 대부분 P문제들만을 다룬다.
• 알고리즘에서는 고려해야 하는 경우를 줄이는 방법을 배운다.
• 대표적인 NP-Complete 문제는 알면 좋다.

5. 요약

1. 문제 해결 절차(1~6단계)를 잘 따라야 한다. [그중 3, 4번째가 가장 경우]
2. 모든 경우를 고려해도 괜찮은 경우에는 모든 경우(완전탐색)를 고려하여 해결한다.