1. 우선순위 큐
- 출력 연산 시 가장 우선순위가 높은 원소를 출력한다.
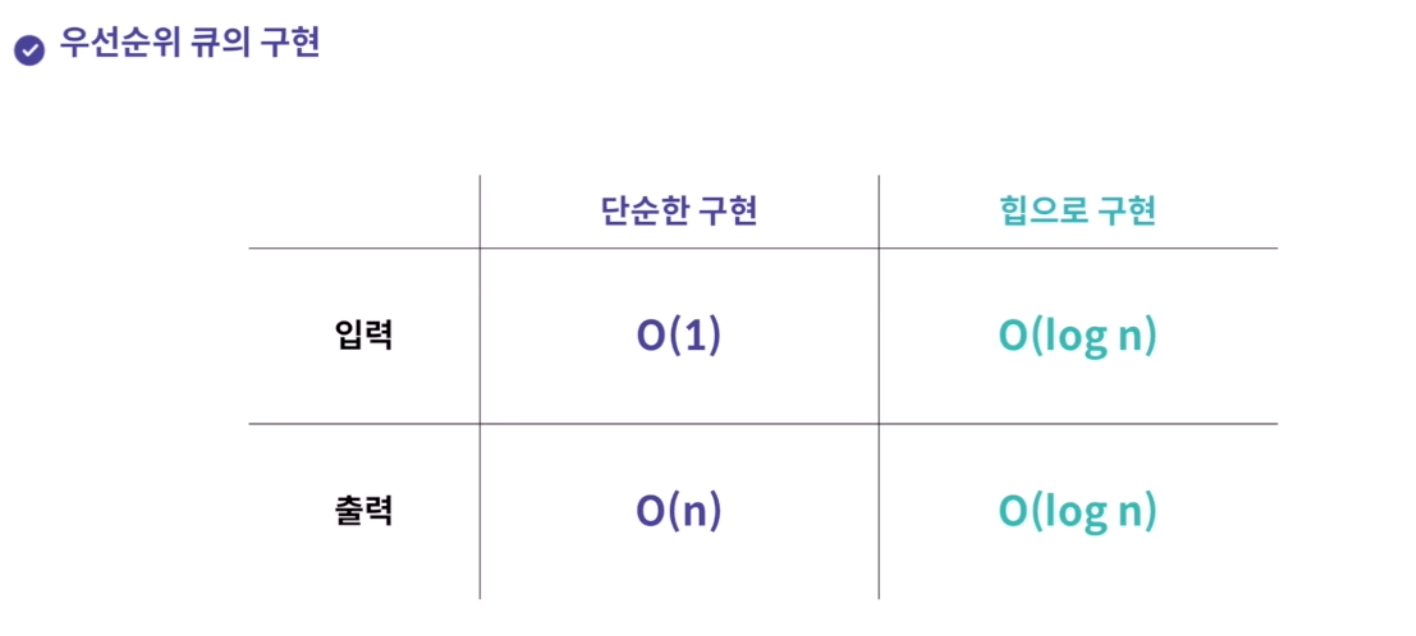
- 이때 배열로 구현한다면 시간복잡도에 있어 매우 불리하다.
그래서 고안된 방법이 바로 완전이진트리(힙)이다. 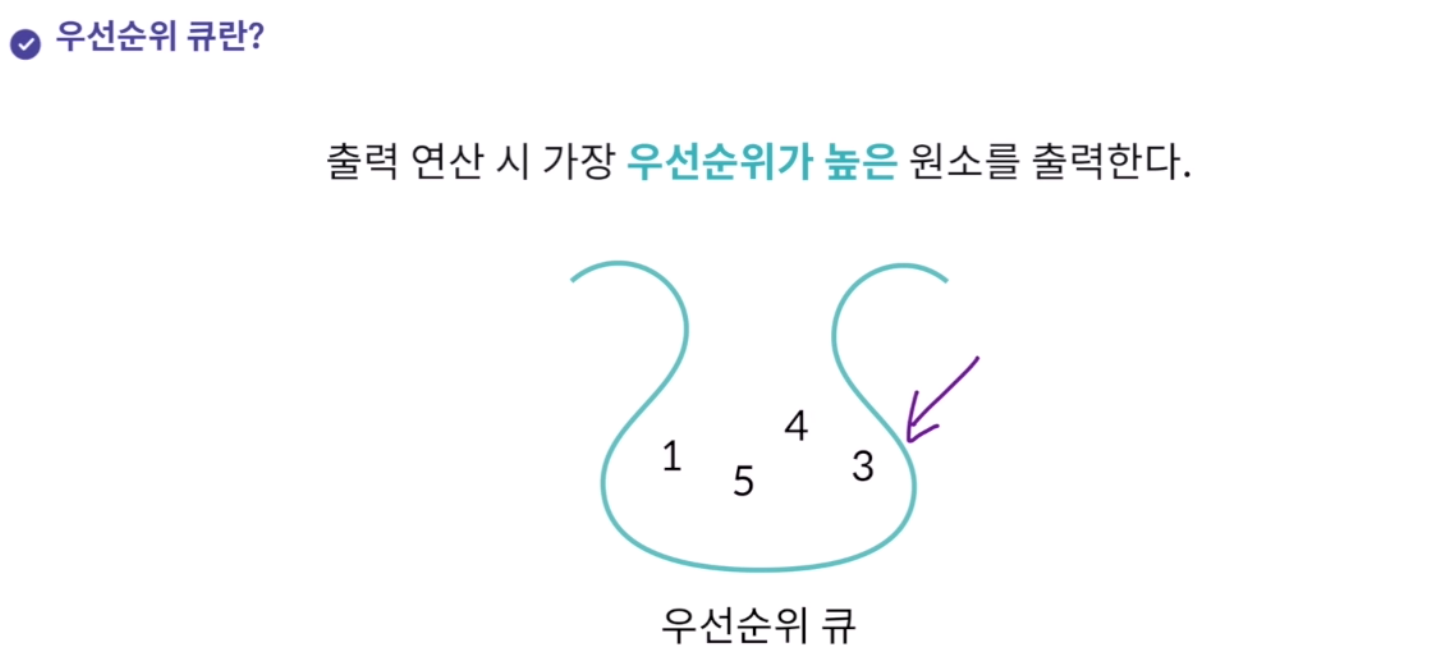
2. 힙
- Max Heap : 부모노드는 항상 자식 노드보다 큰 값을 갖고있다.
- Min Heap : 부모노드는 항상 자식 노드보다 작은 값을 갖고있다.
- Heap은 python의 heapq module로 Min Heap을 사용할 수 있다.
따라서 이를 이용하여 Max Heap을 사용하려면 값을 저장할 때 -1만 곱해주면 된다. 단, 이 방법은 힙이 저장하는 값이 number일 때만 유효하다.
1) 힙 : 자료입력
- 완전 이진트리를 사용하므로 항상 오른쪽 가장 밑에 넣어줘야한다. 하지만 완전 이진트리의 특성을 유지하기 위해 부모노드보다 더 작다면 수를 바꿔줘야한다.
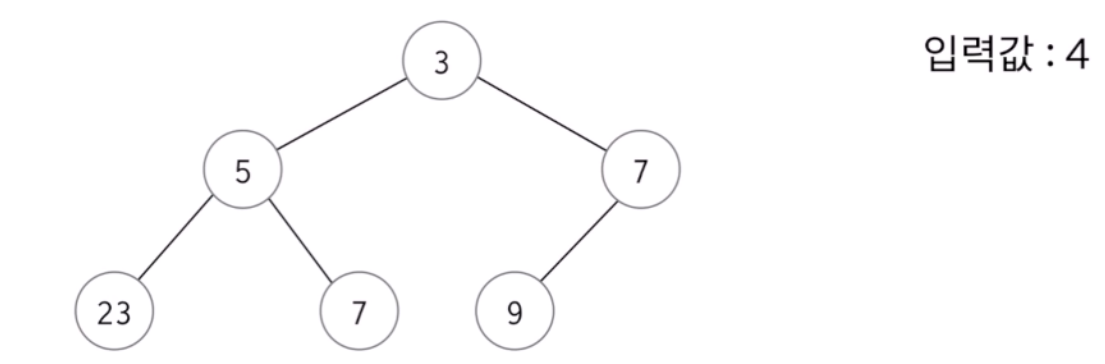
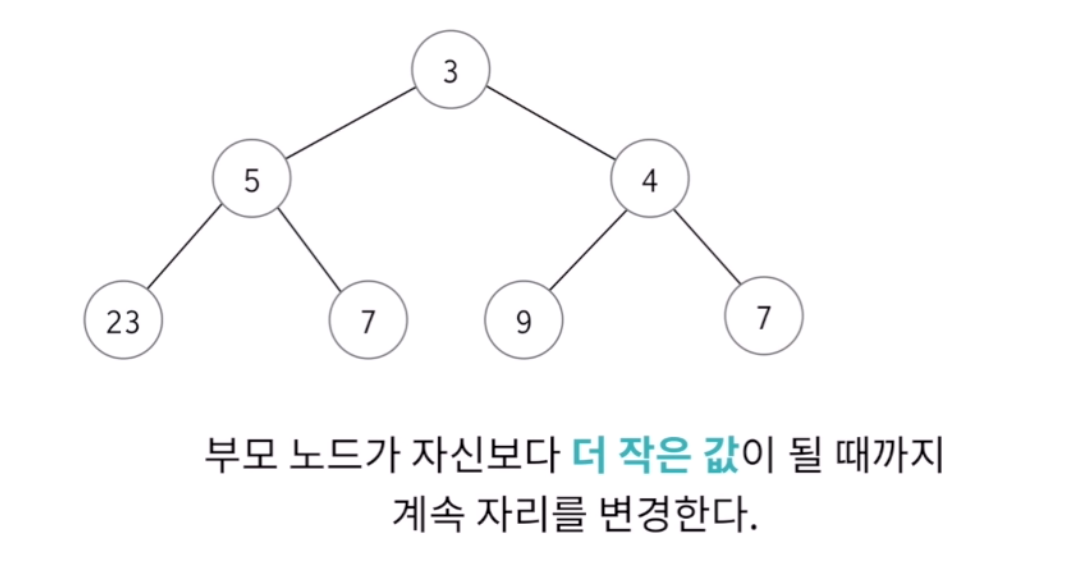
- 즉!! 부모노드와의 대소관계와 완전이진트리의 특성을 유지한 채 자료를 입력하면 된다.
이때 발생하는 시간복잡도는 전체 노드에서 가장 작은 수가 입력되는 경우이고 루트 노드까지 거슬러 올라게 된다. 이때 발생하는 연산횟수는 트리의 높이와 비례하므로 logn의 시간 복잡도를 갖게 된다.
2) 힙 : 자료출력
- 항상 루트 노드가 출력되며 가장 최하단에 있는 자료가 루트 노드위치로 가며 이진트리 특성을 유지하고자 다시 한번 조건을 맞춰가며 자리를 확정한다.
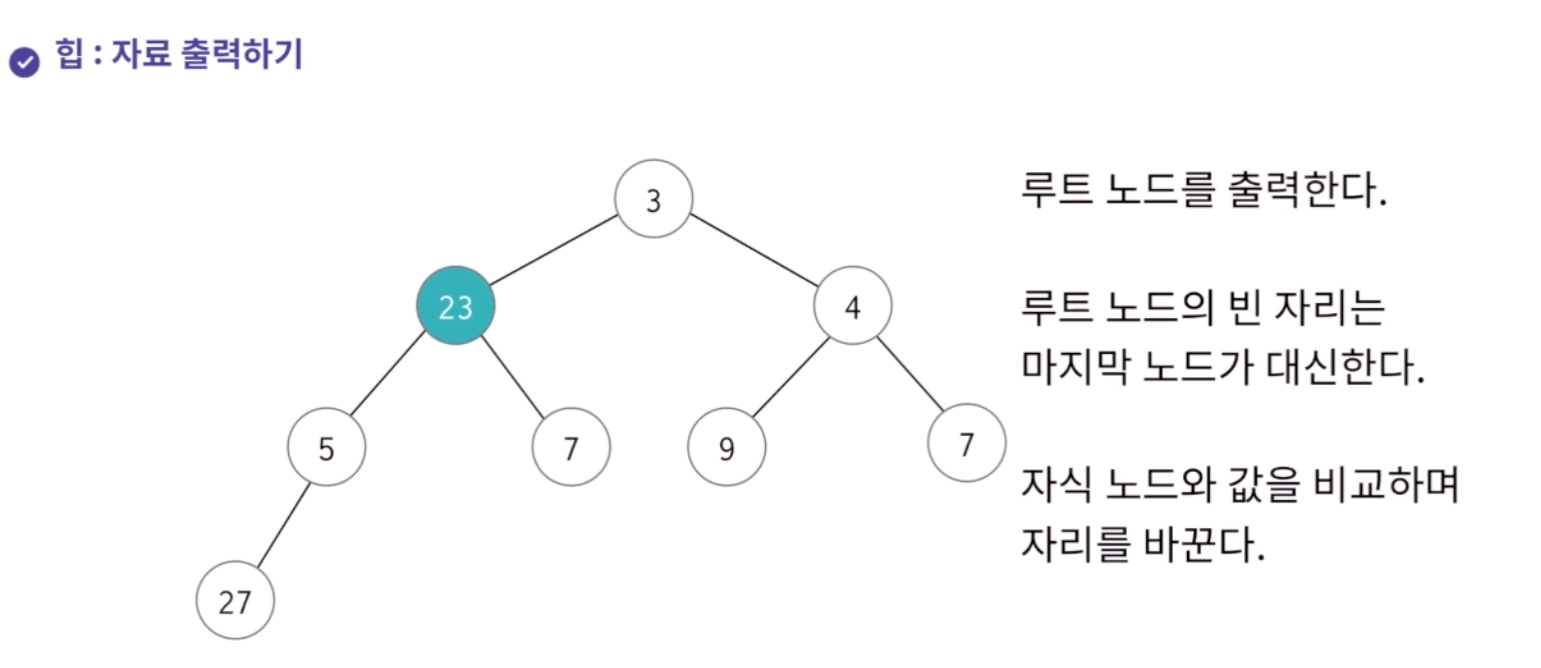
- 이때 발생하는 시간복잡도는 맨 마지막 원소가 가장 큰 값을 가진 경우이다. 이대 자리를 바구는 연산의 횟수는 트리의 높이만큼 이루어지므로 logn의 시간 복잡도를 갖게된다.
3) 결론 :
3. 힙을 이용한 문제풀이
- 힙을 이용하여 정렬을 구현한다면 모든 자료를 힙에 입력하고 모든 정수를 출력하면 된다. 왜냐? 어차피 힙을 출력할 때는 저장하고 있는 자료중 최솟값을 반환하니까
- 이때의 시간복잡도

* 점토놀이
- 점토를 합칠때 마다 합쳐진 점토만큼의 힘이 든다면 가장 작은 수의 점토부터 합쳐야 개이득이다.
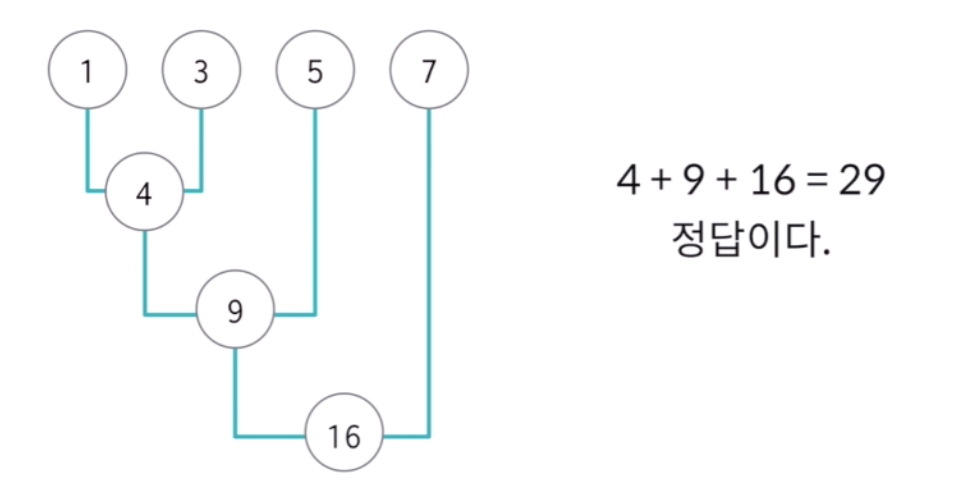
- 하지만 조건에 부합하지 않을 수도 있다.
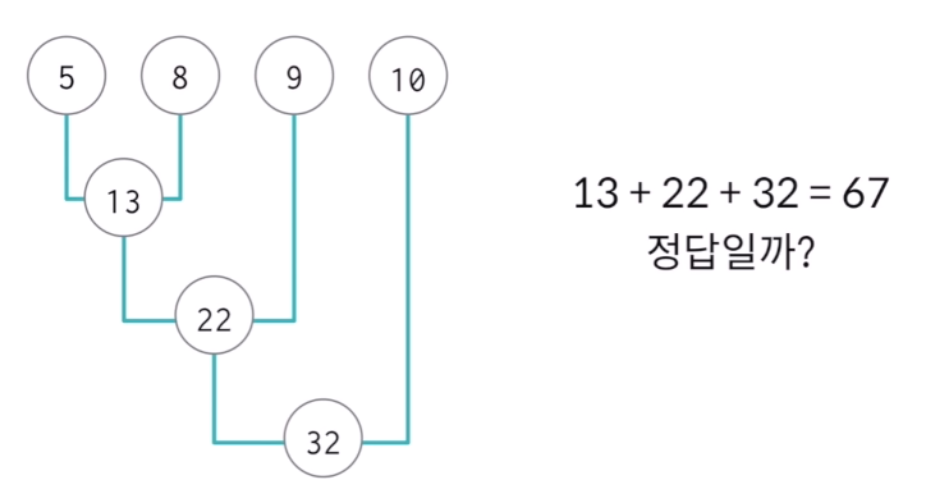
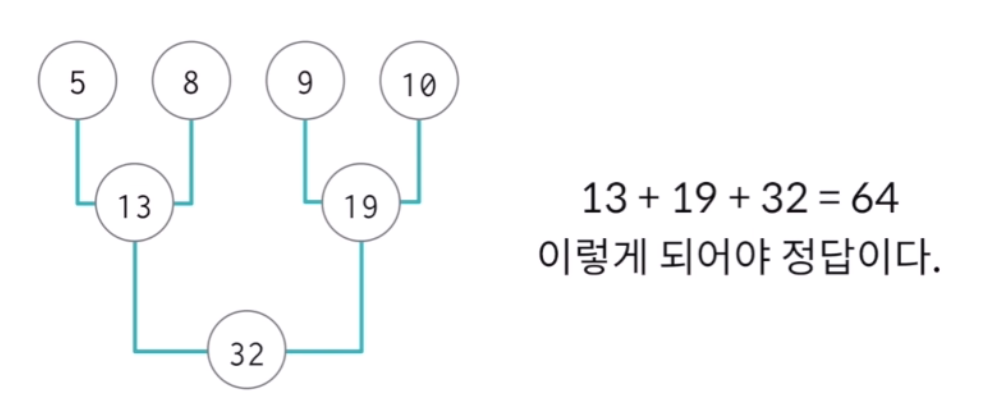
- 따라서
1.점토들을 모두 힙에 저장한다.
2.가장 가벼운 두 점토를 꺼내서 합치고, 다시 힙에 저장한다.
3.점토가 하나가 될 때까지 1번부터 반복한다.
* 중간값 찾기
- n개의 요소를 갖는 배열이 주어진다면 n번만큼의 중간값을 출력하는 함수를 만들어야 한다. 이를 배열로 정리하게된다면 매번 정렬해야 하기 때문에 시간 복잡도는 n^2*logn이 된다. ㄸ라서 제한시간내에 문제를 해결할 수 없다.
- 힙에서는 항상 최소또는 최댓값을 logn의 시간에 찾아낼 수 있는 것 처럼 중간값을 빠르게 찾아낼 방법이 필요하다.
- 방법은 다음 포스트에서...