분할정복법

1. 재귀호출을 이용한 문제 해결

1) 재귀함수의 올바른 디자인 및 해석

재귀함수를 디자인하기위한 3가지 단계
1) 함수의 정의를 명확히 한다.
2) 기저 조건에서 함수가 제대로 동작하게 작성한다.
3) 함수가 제대로 동작한다고 가정하고 함수를 완성한다.

2. 분할정복법

• 사실 퀵정렬도 분할정복법 중 하나이다.
• 분할정복법은 크게 3가지로 나눌 수 있다.

1. 문제를 소문제로 분할
2. 각각의 소문제를 해결
3. 소문제의 해결 결과를 이용해 전체 문제를 해결

• 가장 큰 문제는 어떤 분할정복으로 풀어야하는지(문제를 소문제를 분할하는지)가 가장 어려움
• 분할 정복법으로 해결할 수 있는 대표적인 예제
• 수학적 문제 해결 능력이 가장 중요
• 키보드 대신 노트와 펜을 들고 생각

(1) 합병정렬

• 2개의 배열을 2로 나눈다음 큌정렬을 진행 후 다시 합칠 때 2개의 요소를 하나하나 비교해가며 합친다.
  즉, 합병정렬의 시간복잡도는 n개를 정렬하는데 드는 시간 =T(n)이다.
  T(n)은 T(n/2) + T(n/2) + O(n)
  log n * O(n) = O(n logn)

(2) 연속부분 최대합

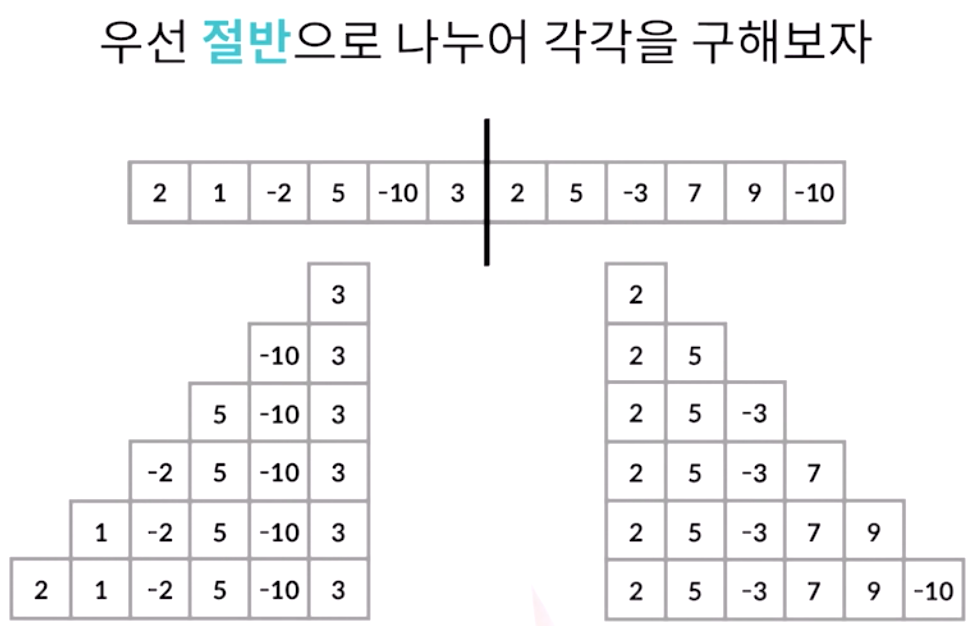
3. 요약

• 분할정복접으로 해결할 수 있는 대표 예제
  1.합병정렬
  2.퀵정렬
  3.거듭제곱 구하기
  4.연속 부분 최대합
  5.가장 가까운 두 점 찾기

6. 히스토그램
   위의 예제들을 연습하며 매우 어려운 분할정복법을 공부하자