Strongly Connected Component
📝 정의
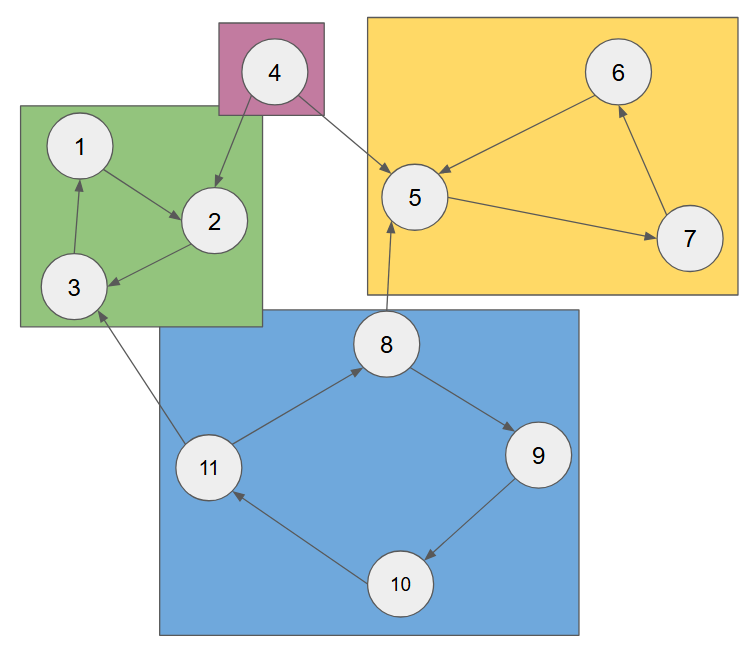
그래프 안에서 강하게 결합된 정접 집합을 뜻한다. 서로 긴밀하게 연결되어 있다고 하여 강한 결합 요소라고 말한다.
🛠 특징
SCC 라고도 불린다.
SCC 는 같은 SCC 에 속하는 두 정점은 서로 도달이 가능하다는 특징을 갖고 있다.
당연하게도 서로에게 도달하려면 무조건 사이클이 발생해야만, SCC 라는 것을 알 수 있다.
이는, 방향 그래프일 때만 의미가 있다. 무향 그래프라면 그 그래프 전체는 무조건 SCC이기 때문이다.
(왜냐면 무향으로 서로 양방향이면 서로 2개의 노드만 해도 벌써 강한 결합이기 때문에 의미 X)
with 위상정렬
이 SCC 로 만은 크게 문제를 해결하지 않고, 이 SCC 와 위상정렬을 함께 수행하여 크게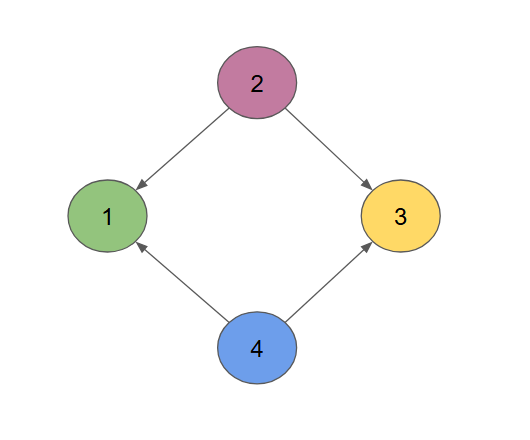 
위 사진과 같은 구조로 나눈 후 각 SCC 를 위상 정렬 하여 문제를 해결한다.
⏰ 시간 복잡도
타잔 알고리즘의 시간 복잡도는 위상 정렬의 시간 복잡도와 동일한 O(V+E) 이다.
⚙ 동작
이제 이러한 특징적인 그래프에서 SCC 를 추출하는 알고리즘은 대표적으로 코사라주 알고리즘(Kosaraju's Algorithm)과 타잔 알고리즘(Tarjan's Algorithm)이 존재한다.
-
구현이 더 쉬운거
코사라주 알고리즘(Kosaraju's Algorithm) > 타잔 알고리즘(Tarjan's Algorithm) -
적용이 더 쉬운거
코사라주 알고리즘(Kosaraju's Algorithm) < 타잔 알고리즘(Tarjan's Algorithm)
따라서 우리는 타잔 알고리즘으로 이 SCC 를 찾아볼 것이다.
타잔 알고리즘
모든 정점에 대해 DFS를 수행하여 SCC를 찾는 알고리즘이다.
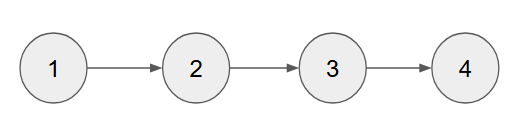우선 위 그래프는 SCC가 아니다. 왜냐하면 SCC는 부모로 돌아올 수 있어야 하기 때문이다.
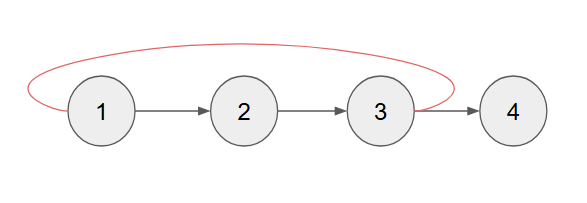이제 위 그래프는 SCC이다. 왜냐하면 1~3 중 어느 정점을 골라도 서로에게 도달할 수 있는 경로가 생기기 때문이다.
따라서 위 그래프는 1~3 는 SCC이다.
그래서 이를 검증하기 위해 부모에서 자식으로 나아가는 알고리즘으로 DFS 알고리즘이 사용되는 것이다.
-
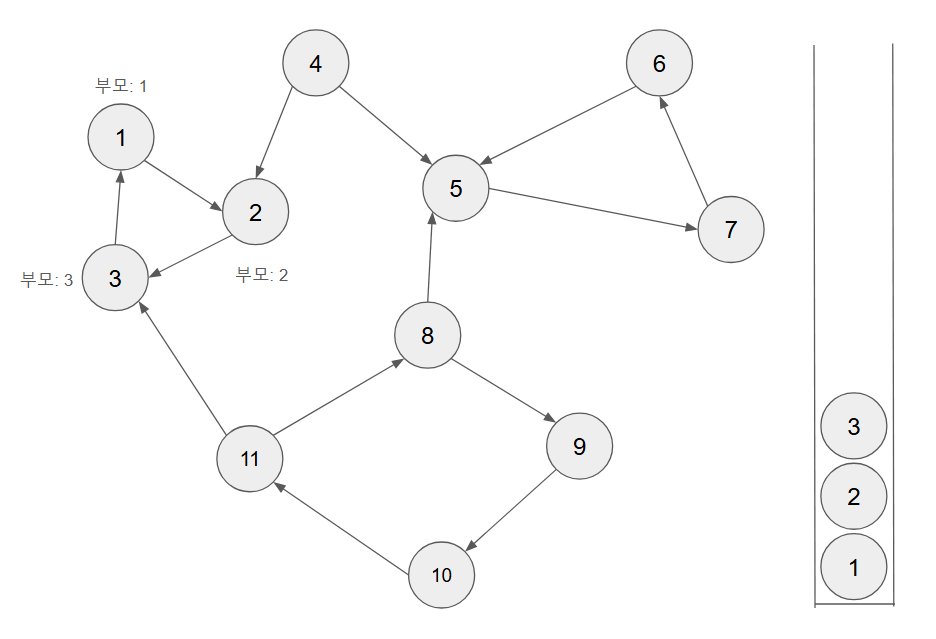
정점 1에 대하여 DFS 를 수행한다. DFS는 또 다른 정점을 기준으로 DFS를 수행한다. 이때, 부모는 자기 자신으로 설정한다. 그리고 본인의 자식으로 나아간다.
-
이제 DFS를 수행하며 자식으로 나아갈 때 DFS가 안 끝났는데, stack 에 쌓인 값에 자식의 값이 들어있다면 이는 사이클이 생기고 이는 SCC가 형성되었다는 것을 알 수 있다.
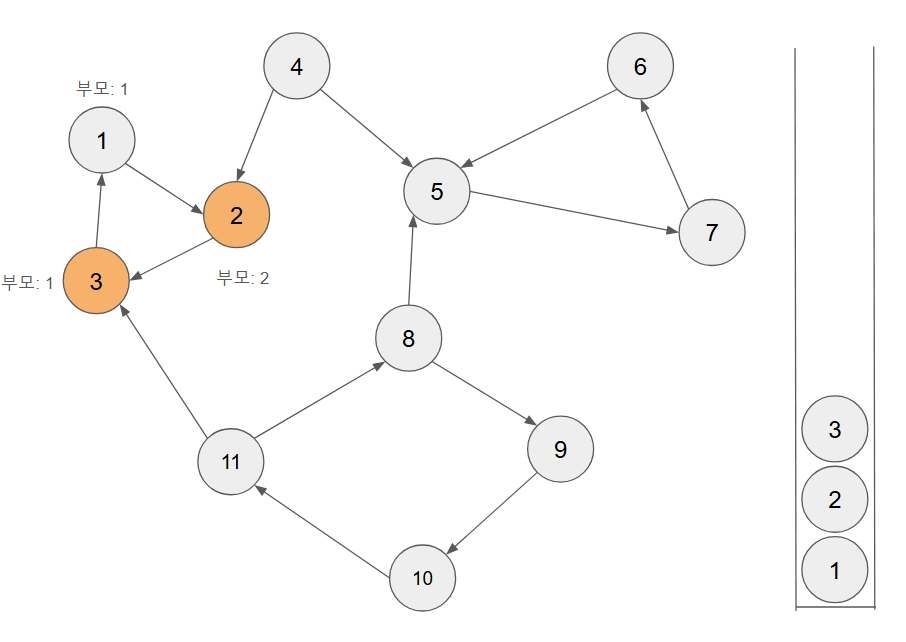
- 그리고 3번을 내보내고 2번으로 돌아가서 아직 stack 에 1번이 담겨있는 상태(1번에 대한 DFS가 끝나지 않은 상태)이기 때문에 부모가 1인 것을 알 수 있고
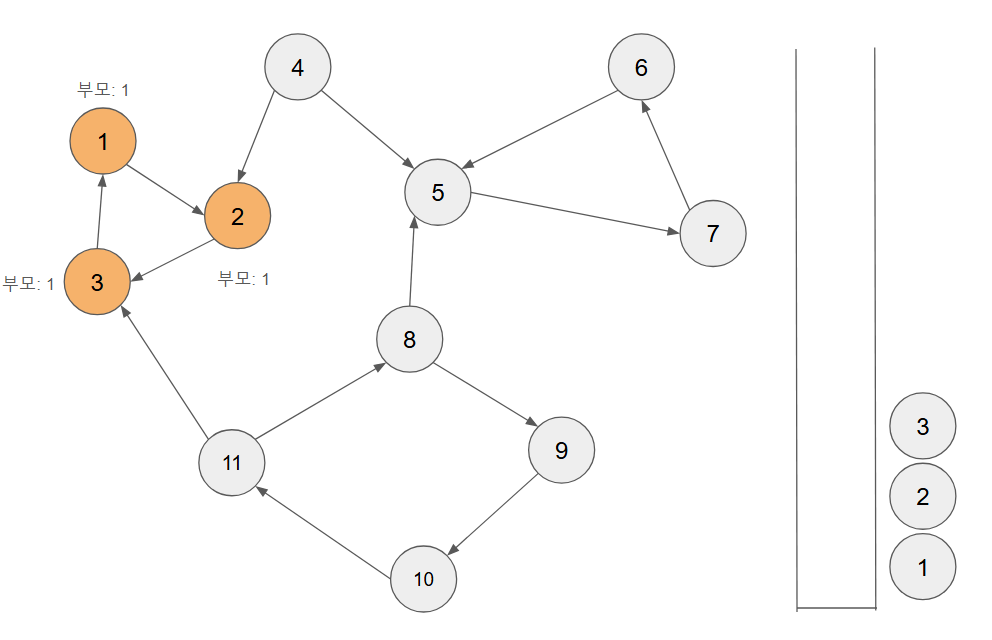
- 이제 1번으로 돌아가서 인접한 노드가 없기 때문에 DFS 가 끝난 상태인데 부모값과 자기 자신이 같은 상태이므로 본인이 DFS에서 부모값에 해당하는 부분인 것을 알 수 있다.
이제 이를 반복하면
-
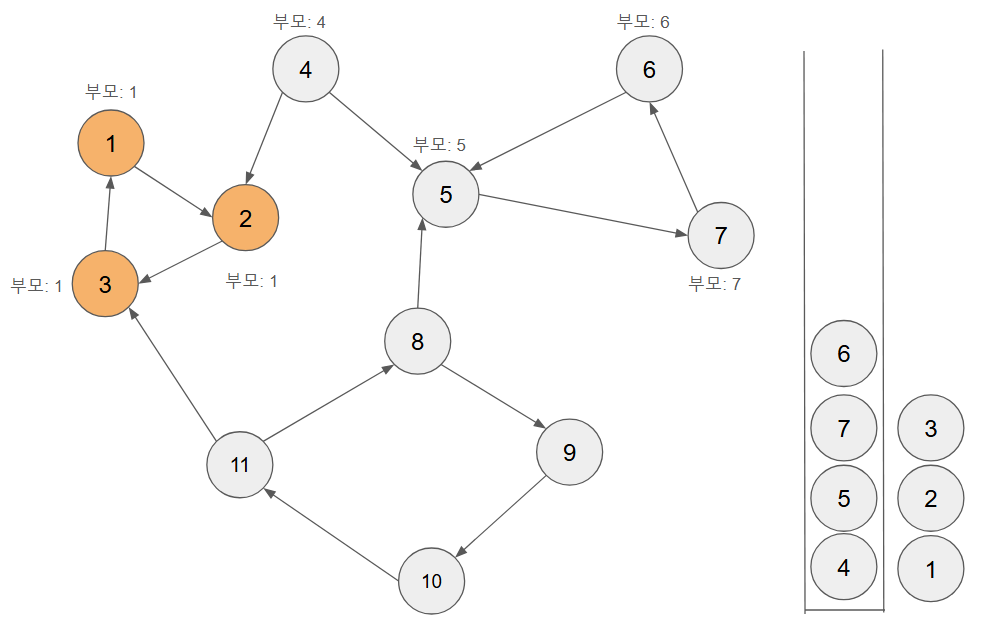
4에 대하여 시작하여 5,7,6 을 거쳐 DFS 수행
-
6을 DFS 수행할 때 stack 에 자식 노드인 5가 들어있는 것을 발견 부모를 5로 수정
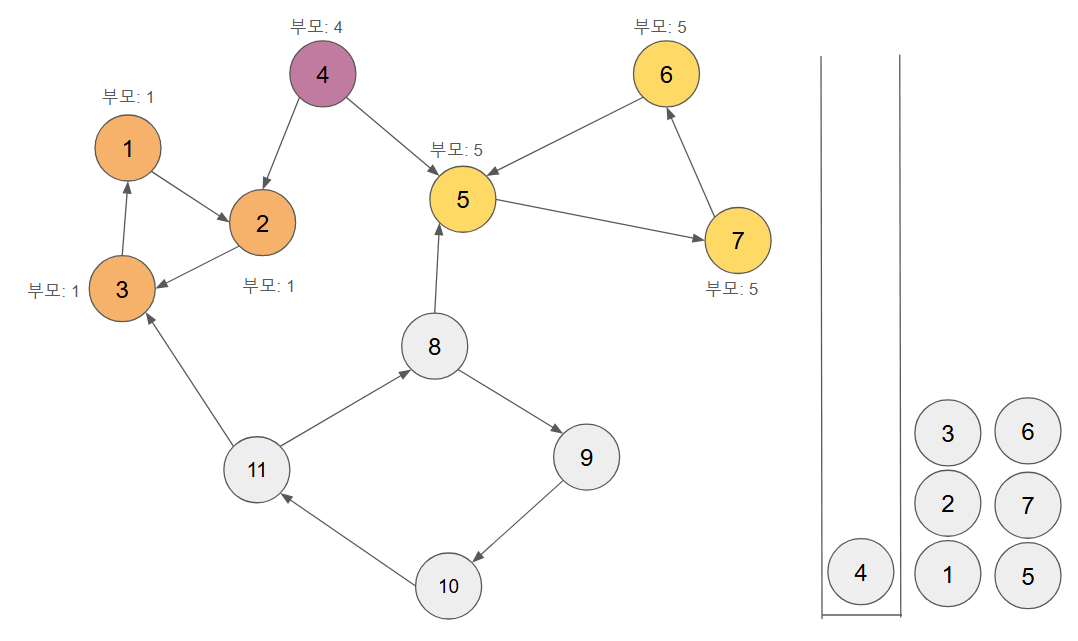
- 이제 5로 돌아가서 인접 노드가 없기 때문에 5,7,6 을 SCC 로 설정,
4로 돌아가서 역시 인접 노드가 없기 때문에 4 본인을 SCC 로 설정.
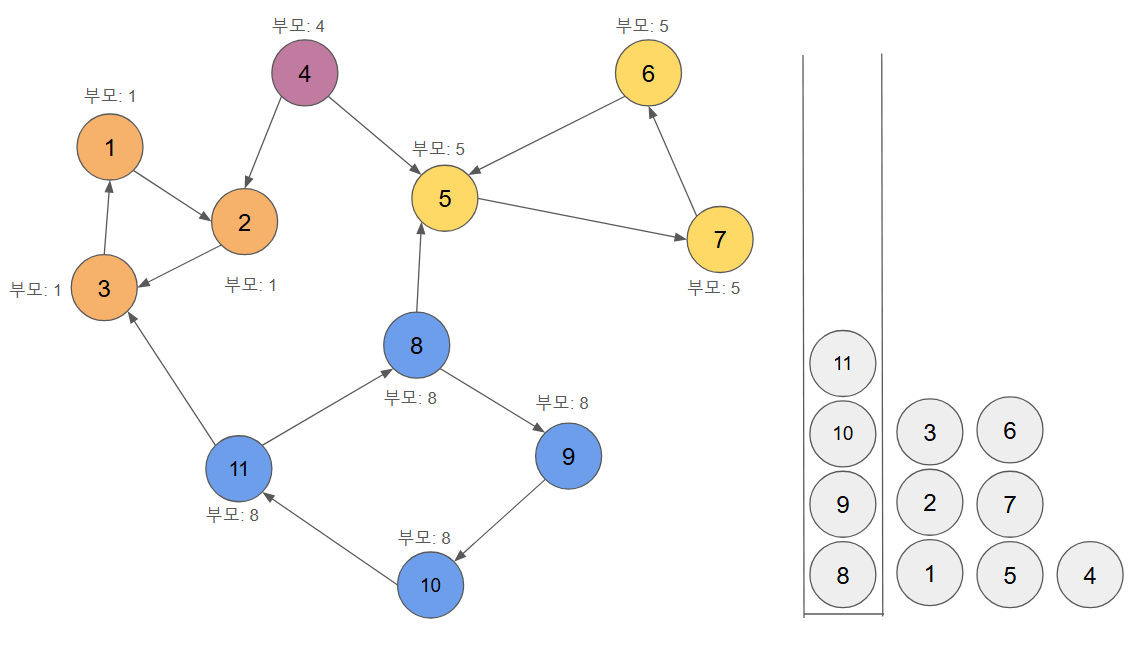
- 이를 반복하여 최종 결과값을 확인한다.
💻 코드
import java.util.*;
public class SCC {
private int nodeCount; // 총 노드 수
private List<List<Integer>> graph; // 그래프 인접 리스트 표현
private int[] ids; // 각 노드의 고유 번호
private int[] low; // 각 노드의 최소 고유 번호
private boolean[] onStack; // 스택에 포함 여부
private Stack<Integer> stack;
private int id; // 현재 탐색 중인 고유 번호
private List<List<Integer>> sccs; // SCC 결과 저장
public SCC(int nodeCount) {
this.nodeCount = nodeCount;
this.graph = new ArrayList<>();
for (int i = 0; i < nodeCount; i++) {
graph.add(new ArrayList<>());
}
this.ids = new int[nodeCount];
Arrays.fill(ids, -1); // 아직 방문하지 않은 노드는 -1로 초기화
this.low = new int[nodeCount];
this.onStack = new boolean[nodeCount];
this.stack = new Stack<>();
this.id = 0;
this.sccs = new ArrayList<>();
}
public void addEdge(int from, int to) {
graph.get(from).add(to);
}
public List<List<Integer>> findSCCs() {
for (int i = 0; i < nodeCount; i++) {
if (ids[i] == -1) {
dfs(i);
}
}
return sccs;
}
private void dfs(int at) {
stack.push(at);
onStack[at] = true;
ids[at] = low[at] = id++;
for (int to : graph.get(at)) {
if (ids[to] == -1) { // 방문하지 않은 노드
dfs(to);
low[at] = Math.min(low[at], low[to]);
} else if (onStack[to]) { // 스택에 있는 노드라면
low[at] = Math.min(low[at], ids[to]);
}
}
// SCC 추출
if (ids[at] == low[at]) {
List<Integer> scc = new ArrayList<>();
while (true) {
int node = stack.pop();
onStack[node] = false;
scc.add(node);
if (node == at) break;
}
sccs.add(scc);
}
}
public static void main(String[] args) {
SCC tarjan = new SCC(12);
// 그래프 간선 추가
tarjan.addEdge(1, 2);
tarjan.addEdge(2, 3);
tarjan.addEdge(3, 1);
tarjan.addEdge(4, 2);
tarjan.addEdge(4, 5);
tarjan.addEdge(5, 7);
tarjan.addEdge(7, 6);
tarjan.addEdge(6, 5);
tarjan.addEdge(8, 5);
tarjan.addEdge(8, 9);
tarjan.addEdge(9, 10);
tarjan.addEdge(10, 11);
tarjan.addEdge(11, 8);
tarjan.addEdge(11, 3);
// 강결합 컴포넌트 찾기
List<List<Integer>> sccs = tarjan.findSCCs();
// 결과 출력
System.out.println("Strongly Connected Components:");
for (List<Integer> scc : sccs) {
System.out.println(scc);
}
}
}