🔮 백준 26091. 현대모비스 소프트웨어 아카데미

문제

현대모비스는 글로벌 자동차 부품 기업으로 자율주행, 커넥티비티, 전동화 분야에 역량을 집중해 스마트 모빌리티 시대를 선도하고 있는 기업입니다.

현대모비스는 소프트웨어 생태계 조성을 위해 소프트웨어 아카데미를 운영하고 있으며, 내부적으로는 연구원들의 소프트웨어 직무교육 이수를 통해 우수인재를 육성하고, 대외적으로는 채용 연계형 프로그램을 운영하여 취업 준비생들에게 소프트웨어 전문 교육을 무상으로 제공하고, 더 나아가 우수 이수자들을 채용하고 있습니다.

현대모비스에서 소프트웨어 아카데미 견학생을 모집한다고 한다. 이번 견학 활동은 모두 팀 단위로 진행되며 아래 두 조건을 모두 만족하는 팀만 소프트웨어 아카데미를 견학할 수 있다.

• 팀원이 두 명이다.
• 팀의 능력치가 M 이상이다. 팀의 능력치는 모든 팀원의 능력치를 합한 값이다.

Sogang ICPC Team 학회원 N명이 견학을 희망한다. 학회장 동건이는 N명으로 최대한 많은 팀을 만들어 견학을 보내고 싶다. 동건이가 최대 몇 팀이나 견학 보낼 수 있을지 구해보자.

입력

첫째 줄에 견학을 희망하는 학회원의 수 N과 견학하는 팀의 최소 능력치를 나타내는 정수 M이 공백으로 구분되어 주어진다. (1 <= N <= 100000, 1 <= M <= 10^9)

둘째 줄에 학회원 N명의 능력치를 나타내는 N개의 정수 a_1,a_2, ..., a_N이 공백으로 구분되어 주어진다. (1 <= a_i <= 10^9)

출력

첫째 줄에 동건이가 견학 보낼 수 있는 최대 팀 수를 출력한다.

예제 입력 1

6 10
3 5 7 3 5 6

예제 출력 1

2

예제 입력 2

1 10
100

예제 출력 2

0

알고리즘 분류

• 그리디 알고리즘
• 정렬
• 두 포인터

풀이

• 견학을 원하는 인원 수 N
• 팀 최소 능력치 M
• 리스트 정렬하기
• 투포인터를 활용하여 합하여 M보다 큰 값들을 추출

코드

N, M = map(int, input().split())
arr = list(map(int, input().split()))
arr.sort()
left, right = 0, N-1
count = 0

for i in range(N//2):
    if left >= right:
        break
    elif arr[left] + arr[right] >= M:
        count += 1
        left += 1
        right -= 1
    else:
        left += 1
print(count)

---

🔮 백준 16507. 어두운 건 무서워

문제

호근이는 겁이 많아 어두운 것을 싫어한다. 호근이에게 어떤 사진을 보여주려는데 사진의 밝기가 평균 이상이 되지 않으면 일절 보려 하지 않는다. 호근이가 이 사진에서 일부분이라도 볼 수 있는 부분을 찾아주자.

위 그림은 호근이에게 보여줄 5×6 크기의 사진이며, 각 픽셀은 밝기를 나타낸다. 호근이가 사진의 일부분이라도 볼 수 있는지 알아보기 위해서는 두 점 (r1, c1)과 (r2, c2)를 꼭짓점으로 하는 직사각형의 밝기 평균을 구해야 한다. 예를 들어, 위 그림에서는 (2, 2)와 (4, 5)를 꼭짓점으로 하는 직사각형을 말한다.

호근이에게 보여줄 R×C 크기의 사진이 주어질 때, 사진의 일부분에 해당하는 밝기 평균을 구하여라.

입력

첫 번째 줄에는 사진의 크기를 의미하는 정수 R, C (1 ≤ R, C ≤ 1,000)와 사진 일부분의 밝기 평균을 알아볼 개수를 의미하는 정수 Q (1 ≤ Q ≤ 10,000)가 주어진다.

다음 R개의 줄에 걸쳐 R×C 크기의 사진 정보가 주어지며, 사진의 각 픽셀에는 밝기를 의미하는 정수 K (1 ≤ K ≤ 1,000)가 주어진다.

다음 Q개의 각 줄에는 사진의 일부분을 나타내기 위한 두 꼭짓점을 의미하는 정수 r1, c1, r2, c2 (1 ≤ r1 ≤ r2 ≤ R, 1 ≤ c1 ≤ c2 ≤ C)가 주어진다.

출력

Q개의 각 줄에 주어진 사진에서 두 점 (r1, c1)과 (r2, c2)를 꼭짓점으로 하는 직사각형의 밝기 평균을 출력한다. 평균은 정수 나눗셈으로 몫만 취한다.

예제 입력 1

5 6 1
4 1 3 4 9 5
1 2 8 7 5 5
8 1 2 5 3 2
1 5 3 4 2 5
5 2 1 2 3 5
2 2 4 5

예제 출력 1

3

예제 입력 2

4 3 5
25 93 64
10 29 85
80 63 71
99 58 86
2 2 2 3
3 2 3 3
1 2 2 2
1 2 4 3
2 3 2 3

예제 출력 2

57
67
61
68
85

알고리즘 분류

누적 합

코드

R, C, Q = map(int, input().split())
pic = []
dp = [[0 for _ in range(C + 1)] for _ in range(R + 1)] # 누적합을 담을 배열
for _ in range(R):
    pic.append(list(map(int, input().split())))

for i in range(1, R + 1):
    for j in range(1, C + 1):
        # dp 누적합 공식 세우기
        dp[i][j] = -dp[i-1][j-1] + dp[i-1][j] + dp[i][j-1] + pic[i-1][j-1]

for j in range(Q):
    r1, c1, r2, c2 =  map(int, input().split())
    ans = dp[r2][c2] - dp[r1-1][c2] - dp[r2][c1-1] + dp[r1-1][c1-1] # 부분 밝기
    num = ((r2 - r1) + 1) * ((c2 - c1) + 1) # 부분 넓이
    print(ans // num)

---

🔮 백준 1495. 기타리스트

문제

Day Of Mourning의 기타리스트 강토는 다가오는 공연에서 연주할 N개의 곡을 연주하고 있다. 지금까지 공연과는 다른 공연을 보여주기 위해서 이번 공연에서는 매번 곡이 시작하기 전에 볼륨을 바꾸고 연주하려고 한다.

먼저, 공연이 시작하기 전에 각각의 곡이 시작하기 전에 바꿀 수 있는 볼륨의 리스트를 만들었다. 이 리스트를 V라고 했을 때, V[i]는 i번째 곡을 연주하기 전에 바꿀 수 있는 볼륨을 의미한다. 항상 리스트에 적힌 차이로만 볼륨을 바꿀 수 있다. 즉, 현재 볼륨이 P이고 지금 i번째 곡을 연주하기 전이라면, i번 곡은 P+V[i]나 P-V[i] 로 연주해야 한다. 하지만, 0보다 작은 값으로 볼륨을 바꾸거나, M보다 큰 값으로 볼륨을 바꿀 수 없다.

곡의 개수 N과 시작 볼륨 S, 그리고 M이 주어졌을 때, 마지막 곡을 연주할 수 있는 볼륨 중 최댓값을 구하는 프로그램을 작성하시오. 모든 곡은 리스트에 적힌 순서대로 연주해야 한다.

입력

첫째 줄에 N, S, M이 주어진다. (1 ≤ N ≤ 50, 1 ≤ M ≤ 1,000, 0 ≤ S ≤ M) 둘째 줄에는 각 곡이 시작하기 전에 줄 수 있는 볼륨의 차이가 주어진다. 이 값은 1보다 크거나 같고, M보다 작거나 같다.

출력

첫째 줄에 가능한 마지막 곡의 볼륨 중 최댓값을 출력한다. 만약 마지막 곡을 연주할 수 없다면 (중간에 볼륨 조절을 할 수 없다면) -1을 출력한다.

예제 입력 1

3 5 10
5 3 7

예제 출력 1

10

예제 입력 2

4 8 20\
15 2 9 10

예제 출력 2

-1

예제 입력 3

14 40 243\
74 39 127 95 63 140 99 96 154 18 137 162 14 88

예제 출력 3

238

알고리즘 분류

• 다이나믹 프로그래밍

풀이

• N개곡 -> 매곡 볼륨 변경
• V = 볼륨리스트
• V[i] = i번째 곡을 연주하기 전에 바꿀 수 있는 볼륨
• i번 곡은 P+V[i] or P-V[i]
• 0보다 작은 값으로 볼륨을 바꾸거나, M보다 큰 값으로 볼륨을 바꿀 수 없다.
• 곡의 개수 N, 시작 볼륨 S, 볼륨 최댓값 M

코드

N, S, M = map(int, input().split())
V = list(map(int, input().split()))
answer = -1

# N행 M열 -> 각 볼륨에 대해서 가능한 모든 경우의 수를 구한다.
dp = [[0] * (M+1) for _ in range(N+1)]
dp[0][S] = 1 # 시작 값을 S로 설정

for i in range(N): # 곡 갯수만큼 탐색 (행)
    for j in range(M+1): # 최대 볼륨 내에서 탐색 (누적합이 M을 넘으면 안된다.)
        if dp[i][j] == 1: # 현재 행에 1이 존재할 때
            if j+V[i] <= M: # 누적합에 볼륨을 더했을 때 가능 여부
                    dp[i+1][j+V[i]] = 1
            if j-V[i] >= 0: # 누적합에 볼륨을 뺐을 때 가능 여부
                dp[i+1][j-V[i]] = 1

for i in range(M, -1, -1): # 최댓값을 구하기 위해 가장 큰 수인  M부터 감소시키며 탐색한다.
    if dp[N][i]==1: # 조건을 만족하는 값이 있다면 정답값에 저장
        answer = i
        break
print(answer)

🔮 15686. 치킨 배달

문제

크기가 N×N인 도시가 있다. 도시는 1×1크기의 칸으로 나누어져 있다. 도시의 각 칸은 빈 칸, 치킨집, 집 중 하나이다. 도시의 칸은 (r, c)와 같은 형태로 나타내고, r행 c열 또는 위에서부터 r번째 칸, 왼쪽에서부터 c번째 칸을 의미한다. r과 c는 1부터 시작한다.

이 도시에 사는 사람들은 치킨을 매우 좋아한다. 따라서, 사람들은 "치킨 거리"라는 말을 주로 사용한다. 치킨 거리는 집과 가장 가까운 치킨집 사이의 거리이다. 즉, 치킨 거리는 집을 기준으로 정해지며, 각각의 집은 치킨 거리를 가지고 있다. 도시의 치킨 거리는 모든 집의 치킨 거리의 합이다.

임의의 두 칸 (r1, c1)과 (r2, c2) 사이의 거리는 |r1-r2| + |c1-c2|로 구한다.

예를 들어, 아래와 같은 지도를 갖는 도시를 살펴보자.

0 2 0 1 0\
1 0 1 0 0\
0 0 0 0 0\
0 0 0 1 1\
0 0 0 1 2

0은 빈 칸, 1은 집, 2는 치킨집이다.

(2, 1)에 있는 집과 (1, 2)에 있는 치킨집과의 거리는 |2-1| + |1-2| = 2, (5, 5)에 있는 치킨집과의 거리는 |2-5| + |1-5| = 7이다. 따라서, (2, 1)에 있는 집의 치킨 거리는 2이다.

(5, 4)에 있는 집과 (1, 2)에 있는 치킨집과의 거리는 |5-1| + |4-2| = 6, (5, 5)에 있는 치킨집과의 거리는 |5-5| + |4-5| = 1이다. 따라서, (5, 4)에 있는 집의 치킨 거리는 1이다.

이 도시에 있는 치킨집은 모두 같은 프랜차이즈이다. 프렌차이즈 본사에서는 수익을 증가시키기 위해 일부 치킨집을 폐업시키려고 한다. 오랜 연구 끝에 이 도시에서 가장 수익을 많이 낼 수 있는 치킨집의 개수는 최대 M개라는 사실을 알아내었다.

도시에 있는 치킨집 중에서 최대 M개를 고르고, 나머지 치킨집은 모두 폐업시켜야 한다. 어떻게 고르면, 도시의 치킨 거리가 가장 작게 될지 구하는 프로그램을 작성하시오.

입력

첫째 줄에 N(2 ≤ N ≤ 50)과 M(1 ≤ M ≤ 13)이 주어진다.

둘째 줄부터 N개의 줄에는 도시의 정보가 주어진다.

도시의 정보는 0, 1, 2로 이루어져 있고, 0은 빈 칸, 1은 집, 2는 치킨집을 의미한다. 집의 개수는 2N개를 넘지 않으며, 적어도 1개는 존재한다. 치킨집의 개수는 M보다 크거나 같고, 13보다 작거나 같다.

출력

첫째 줄에 폐업시키지 않을 치킨집을 최대 M개를 골랐을 때, 도시의 치킨 거리의 최솟값을 출력한다.

예제 입력 1

5 3\
0 0 1 0 0\
0 0 2 0 1\
0 1 2 0 0\
0 0 1 0 0\
0 0 0 0 2

예제 출력 1

5

예제 입력 2

5 2\
0 2 0 1 0\
1 0 1 0 0\
0 0 0 0 0\
2 0 0 1 1\
2 2 0 1 2

예제 출력 2

10

예제 입력 3

5 1\
1 2 0 0 0\
1 2 0 0 0\
1 2 0 0 0\
1 2 0 0 0\
1 2 0 0 0

예제 출력 3

11

예제 입력 4

5 1\
1 2 0 2 1\
1 2 0 2 1\
1 2 0 2 1\
1 2 0 2 1\
1 2 0 2 1

예제 출력 4

32

알고리즘 분류

• 구현
• 브루트포스 알고리즘
• 백트래킹

풀이

• 치킨거리 = 집과 가장 가까운 치킨집 사이의 거리
• 도시의 치킨 거리 = 모든 집의 치킨 거리 합
• 도시의 치킨 거리 최솟값
• 0 빈칸, 1 집, 2 치킨집

코드

from itertools import combinations
N, M = map(int, input().split())
city = [list(map(int, input().split())) for _ in range(N)]
result = 10000000
house = [] # 집좌표
chicken = [] # 치킨집 좌표

for i in range(N):
    for j in range(N):
        if city[i][j] == 1:
            house.append([i, j])
        elif city[i][j] == 2:
            chicken.append([i, j])

for chi in combinations(chicken, M):  # m개의 치킨집 선택
    temp = 0            # 도시의 치킨 거리
    for h in house: 
        chi_len = 1000   # 치킨거리
        for j in range(M): # m개의 치킨 집을 모두 비교하여 최소값 구하기
            chi_len = min(chi_len, abs(h[0] - chi[j][0]) + abs(h[1] - chi[j][1]))
        temp += chi_len
    result = min(result, temp) # 경우의 수 중 가장 작은 값을 선택

print(result)

---

🔮 프로그래머스 파괴되지 않은 건물

문제 설명

[본 문제는 정확성과 효율성 테스트 각각 점수가 있는 문제입니다.]

N x M 크기의 행렬 모양의 게임 맵이 있습니다. 이 맵에는 내구도를 가진 건물이 각 칸마다 하나씩 있습니다. 적은 이 건물들을 공격하여 파괴하려고 합니다. 건물은 적의 공격을 받으면 내구도가 감소하고 내구도가 0이하가 되면 파괴됩니다. 반대로, 아군은 회복 스킬을 사용하여 건물들의 내구도를 높이려고 합니다.

적의 공격과 아군의 회복 스킬은 항상 직사각형 모양입니다.
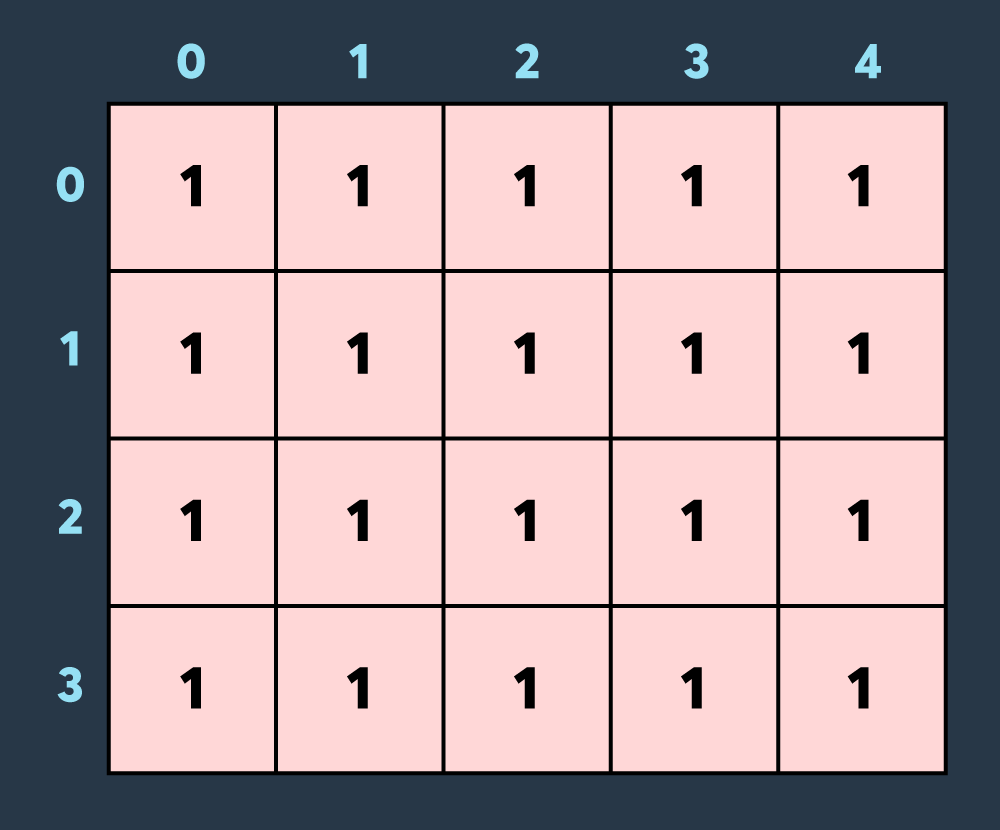
예를 들어, 아래 사진은 크기가 4 x 5인 맵에 내구도가 5인 건물들이 있는 상태입니다.

첫 번째로 적이 맵의 (0,0)부터 (3,4)까지 공격하여 4만큼 건물의 내구도를 낮추면 아래와 같은 상태가 됩니다.

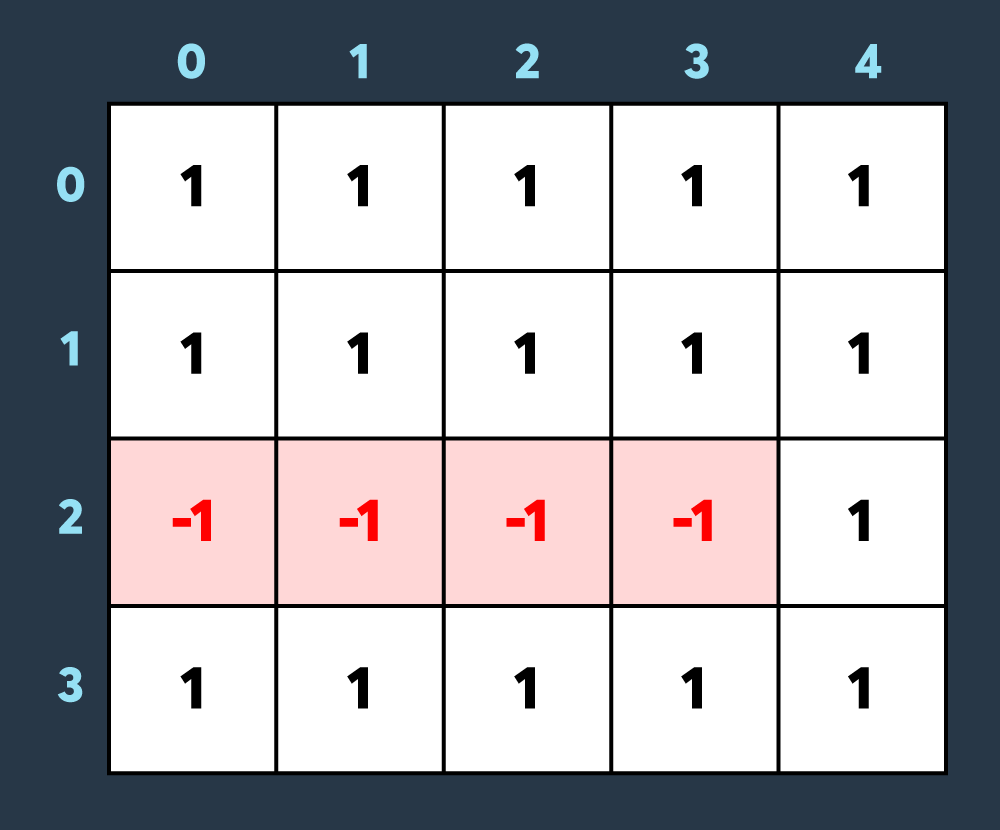
두 번째로 적이 맵의 (2,0)부터 (2,3)까지 공격하여 2만큼 건물의 내구도를 낮추면 아래와 같이 4개의 건물이 파괴되는 상태가 됩니다.

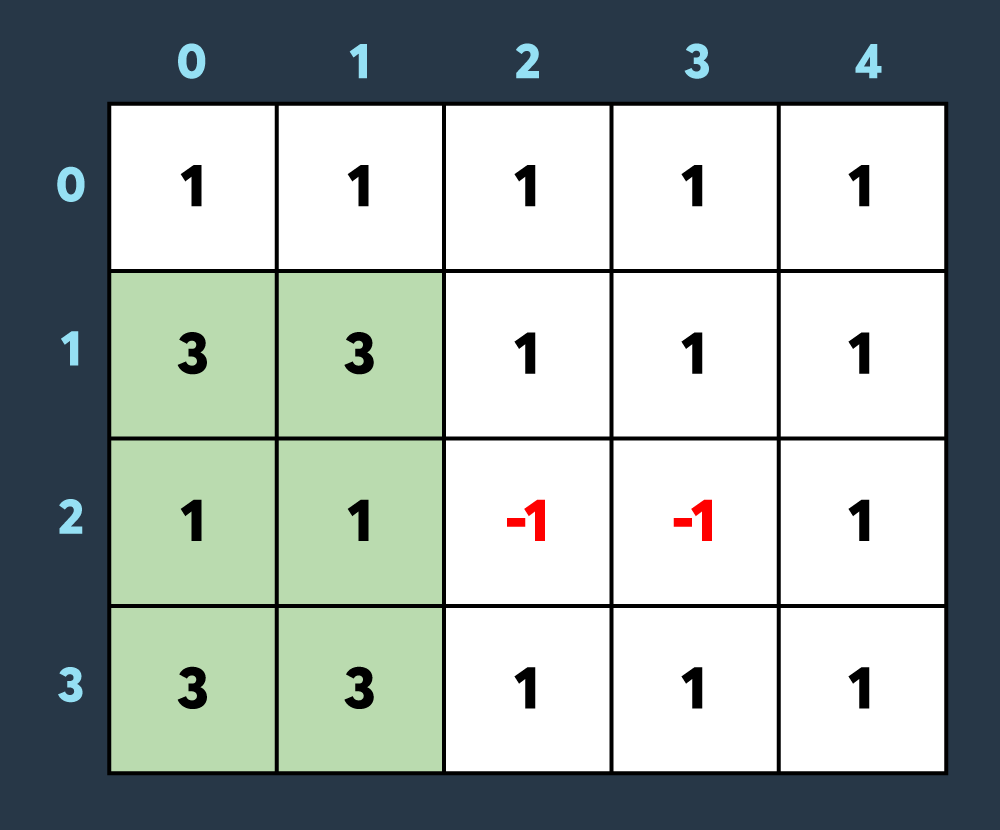
세 번째로 아군이 맵의 (1,0)부터 (3,1)까지 회복하여 2만큼 건물의 내구도를 높이면 아래와 같이 2개의 건물이 파괴되었다가 복구되고 2개의 건물만 파괴되어있는 상태가 됩니다.

마지막으로 적이 맵의 (0,1)부터 (3,3)까지 공격하여 1만큼 건물의 내구도를 낮추면 아래와 같이 8개의 건물이 더 파괴되어 총 10개의 건물이 파괴된 상태가 됩니다. (내구도가 0 이하가 된 이미 파괴된 건물도, 공격을 받으면 계속해서 내구도가 하락하는 것에 유의해주세요.)

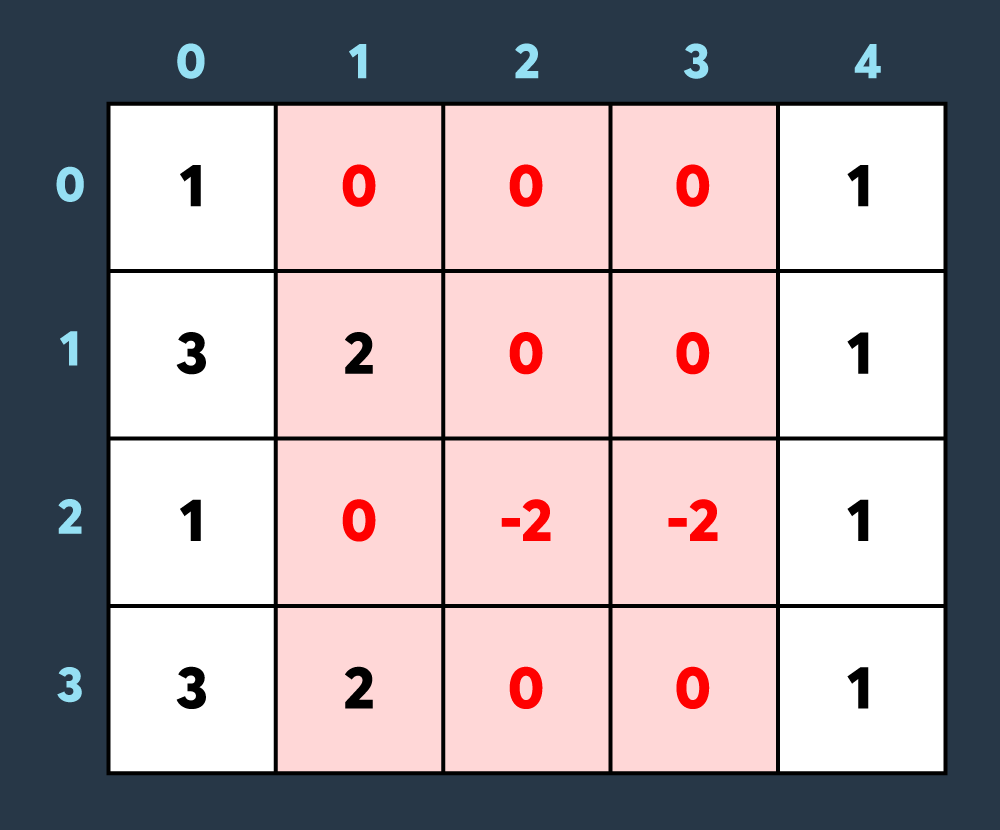
최종적으로 총 10개의 건물이 파괴되지 않았습니다.

건물의 내구도를 나타내는 2차원 정수 배열 board와 적의 공격 혹은 아군의 회복 스킬을 나타내는 2차원 정수 배열 skill이 매개변수로 주어집니다. 적의 공격 혹은 아군의 회복 스킬이 모두 끝난 뒤 파괴되지 않은 건물의 개수를 return하는 solution함수를 완성해 주세요.

제한사항

1 ≤ board의 행의 길이 (= N) ≤ 1,000
1 ≤ board의 열의 길이 (= M) ≤ 1,000
1 ≤ board의 원소 (각 건물의 내구도) ≤ 1,000
1 ≤ skill의 행의 길이 ≤ 250,000
skill의 열의 길이 = 6
skill의 각 행은 [type, r1, c1, r2, c2, degree]형태를 가지고 있습니다.
type은 1 혹은 2입니다.
type이 1일 경우는 적의 공격을 의미합니다. 건물의 내구도를 낮춥니다.
type이 2일 경우는 아군의 회복 스킬을 의미합니다. 건물의 내구도를 높입니다.
(r1, c1)부터 (r2, c2)까지 직사각형 모양의 범위 안에 있는 건물의 내구도를 degree 만큼 낮추거나 높인다는 뜻입니다.
0 ≤ r1 ≤ r2 < board의 행의 길이
0 ≤ c1 ≤ c2 < board의 열의 길이
1 ≤ degree ≤ 500
type이 1이면 degree만큼 건물의 내구도를 낮춥니다.
type이 2이면 degree만큼 건물의 내구도를 높입니다.
건물은 파괴되었다가 회복 스킬을 받아 내구도가 1이상이 되면 파괴되지 않은 상태가 됩니다. 즉, 최종적으로 건물의 내구도가 1이상이면 파괴되지 않은 건물입니다.
정확성 테스트 케이스 제한 사항
1 ≤ board의 행의 길이 (= N) ≤ 100
1 ≤ board의 열의 길이 (= M) ≤ 100
1 ≤ board의 원소 (각 건물의 내구도) ≤ 100
1 ≤ skill의 행의 길이 ≤ 100
1 ≤ degree ≤ 100
효율성 테스트 케이스 제한 사항
주어진 조건 외 추가 제한사항 없습니다.

입출력 예

board skill result
[[5,5,5,5,5],[5,5,5,5,5],[5,5,5,5,5],[5,5,5,5,5]] [[1,0,0,3,4,4],[1,2,0,2,3,2],[2,1,0,3,1,2],[1,0,1,3,3,1]] 10
[[1,2,3],[4,5,6],[7,8,9]] [[1,1,1,2,2,4],[1,0,0,1,1,2],[2,2,0,2,0,100]] 6

입출력 예 설명

입출력 예 #1

문제 예시와 같습니다.

입출력 예 #2

<초기 맵 상태>

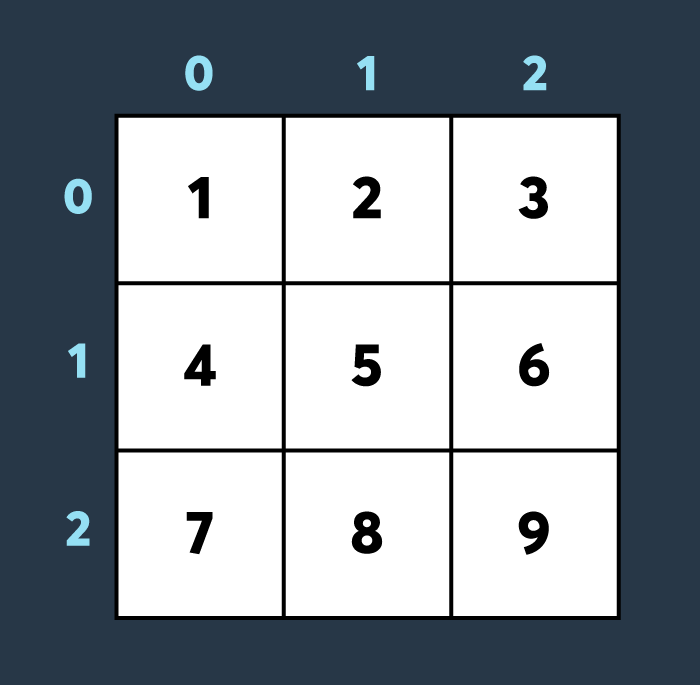
첫 번째로 적이 맵의 (1,1)부터 (2,2)까지 공격하여 4만큼 건물의 내구도를 낮추면 아래와 같은 상태가 됩니다.

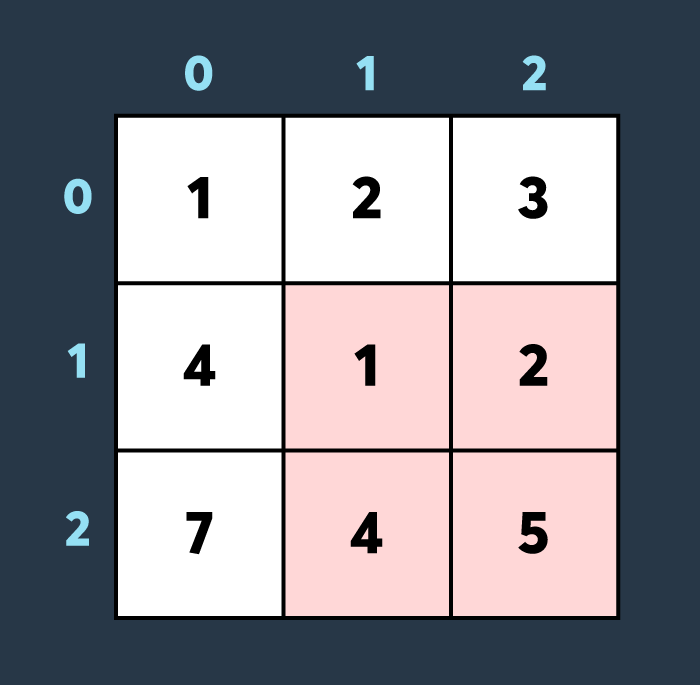
두 번째로 적이 맵의 (0,0)부터 (1,1)까지 공격하여 2만큼 건물의 내구도를 낮추면 아래와 같은 상태가 됩니다.

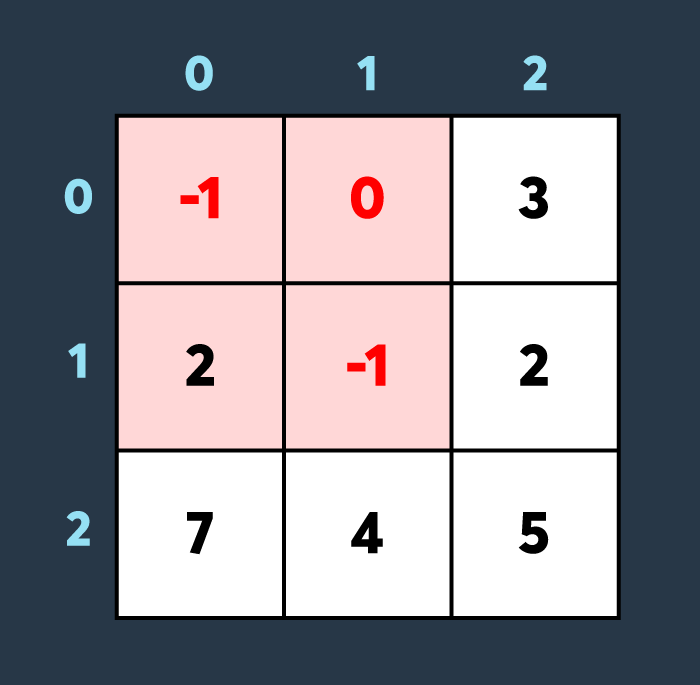
마지막으로 아군이 맵의 (2,0)부터 (2,0)까지 회복하여 100만큼 건물의 내구도를 높이면 아래와 같은 상황이 됩니다.

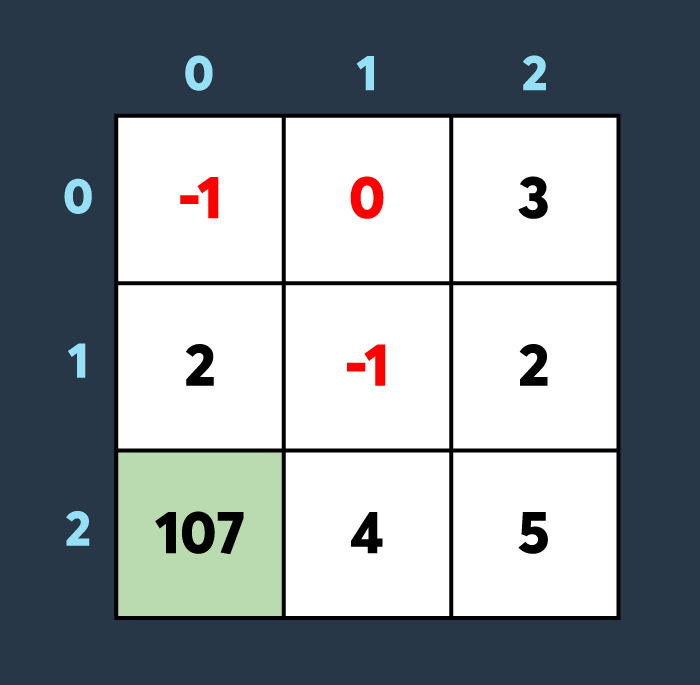
총, 6개의 건물이 파괴되지 않았습니다. 따라서 6을 return 해야 합니다.

풀이

• maybe 누적합?