[알고리즘A] 8회차: 0522-0529

최정윤·2023년 5월 29일

알고리즘

목록 보기

12/41

🥙 1992. 쿼드트리

문제

흑백 영상을 압축하여 표현하는 데이터 구조로 쿼드 트리(Quad Tree)라는 방법이 있다. 흰 점을 나타내는 0과 검은 점을 나타내는 1로만 이루어진 영상(2차원 배열)에서 같은 숫자의 점들이 한 곳에 많이 몰려있으면, 쿼드 트리에서는 이를 압축하여 간단히 표현할 수 있다.

주어진 영상이 모두 0으로만 되어 있으면 압축 결과는 "0"이 되고, 모두 1로만 되어 있으면 압축 결과는 "1"이 된다. 만약 0과 1이 섞여 있으면 전체를 한 번에 나타내지를 못하고, 왼쪽 위, 오른쪽 위, 왼쪽 아래, 오른쪽 아래, 이렇게 4개의 영상으로 나누어 압축하게 되며, 이 4개의 영역을 압축한 결과를 차례대로 괄호 안에 묶어서 표현한다

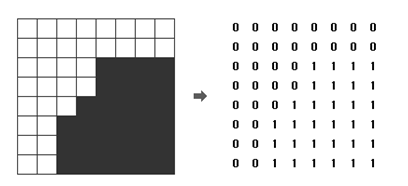
위 그림에서 왼쪽의 영상은 오른쪽의 배열과 같이 숫자로 주어지며, 이 영상을 쿼드 트리 구조를 이용하여 압축하면 "(0(0011)(0(0111)01)1)"로 표현된다. N ×N 크기의 영상이 주어질 때, 이 영상을 압축한 결과를 출력하는 프로그램을 작성하시오.

입력

첫째 줄에는 영상의 크기를 나타내는 숫자 N 이 주어진다. N 은 언제나 2의 제곱수로 주어지며, 1 ≤ N ≤ 64의 범위를 가진다. 두 번째 줄부터는 길이 N의 문자열이 N개 들어온다. 각 문자열은 0 또는 1의 숫자로 이루어져 있으며, 영상의 각 점들을 나타낸다.

출력

영상을 압축한 결과를 출력한다.

예제 입력 1

8
11110000
11110000
00011100
00011100
11110000
11110000
11110011
11110011

예제 출력 1

((110(0101))(0010)1(0001))

알고리즘 및 풀이

분할 정복
재귀
2차원배열을 절반씩 나누어가며 탐색을 진행한다.
https://velog.io/@shinhojung814/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-WEEK-02-%EB%B6%84%ED%95%A0-%EC%A0%95%EB%B3%B5-%EB%AC%B8%EC%A0%9C%ED%92%80%EC%9D%B4

코드

# 쿼드트리 함수 작성
def quad_tree(N, x, y):
    global arr
    vertex = arr[x][y] # 탐색을 위한 vertex 선언
    
    # 재귀 순환
    for i in range(x, x + N):
        for j in range(y, y + N):
            if vertex != arr[i][j]: # 한 섹션의 수가 하나로 통일되지 않아있을 때
                print('(',end='')
                quad_tree(N // 2, x, y) # 왼쪽 위
                quad_tree(N // 2, x, y + N // 2) # 오른쪽 위
                quad_tree(N // 2, x + N // 2, y) # 왼쪽 아래
                quad_tree(N // 2, x + N // 2, y + N // 2) # 오른쪽 아래
                print(')',end='')
                return
            
    print(vertex,end='') # 재귀 한바퀴 돌 때마다 출력

# 입력값 받기
N = int(input())
arr = []
for i in range(N):
    arr.append(list(input()))
    
quad_tree(N, 0, 0)

🥙 16974. 레벨 햄버거

문제

상근날드에서 오랜만에 새로운 햄버거를 출시했다. 바로 레벨-L 버거이다. 레벨-L 버거는 다음과 같이 만든다.

레벨-0 버거는 패티만으로 이루어져 있다.
레벨-L 버거는 햄버거번, 레벨-(L-1) 버거, 패티, 레벨-(L-1)버거, 햄버거번으로 이루어져 있다. (L ≥ 1)

예를 들어, 레벨-1 버거는 'BPPPB', 레벨-2 버거는 'BBPPPBPBPPPBB'와 같이 생겼다. (B는 햄버거번, P는 패티)

상도가 상근날드에 방문해서 레벨-N 버거를 시켰다. 상도가 햄버거의 아래 X장을 먹었을 때, 먹은 패티는 몇 장일까? 한 장은 햄버거번 또는 패티 한 장이다.

입력

첫째 줄에 N과 X가 주어진다.

출력

첫째 줄에 상도가 먹은 패티의 수를 출력한다.

제한

1 ≤ N ≤ 50
1 ≤ X ≤ 레벨-N 버거에 있는 레이어의 수

예제 입력 1

2 7

예제 출력 1

예제 입력 2

1 1

예제 출력 2

예제 입력 3

50 4321098765432109

예제 출력 3

2160549382716056

알고리즘 분류 및 풀이

다이나믹 프로그래밍
분할 정복
재귀
레벨-L = B(레벨-(L-1))P(레벨-(L-1))B

🥙 11729. 하노이 탑 이동 순서

문제

세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로 옮기려 한다.

한 번에 한 개의 원판만을 다른 탑으로 옮길 수 있다.
쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다.
이 작업을 수행하는데 필요한 이동 순서를 출력하는 프로그램을 작성하라. 단, 이동 횟수는 최소가 되어야 한다.

아래 그림은 원판이 5개인 경우의 예시이다.

입력

첫째 줄에 첫 번째 장대에 쌓인 원판의 개수 N (1 ≤ N ≤ 20)이 주어진다.

출력

첫째 줄에 옮긴 횟수 K를 출력한다.

두 번째 줄부터 수행 과정을 출력한다. 두 번째 줄부터 K개의 줄에 걸쳐 두 정수 A B를 빈칸을 사이에 두고 출력하는데, 이는 A번째 탑의 가장 위에 있는 원판을 B번째 탑의 가장 위로 옮긴다는 뜻이다.

예제 입력 1

예제 출력 1

7
1 3
1 2
3 2
1 3
2 1
2 3
1 3

알고리즘 및 풀이

재귀
이동횟수 = 2**n - 1
1 -> 3 하려면 n-1개의 원판을 2기둥으로 옮겨야 한다. -> 이를 재귀적으로 표현

코드

def hanoi(n, start, end):
    tmp = 6 - start - end # start 기둥과 end 기둥을 제외한 나머지 하나의 기둥
    if n == 0:
        return
    hanoi(n-1, start, tmp) # n-1개 원판을 start -> tmp 로 이동
    print(start, end)
    hanoi(n-1, tmp, end) # start-> end로 1개의 원판 옮기고 tmp -> end로 n-1개의 원판을 옮긴다.
    
n = int(input())
print(2**n - 1)
hanoi(n, 1, 3)

🥙 1074. Z

문제

한수는 크기가 2N × 2N인 2차원 배열을 Z모양으로 탐색하려고 한다. 예를 들어, 2×2배열을 왼쪽 위칸, 오른쪽 위칸, 왼쪽 아래칸, 오른쪽 아래칸 순서대로 방문하면 Z모양이다.

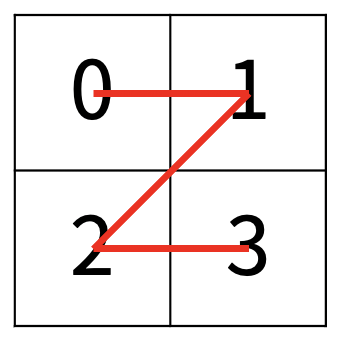
N > 1인 경우, 배열을 크기가 2N-1 × 2N-1로 4등분 한 후에 재귀적으로 순서대로 방문한다.

다음 예는 22 × 22 크기의 배열을 방문한 순서이다.

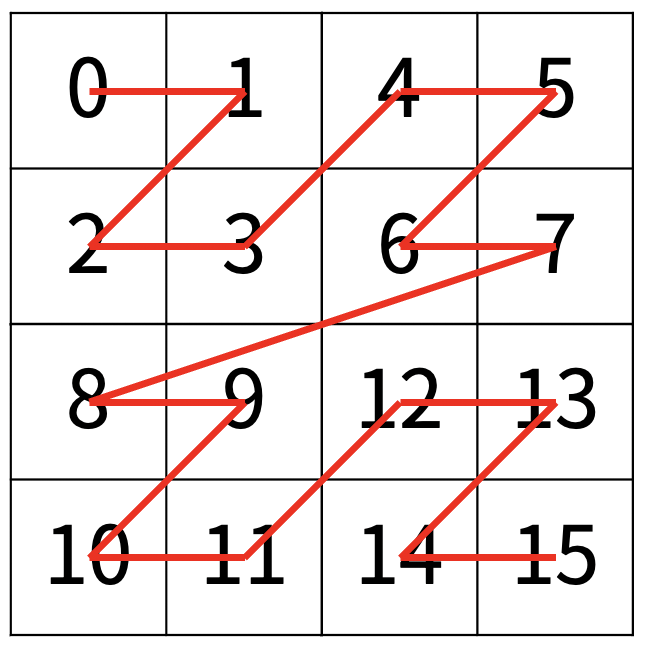
N이 주어졌을 때, r행 c열을 몇 번째로 방문하는지 출력하는 프로그램을 작성하시오.

다음은 N=3일 때의 예이다.

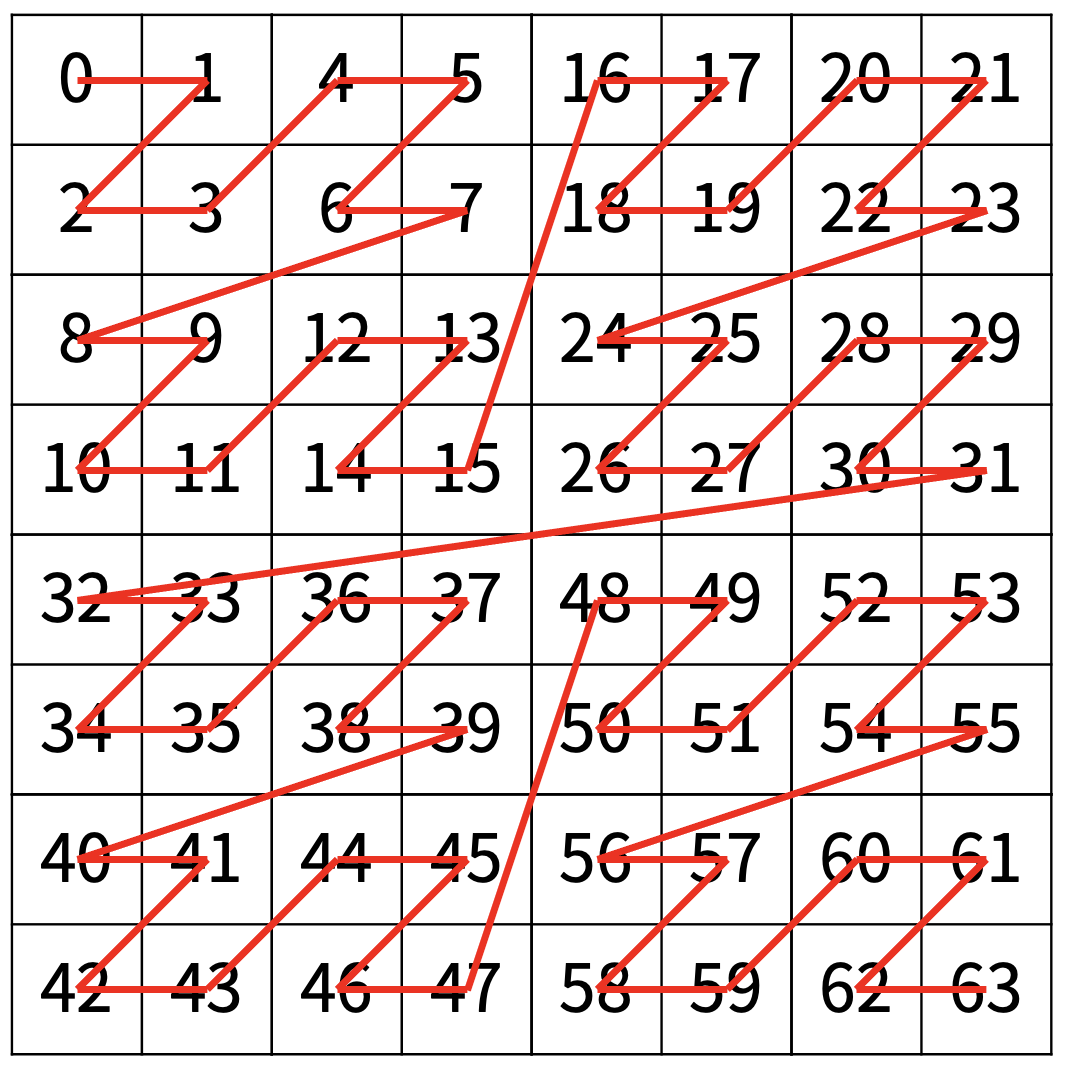
입력

첫째 줄에 정수 N, r, c가 주어진다.

출력

r행 c열을 몇 번째로 방문했는지 출력한다.

제한

1 ≤ N ≤ 15
0 ≤ r, c < 2N

예제 입력 1

2 3 1

예제 출력 1

예제 입력 2

3 7 7

예제 출력 2

예제 입력 3

1 0 0

예제 출력 3

예제 입력 4

4 7 7

예제 출력 4

예제 입력 5

10 511 511

예제 출력 5

262143

예제 입력 6

10 512 512

예제 출력 6

786432

알고리즘 및 풀이

분할 정복
재귀
한 섹션씩 늘어날때 마다 2의N승 만큼 증가한다.

코드

# 입력값 받기
N, r, c = map(int, input().split())

answer = 0

while N != 0: # 반복 1회당 큰 Z 하나 완성

    N -= 1 # 좌표를 절반으로 나누어 탐색

    # 왼쪽 위
    if r < 2 ** N and c < 2 ** N:
        answer += ( 2 ** N ) * ( 2 ** N ) * 0

    # 오른쪽 위
    elif r < 2 ** N and c >= 2 ** N: 
        answer += ( 2 ** N ) * ( 2 ** N ) * 1
        c -= ( 2 ** N )
        
    # 왼쪽 아래  
    elif r >= 2 ** N and c < 2 ** N: 
        answer += ( 2 ** N ) * ( 2 ** N ) * 2
        r -= ( 2 ** N )
        
    # 오른쪽 아래  
    else:
        answer += ( 2 ** N ) * ( 2 ** N ) * 3
        r -= ( 2 ** N )
        c -= ( 2 ** N )
    
print(answer)

🥙 1802. 종이 접기

문제

동호는 종이를 접는데 옆에서 보고 접으려고 한다. 옆에서 본다는 말은 아래 그림과 같이 본다는 뜻이다. 동호는 종이를 반으로 접을 때, 아래와 같이 두가지중 하나로만 접을 수 있다.

오른쪽 반을 반시계 방향으로 접어서 왼쪽 반의 위로 접는다.
오른쪽 반을 시계 방향으로 접어서 왼쪽 반의 아래로 접는다.
아래의 그림은 위의 설명을 그림으로 옮긴 것이다.

한 번의 종이 접기가 끝났을 때, 동호는 종이 접기를 원하는 만큼 더 할 수 있다. 종이 접기를 한번 접을 때 마다 두께는 2배가 되고 길이는 절반이 될 것이다.

종이 접기를 여러 번 했을 때 (안접을 수도 있다), 동호는 종이를 다시 피기로 했다. 그러고 나서 다시 접고 이렇게 놀고 있었다. 옆에서 보고 있던 원룡이는 동호를 위해 종이를 접어서 주기로 했다.(원룡이는 동호의 규칙대로 접지 않는다.) 동호는 그리고 나서 원룡이가 접었다 핀 종이를 다시 동호의 규칙대로 접을 수 있는지 궁금해졌다.

위의 저 종이를 접었다 피면 다음과 같은 그림처럼 펴진다.

종이가 시계방향으로 꺽여있으면 OUT이고, 반시계방향으로 꺾여있으면 IN이다.

종이가 접혀있는 정보가 왼쪽부터 오른쪽까지 차례대로 주어졌을 때, 이 종이를 동호의 규칙대로 접을 수 있는지 없는지를 구하는 프로그램을 작성하시오.

입력

첫째 줄에 테스트 케이스의 개수 T가 주어진다. T는 1000보다 작거나 같은 자연수이다. 둘째 줄부터 T개의 줄에 각각의 종이가 어떻게 접혀있는지가 주어진다. 종이의 정보는 문자열로 주어지며, 1은 위의 그림에서 OUT을 의미하고 0은 위의 그림에서 IN을 의미한다. 예를 들어, 위의 그림과 같은 모양은 100으로 나타낼 수 있다. 문자열의 길이는 3000보다 작으며, 항상 2N-1꼴이다. (N ≥ 1)

출력

T개의 줄에 차례대로 각각의 종이를 동호의 방법대로 다시 접을 수 있으면 YES를, 접을 수 없으면 NO를 출력한다.

예제 입력 1

3
0
000
1000110

예제 출력 1

YES
NO
YES

최정윤

개발 기록장

이전 포스트

[알고리즘A] 8회차: 0522-0529

알고리즘

🥙 1992. 쿼드트리

문제

입력

출력

예제 입력 1

예제 출력 1

알고리즘 및 풀이

코드

🥙 16974. 레벨 햄버거

문제

입력

출력

제한

예제 입력 1

예제 출력 1

예제 입력 2

예제 출력 2

예제 입력 3

예제 출력 3

알고리즘 분류 및 풀이

🥙 11729. 하노이 탑 이동 순서

문제

입력

출력

예제 입력 1

예제 출력 1

알고리즘 및 풀이

코드

🥙 1074. Z

문제

입력

출력

제한

예제 입력 1

예제 출력 1

예제 입력 2

예제 출력 2

예제 입력 3

예제 출력 3

예제 입력 4

예제 출력 4

예제 입력 5

예제 출력 5

예제 입력 6

예제 출력 6

알고리즘 및 풀이

코드

🥙 1802. 종이 접기

문제

입력

출력

예제 입력 1

예제 출력 1

[알고리즘A] 7회차: 0424-0430

0개의 댓글