🥁 프로그래머스 154538. 숫자 변환하기
문제 설명
자연수 x를 y로 변환하려고 합니다. 사용할 수 있는 연산은 다음과 같습니다.
x에 n을 더합니다
x에 2를 곱합니다.
x에 3을 곱합니다.
자연수 x, y, n이 매개변수로 주어질 때, x를 y로 변환하기 위해 필요한 최소 연산 횟수를 return하도록 solution 함수를 완성해주세요. 이때 x를 y로 만들 수 없다면 -1을 return 해주세요.
제한사항
1 ≤ x ≤ y ≤ 1,000,000
1 ≤ n < y
입출력 예
x y n result
10 40 5 2
10 40 30 1
2 5 4 -1
입출력 예 #1
x에 2를 2번 곱하면 40이 되고 이때가 최소 횟수입니다.
입출력 예 #2
x에 n인 30을 1번 더하면 40이 되고 이때가 최소 횟수입니다.
입출력 예 #3
x를 y로 변환할 수 없기 때문에 -1을 return합니다.
알고리즘 분류
- bfs
코드
from collections import deque
def solution(x, y, n):
dis = [0 for _ in range(y+1)] # 연산횟수
Q = deque()
Q.append(x)
if x == y: # 두 수가 같다면 연산 필요 x
return 0
while Q: # Q가 존재하는 동안
nx = Q.popleft()
for dir in range(3): # 세가지 연산중 하나
if dir == 0:
cur_x = nx * 2
if dir == 1:
cur_x = nx * 3
if dir == 2:
cur_x = nx + n
if cur_x > y or dis[cur_x]: # x가 y보다 클 때
continue
if cur_x == y: # 연산결과가 y와 일치할 때
return dis[nx] + 1 # 연산횟수 반환
Q.append(cur_x) # 큐에 연산결과 저장
dis[cur_x] = dis[nx] + 1 # 연산횟수 저장
return -1 # return 조건 만족하지 않으면 -1🥁 프로그래머스 12900. 2 x n 타일링
문제 설명
가로 길이가 2이고 세로의 길이가 1인 직사각형모양의 타일이 있습니다. 이 직사각형 타일을 이용하여 세로의 길이가 2이고 가로의 길이가 n인 바닥을 가득 채우려고 합니다. 타일을 채울 때는 다음과 같이 2가지 방법이 있습니다.
타일을 가로로 배치 하는 경우
타일을 세로로 배치 하는 경우
예를들어서 n이 7인 직사각형은 다음과 같이 채울 수 있습니다.

직사각형의 가로의 길이 n이 매개변수로 주어질 때, 이 직사각형을 채우는 방법의 수를 return 하는 solution 함수를 완성해주세요.
제한사항
가로의 길이 n은 60,000이하의 자연수 입니다.
경우의 수가 많아 질 수 있으므로, 경우의 수를 1,000,000,007으로 나눈 나머지를 return해주세요.
입출력 예
n result
4 5
입출력 예 #1
다음과 같이 5가지 방법이 있다.





풀이
n = 1: 1 -> 1
n = 2: 11, 2 -> 2
n = 3: 111, 21, 12 -> 3
n = 4: 1111, 211, 112, 121, 22 -> 5
코드
def solution(n):
dp = [0 for i in range(n)]
dp[0], dp[1] = 1, 2
for i in range(2, n):
dp[i] = (dp[i-1] + dp[i-2]) % 1000000007
return dp[n-1]🥁 프로그래머스 77885. 2개 이하로 다른 비트
문제 설명
양의 정수 x에 대한 함수 f(x)를 다음과 같이 정의합니다.
x보다 크고 x와 비트가 1~2개 다른 수들 중에서 제일 작은 수
예를 들어,
f(2) = 3 입니다. 다음 표와 같이 2보다 큰 수들 중에서 비트가 다른 지점이 2개 이하이면서 제일 작은 수가 3이기 때문입니다.
수 비트 다른 비트의 개수
2 000...0010
3 000...0011 1
f(7) = 11 입니다. 다음 표와 같이 7보다 큰 수들 중에서 비트가 다른 지점이 2개 이하이면서 제일 작은 수가 11이기 때문입니다.
수 비트 다른 비트의 개수
7 000...0111
8 000...1000 4
9 000...1001 3
10 000...1010 3
11 000...1011 2
정수들이 담긴 배열 numbers가 매개변수로 주어집니다. numbers의 모든 수들에 대하여 각 수의 f 값을 배열에 차례대로 담아 return 하도록 solution 함수를 완성해주세요.
제한사항
1 ≤ numbers의 길이 ≤ 100,000
0 ≤ numbers의 모든 수 ≤ 1015
입출력 예
numbers result
[2,7][3,11]
코드
def solution(numbers):
answer = []
for number in numbers:
bin_number = list('0' + bin(number)[2:]) # 이진수로 변경 후 앞 '0b' 슬라이싱 하여 저장
idx = ''.join(bin_number).rfind('0') # 리스트에서 가장 오른쪽에 있는 0의 인덱스를 탐색
bin_number[idx] = '1' # idx에 해당하는 위치의 0을 1로 변경
if number % 2 == 1: # 홀수일 때
bin_number[idx+1] = '0' # 가장 오른쪽의 1을 0으로 변경
answer.append(int(''.join(bin_number), 2)) # 이진수를 다시 10진수로 바꿔 저장
return answer🥁 프로그래머스 68645. 삼각 달팽이 (오답)
문제 설명
정수 n이 매개변수로 주어집니다. 다음 그림과 같이 밑변의 길이와 높이가 n인 삼각형에서 맨 위 꼭짓점부터 반시계 방향으로 달팽이 채우기를 진행한 후, 첫 행부터 마지막 행까지 모두 순서대로 합친 새로운 배열을 return 하도록 solution 함수를 완성해주세요.
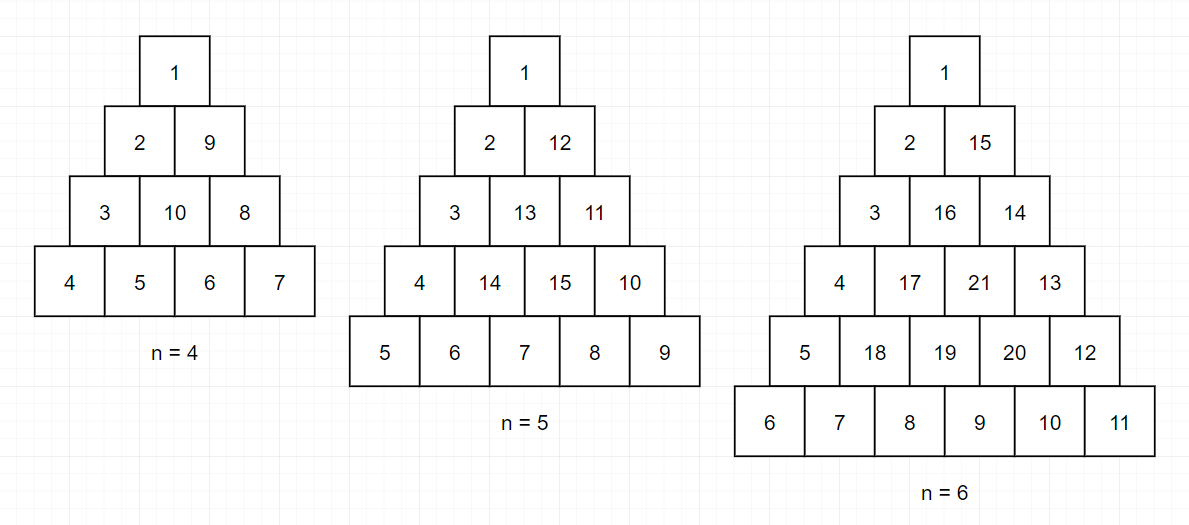
제한사항
n은 1 이상 1,000 이하입니다.
입출력 예
n result
4 [1,2,9,3,10,8,4,5,6,7]
5 [1,2,12,3,13,11,4,14,15,10,5,6,7,8,9]
6 [1,2,15,3,16,14,4,17,21,13,5,18,19,20,12,6,7,8,9,10,11]
코드
def solution(n):
answer = [[0 for j in range(1, i+1)] for i in range(1, n+1)] # 삼각형 구조 만들기
x, y = -1, 0 # 좌표 초기화 => 처음 시작은 아래로 내려가기 때문에 x = -1
num = 1
for i in range(n): # 방향
for j in range(i, n): # 좌표 구하기
if i % 3 == 0: # 하
x += 1
elif i % 3 == 1: # 우
y += 1
else: # 상
x -= 1
y -= 1
answer[x][y] = num
num += 1
return sum(answer, []) # 2차원리스트 1차원 리스트로 변환🥁 프로그래머스 42883. 큰 수 만들기
문제 설명
어떤 숫자에서 k개의 수를 제거했을 때 얻을 수 있는 가장 큰 숫자를 구하려 합니다.
예를 들어, 숫자 1924에서 수 두 개를 제거하면 [19, 12, 14, 92, 94, 24] 를 만들 수 있습니다. 이 중 가장 큰 숫자는 94 입니다.
문자열 형식으로 숫자 number와 제거할 수의 개수 k가 solution 함수의 매개변수로 주어집니다. number에서 k 개의 수를 제거했을 때 만들 수 있는 수 중 가장 큰 숫자를 문자열 형태로 return 하도록 solution 함수를 완성하세요.
제한 조건
number는 2자리 이상, 1,000,000자리 이하인 숫자입니다.
k는 1 이상 number의 자릿수 미만인 자연수입니다.
입출력 예
number k return
"1924" 2 "94"
"1231234" 3 "3234"
"4177252841" 4 "775841"
코드
def solution(number, k):
answer = [] # Stack
for num in number:
if not answer: # 스택이 비어있는 경우
answer.append(num)
continue
if k > 0:
while answer[-1] < num: # 스택의 맨 끝수가 새로운 수보다 작으면
answer.pop() # 제거
k -= 1 # 횟수 차감
if not answer or k <= 0: # 스택이 비어있거나 횟수가 모두 차감되면 종료
break
answer.append(num) # 새로운 수 스택에 저장
if k > 0:
answer = answer[:-k] # 끝 수부터 차례대로 k개만큼 슬라이싱
return ''.join(answer)