🍘 11725. 트리의 부모 찾기

문제

루트 없는 트리가 주어진다. 이때, 트리의 루트를 1이라고 정했을 때, 각 노드의 부모를 구하는 프로그램을 작성하시오.

입력

첫째 줄에 노드의 개수 N (2 ≤ N ≤ 100,000)이 주어진다. 둘째 줄부터 N-1개의 줄에 트리 상에서 연결된 두 정점이 주어진다.

출력

첫째 줄부터 N-1개의 줄에 각 노드의 부모 노드 번호를 2번 노드부터 순서대로 출력한다.

예제 입력 1

7
1 6
6 3
3 5
4 1
2 4
4 7

예제 출력 1

4
6
1
3
1
4

예제 입력 2

12
1 2
1 3
2 4
3 5
3 6
4 7
4 8
5 9
5 10
6 11
6 12

예제 출력 2

1
1
2
3
3
4
4
5
5
6
6

알고리즘 분류

• 그래프 이론
• 그래프 탐색
• 트리
• 너비 우선 탐색
• 깊이 우선 탐색

코드 - python3 런타임에러 / pypy3 런타임에러

import sys
input = sys.stdin.readline

# N 입력
N = int(input())

# tree, parent 초기화
tree = [[] for _ in range(N + 1)] # 해당 인덱스의 노드와 연결되어 있는 자식노드 저장
parent = [None for _ in range(N + 1)]

# DFS
def DFS(graph, vertex, visited):
    # 트리를 순환하며 탐색
    for i in graph[vertex]:
        # 만약 방문하지 않았을 경우 방문할 정점의 값을 할당하고 재귀함수 호출
        if not visited[i]:
            visited[i] = vertex
            DFS(graph, i, visited)

# 주어진 노드로 트리 값 할당
for _ in range(N - 1):
    node_a, node_b = map(int, input().split())
    tree[node_a].append(node_b)
    tree[node_b].append(node_a)

# DFS 함수 사용하여 parent 값 할당
DFS(tree, 1, parent)

# 각 노드의 부모 노드 번호를 2번부터 순서대로 출력
for i in range(2, N + 1):
    print(parent[i])

---

🍘 1189. 컴백홈

문제

한수는 캠프를 마치고 집에 돌아가려 한다. 한수는 현재 왼쪽 아래점에 있고 집은 오른쪽 위에 있다. 그리고 한수는 집에 돌아가는 방법이 다양하다. 단, 한수는 똑똑하여 한번 지나친 곳을 다시 방문하지는 않는다.

  cdef  ...f  ..ef  ..gh  cdeh  cdej  ...f 
  bT..  .T.e  .Td.  .Tfe  bTfg  bTfi  .Tde 
  a...  abcd  abc.  abcd  a...  a.gh  abc. 

거리 : 6 6 6 8 8 10 6
위 예제는 한수가 집에 돌아갈 수 있는 모든 경우를 나타낸 것이다. T로 표시된 부분은 가지 못하는 부분이다. 문제는 R x C 맵에 못가는 부분이 주어지고 거리 K가 주어지면 한수가 집까지도 도착하는 경우 중 거리가 K인 가짓수를 구하는 것이다.

입력

첫 줄에 정수 R(1 ≤ R ≤ 5), C(1 ≤ C ≤ 5), K(1 ≤ K ≤ R×C)가 공백으로 구분되어 주어진다. 두 번째부터 R+1번째 줄까지는 R×C 맵의 정보를 나타내는 '.'과 'T'로 구성된 길이가 C인 문자열이 주어진다.

출력

첫 줄에 거리가 K인 가짓수를 출력한다.

예제 입력 1

3 4 6
....
.T..
....

예제 출력 1

4

알고리즘 분류

• 그래프 이론
• 브루트포스 알고리즘
• 그래프 탐색
• 깊이 우선 탐색
• 백트래킹

코드 - python3 성공

import sys
input = sys.stdin.readline

# r X c  맵
# 거리가 k 인 가짓수 구하기
r,c,k = map(int, input().split())
graph = []
for _ in range(r):
    graph.append(list(input().rstrip()))

dx = [1,-1,0,0]
dy = [0,0,1,-1]

answer = 0
def dfs(x,y,distance):
    global answer
    # 목표 도착 지점 : (0,c-1)
    # 목표 거리 : k
    # 목표거리에 해당하면 정답값에 카운팅
    if distance == k and y == c-1 and x==0:
        answer += 1
    else:
        # T로 방문처리
        graph[x][y]='T'
        for i in range(4): # 방향 정하기
            nx = x+dx[i]
            ny = y+dy[i]
            # 백트래킹 한정 조건 : 이동 위치가 경로 내부에 있고 T가 아닐때
            if(0 <= nx < r and 0 <= ny < c and graph[nx][ny] == '.'):
                graph[nx][ny]='T' # 방문처리
                dfs(nx,ny,distance+1)
                # 재귀를 다 돌면 원래 상태로 돌려 놓아 다른 방향으로 다시 탐색하도록 한다.
                graph[nx][ny]='.'

# 시작점 : (r-1,0)
# 초기 distance : 1
dfs(r-1,0,1)
# 정답
print(answer)

---

🍘 1527. 금민수의 개수

문제

은민이는 4와 7을 좋아하고, 나머지 숫자는 싫어한다. 금민수는 어떤 수가 4와 7로만 이루어진 수를 말한다.

A와 B가 주어졌을 때, A보다 크거나 같고, B보다 작거나 같은 자연수 중에 금민수인 것의 개수를 출력하는 프로그램을 작성하시오.

입력

첫째 줄에 A와 B가 주어진다. A는 1보다 크거나 같고, 1,000,000,000보다 작거나 같은 자연수이다. B는 A보다 크거나 같고, 1,000,000,000보다 작거나 같은 자연수이다.

출력

첫째 줄에 A보다 크거나 같고, B보다 작거나 같은 자연수 중에 금민수인 것의 개수를 출력한다.

예제 입력 1

1 10

예제 출력 1

2

예제 입력 2

11 20

예제 출력 2

0

예제 입력 3

74 77

예제 출력 3

2

예제 입력 4

1000000 5000000

예제 출력 4

64

알고리즘 분류

• 브루트포스 알고리즘

코드 - python3 성공

import sys
from itertools import product
input = sys.stdin.readline

a, b = map(int, input().split())
x = len(str(a))
y = len(str(b))

cnt = 0

for i in range(x, y+1): # x부터 y까지의 자릿수에 대해 반복문
    # product는 여러 개의 이터러블을 받아 가능한 모든 조합을 생성
    lst = list(product([4, 7], repeat=i)) # 현재 자릿수 i에 대해 4, 7의 반복 가능한 조합을 생성
    for num in lst:
        n = int(''.join(map(str, num)))
        if a <= n <= b:
            cnt += 1

print(cnt)

---

🍘 24391. 귀찮은 해강이

문제

해강이는 앙중대학교에 다닌다. 해강이는 이번 학기에 강의코드 1번부터 N번까지 N개의 강의를 듣고 있다.

모든 강의는 강의코드와 동일한 번호의 건물에서 진행된다. 예를 들어, 강의코드가 1인 강의는 1번 건물에서 진행되고, 강의코드가 N-1인 강의는 N-1번 건물에서 진행된다.

해강이는 밖에 나오는 것을 싫어해서, 강의 시간표 순서대로 모든 강의를 들으면서 한 건물에서 밖으로 나와서 다른 건물로 이동하는 횟수를 최소화하고 싶다. 앙중대학교에는 다행히도 서로 연결되어 있는 건물들이 있어, 이 건물끼리는 밖으로 나오지 않고 이동할 수 있다.

해강이의 강의 시간표가 주어질 때, 밖에 나오는 것을 싫어하는 해강이를 위해 최소 몇 번만 밖에 나오면 되는지 구해보자. 맨 처음 강의를 들으러 이동하는 횟수는 세지 않는다.

입력

첫째 줄에 강의의 개수 N(1 ≤ N ≤ 105)과 연결되어 있는 건물의 쌍의 개수 M(0 ≤ M ≤ 105)이 공백으로 구분되어 주어진다.

두 번째 줄부터는 M줄에 걸쳐 i와 j(1 ≤ i, j ≤ N)가 주어진다. 이는 i번 건물과 j번 건물이 연결되어 있다는 의미이다. 건물이 자기 자신과 연결되거나, 이미 연결된 건물의 쌍이 다시 주어지는 경우는 없다.

마지막 줄에는 N개의 강의코드 Ai(1 ≤ Ai ≤ N)로 이루어진 강의 시간표가 공백으로 구분되어 주어진다.

출력

해강이가 밖에 나와야 하는 최소 횟수를 출력한다.

예제 입력 1

5 3
1 3
2 5
3 4
1 2 3 5 4

예제 출력 1

4

알고리즘 분류

• 자료 구조
• 그래프 이론
• 그래프 탐색
• 분리 집합

코드 - python3 성공

import sys
input=sys.stdin.readline

# 서로소 집합에서 특정 원소 x의 루트 노드를 찾음
def Find(x):

    if x!=disjoint[x]:
        disjoint[x]=Find(disjoint[x])
    return disjoint[x]

def Union(a,b):

    a=Find(a)
    b=Find(b)

    # 더 큰 쪽으로 합쳐서 하나의 집합으로 만든다
    if a>b:
        disjoint[a]=b
    else:
        disjoint[b]=a

N,M=map(int,input().split())

disjoint=[0]*(N+1) # 각 원소 부모노드 저장

for i in range(1,N+1): # 건물번호 초기화
    disjoint[i]=i


for i in range(M):
    a,b=map(int,input().split())
    Union(a,b) # 합집합

L=list(map(int,input().split()))
total=0
for i in range(1,len(L)):
    if Find(L[i-1])!=Find(L[i]): # 루트 노드가 다를 때
        total+=1

print(total)

---

🍘 20055. 컨베이어 벨트 위의 로봇

문제

길이가 N인 컨베이어 벨트가 있고, 길이가 2N인 벨트가 이 컨베이어 벨트를 위아래로 감싸며 돌고 있다. 벨트는 길이 1 간격으로 2N개의 칸으로 나뉘어져 있으며, 각 칸에는 아래 그림과 같이 1부터 2N까지의 번호가 매겨져 있다.

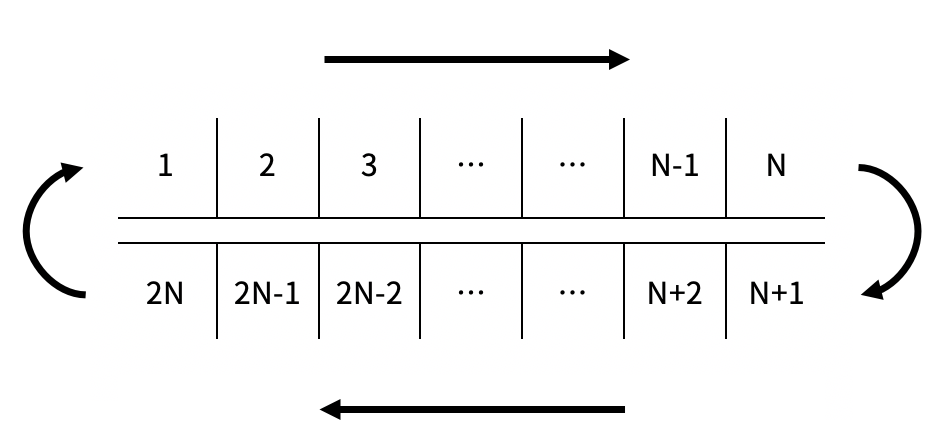
벨트가 한 칸 회전하면 1번부터 2N-1번까지의 칸은 다음 번호의 칸이 있는 위치로 이동하고, 2N번 칸은 1번 칸의 위치로 이동한다. i번 칸의 내구도는 Ai이다. 위의 그림에서 1번 칸이 있는 위치를 "올리는 위치", N번 칸이 있는 위치를 "내리는 위치"라고 한다.

컨베이어 벨트에 박스 모양 로봇을 하나씩 올리려고 한다. 로봇은 올리는 위치에만 올릴 수 있다. 언제든지 로봇이 내리는 위치에 도달하면 그 즉시 내린다. 로봇은 컨베이어 벨트 위에서 스스로 이동할 수 있다. 로봇을 올리는 위치에 올리거나 로봇이 어떤 칸으로 이동하면 그 칸의 내구도는 즉시 1만큼 감소한다.

컨베이어 벨트를 이용해 로봇들을 건너편으로 옮기려고 한다. 로봇을 옮기는 과정에서는 아래와 같은 일이 순서대로 일어난다.

벨트가 각 칸 위에 있는 로봇과 함께 한 칸 회전한다.
가장 먼저 벨트에 올라간 로봇부터, 벨트가 회전하는 방향으로 한 칸 이동할 수 있다면 이동한다. 만약 이동할 수 없다면 가만히 있는다.
로봇이 이동하기 위해서는 이동하려는 칸에 로봇이 없으며, 그 칸의 내구도가 1 이상 남아 있어야 한다.
올리는 위치에 있는 칸의 내구도가 0이 아니면 올리는 위치에 로봇을 올린다.
내구도가 0인 칸의 개수가 K개 이상이라면 과정을 종료한다. 그렇지 않다면 1번으로 돌아간다.
종료되었을 때 몇 번째 단계가 진행 중이었는지 구해보자. 가장 처음 수행되는 단계는 1번째 단계이다.

입력

첫째 줄에 N, K가 주어진다. 둘째 줄에는 A1, A2, ..., A2N이 주어진다.

출력

몇 번째 단계가 진행 중일때 종료되었는지 출력한다.

제한

2 ≤ N ≤ 100
1 ≤ K ≤ 2N
1 ≤ Ai ≤ 1,000

예제 입력 1

3 2
1 2 1 2 1 2

예제 출력 1

2

예제 입력 2

3 6
10 10 10 10 10 10

예제 출력 2

31

예제 입력 3

4 5
10 1 10 6 3 4 8 2

예제 출력 3

24

예제 입력 4

5 8
100 99 60 80 30 20 10 89 99 100

예제 출력 4

472

알고리즘 분류

• 구현
• 시뮬레이션

코드 - python3 성공

import sys
input = sys.stdin.readline
from collections import deque

n, k = map(int, input().split())
belt = deque(list(map(int, input().split())))
robot = deque([0] * n) # 로봇 위치
res = 0 # 걸린 시간

while 1:
    belt.rotate(1) # 벨트 한칸 회전
    robot.rotate(1) # 로봇 한칸 회전
    robot[-1] = 0  # 로봇이 내려가는 부분이니 0
    if sum(robot):  # 로봇이 존재하면
        for i in range(n - 2, -1, -1):  # 로봇 내려가는 부분 인덱스 i-1 이므로 그 전인 i-2부터 역순
            # 현재 위치에 로봇이 있고, 다음 위치에 로봇 없을 때 다음 벨트의 내구성이 1이상이면
            if robot[i] == 1 and robot[i + 1] == 0 and belt[i + 1] >= 1:
                robot[i + 1] = 1 # 로봇 한칸 이동
                robot[i] = 0 # 현위치 로봇 내림
                belt[i + 1] -= 1 # 다음 위치 내구성 1 감소
        robot[-1] = 0  # 벨트 끝 내려가는 부분은 로봇 내림
    if robot[0] == 0 and belt[0] >= 1: # 첫 위치에 로봇 없고, 내구성 1이상일 때
        robot[0] = 1 # 첫 위치에 로봇 올림
        belt[0] -= 1 # 벨트 내구성 1 감소
    res += 1 # 시간 카운팅
    if belt.count(0) >= k: # 내구성 0인 칸 수가 k 이상일 때
        break

print(res)