[Java] 숫자 데이터의 각종 표현법

서정범·2023년 3월 30일

Java

JAVA

목록 보기

2/6

각종 표현법

우리가 평소에 일상생활에서 사용하는 수학적 데이터를 컴퓨터에서는 어떻게 처리할까요?

기본적으로 컴퓨터에서는 10진법이 아닌 2진법을 사용합니다.

2진법을 만드는 방식을 알고있는데 그렇다면 컴퓨터에서 음수를 이진수로 어떻게 표현 할까요?

그리고 실수의 경우 무한 소수는 어떻게 처리을 할까요? 대소 비교가 가능할까요?

여기서 다뤄볼 것은 공부하다보면 한번씩 맞닥드릴 수 있는 것을 정리할 것입니다.

2진수, 8진수, 16진수 저장법
음수의 2진수 표현, 가산법(2의 보수)
무한 소수(순환 소수, 비순환 소수)

2진수, 8진수, 16진수

컴퓨터는 데이터를 2진수로 저장하기 때문에, 2의 N승인 2, 8, 16은 유의미한 숫자입니다.

따라서, 자바를 통해 10진수(Decimal)외에 16진수(Hexadecimal), 8진수(Octal), 2진수(Binary)를 표현하는 법을 알아보겠습니다.

기본적인 표기법부터 알아본 후 10진수에서 각 진수로 변환하는 법과 그 반대의 경우를 알아보겠습니다.

표기법은 두가지로 알아볼 것입니다.

직접 표기법
내장 함수 사용

일단 직접 표기법을로만 먼저 알아봅시다.

직접 표기법

2진수와 8진수, 16진수를 int형 변수에 그대로 대입하고자 할 때 어떻게 숫자를 넣어주면 될 지 알아보도록 하겠습니다.

코드를 통해서 살펴보겠습니다.

// 2진수를 저장할 때는 정수 앞에 0B 혹은 0b를 붙임
int binary = 0B1010;

// 8진수를 저장할 때는 정수 앞에 0을 붙임
int octa = 064;

// 16진수를 저장할때는 정수 앞에 0X 혹은 0x를 붙임
int hexa = 0X3a4c;

이 방식을 통해서 우리는 직접 각 진수의 데이터를 변수에 저장할 수 있습니다.

그렇다면 변환은 어떻게 해야 할까요?

이때 우리는 Built-In Function(내장 함수)를 사용합니다.

10진수 -> 2진수, 8진수, 16진수 변환

java.lang.Integer의 toBinaryString(), toOctalString(),toHexaString() 메소드를 이용하여 10진수를 2진수, 8진수, 16진수 문자열로 변환할 수 있습니다.

리턴 타입	클래스	메소드	설명
static String	java.lang.Integer	toBinaryString(int i)	10진수 -> 2진수
static String	java.lang.Integer	toOctalString(int i)	10진수 -> 8진수
static String	java.lang.Integer	toHexaString(int i)	10진수 -> 16진수

예제 코드를 통해 살펴봅시다.

public class NumberConvert {
    public static void main(String[] args) {
        int decimal = 10;
 
        String binary = Integer.toBinaryString(decimal); // 10진수 -> 2진수
        String octal = Integer.toOctalString(decimal); // 10진수 -> 8진수
        String hexaDecimal = Integer.toHexString(decimal); // 10진수 -> 16진수
 
        System.out.println("10진수 : " + decimal);	// 출력: 10
        System.out.println("2진수 : " + binary);		// 출력: 1010
        System.out.println("8진수 : " + octal);		// 출력: 12
        System.out.println("16진수 : " + hexaDecimal);// 출력: a
    }
}

2진수, 8진수, 16진수 -> 10진수 변환

java.lang.Integer 클래스의 parseInt()메소드를 이용하여 2진수, 8진수, 16진수 문자열을 10진수 Integer로 변경할 수 있습니다.

리턴 타입	클래스	메소드	설명
static int	java.lang.Integer	parseInt(String s)	문자열(s)을 10진수로 읽어서 int로 반환합니다.
static int	java.lang.Integer	parseInt(String s, int radix)	문자열(s)을 변환할 진수(radix)로 읽어서 int로 반환합니다. (따라서, 2번째 파라미터(radix)를 10으로 입력하면, parseInt(String s)와 같습니다.)

해당 방식도 예제를 통해서 살펴봅시다.

public class NumberConvert {
    public static void main(String[] args) {
 
        int binaryToDecimal = Integer.parseInt("1010", 2);
        int octalToDecimal = Integer.parseInt("12", 8);
        int hexaToDecimal = Integer.parseInt("A", 16);
 
        System.out.println("2진수(1010) -> 10진수 : " + binaryToDecimal); // 10
        System.out.println("8진수(12) -> 10진수 : " + octalToDecimal); // 10
        System.out.println("16진수(a) -> 10진수 : " + hexaToDecimal); // 10
 
    }
}

음수의 2진수 표현, 가산법

먼저, 음수의 2진수 표현법을 알아보기 이전에 컴퓨터에서 2진수를 어떻게 다루는지부터 알아보고 시작을 합시다.

먼저 컴퓨터는 2진수, 비트 단위가 최소단위로 값을 표현할 수 있는데 n 비트라고 하면 표현할 수 있는 값의 개수는 $2^n$ 개 입니다.

만약, 4비트의 2진수로 양수와 음수를 모두 표현한다고 하면 어떻게 할까요?

1. 절반씩 양수와 음수로 사용하여 순서대로 증가(부호 절대값 방식)

#	2진수	부호있는 10진수
1	0000	0
2	0001	1
3	0010	2
4	0011	3
5	0100	4
6	0101	5
7	0110	6
8	0111	7
9	1000	-0
10	1001	-1
11	1010	-2
12	1011	-3
13	1100	-4
14	1101	-5
15	1110	-6
16	1111	-7

음수를 이렇게 배치하게 되면, 첫번째 비트만 1로 바꾸면 음수가 된다는 장점이 있습니다.

하지만, 두 수를 더했을 때 2진수로 0이 되지 않는다는 것과 0이 두 개 존재한다는 단점이 있습니다.

예를 들어, 5(0101) + -5(1101) = 0(0000)이 되어야 하지만, 10010이 되어 맨 앞자리가 떨어져 나간다고 해도 0010이 되버립니다.

2. 2의 보수법

#	2진수	부호있는 10진수
1	0000	0
2	0001	1
3	0010	2
4	0011	3
5	0100	4
6	0101	5
7	0110	6
8	0111	7
9	1000	-8
10	1001	-7
11	1010	-6
12	1011	-5
13	1100	-4
14	1101	-3
15	1110	-2
16	1111	-1

'2의 보수법'에 의해 음수를 배치하면, 절대값이 같은 양수와 음수를 더했을 때 2진수로 0의 결과를 얻을 수 있습니다.

⚡ 1의 보수와 2의 보수 ⚡

보수란, 두 수의 합이 진법의 밑수(N)가 되게 하는 수를 말합니다. 예를 들어서, 10진수 4의 10의 보수는 6이고, 10진수 2의 10의 보수는 8입니다. 보수는 컴퓨터에서 음의 정수를 표현하기 위해 고안되었습니다. 컴퓨터 내부에서는 사칙 연산을 할 때 덧셈을 담당하는 가산기(Adder)만 이용하기 때문에 뺄셈은 덧셈으로 형식을 변환하여 계산해야 합니다. 즉, 컴퓨터 내부에서는 A - B를 계산할 때 B의 보수(-B)를 구한 다음 A + (-B)로 계산하는 것입니다.

👉 1의 보수: 각 자릿수의 값이 모두 1인 수에서 주어진 2진수를 빼면 1의 보수를 얻을 수 있습니다.
예시) 2진수 1010의 1의 보수는 0101입니다.
👉 2의 보수: 1의 보수에 1을 더한 값과 같습니다.
예시) 2진수 1010에 대한 2의 보수를 구하려면 2진수 1010에 대한 1의 보수 0101을 구한 다음 1을 더해 0110을 얻습니다.

왜 2의 보수를 사용하는 것일까?

만약, 1의 보수를 사용해서 5와 -5를 더해본다고 생각해봅시다.

5(0101) + -5(1010) = 0(1111) 이와 같이 나옵니다. 애석하게도 우리가 원하던 표현인 0000이 나오는 것이 아닌 1111이 나왔습니다. 따라서, 2의 보수를 사용하는 것입니다.

2의 보수를 사용해서 더하면 다음과 같이 됩니다.

5(01010) + -5(1011) = 0(10000 => 0000) (

현재 4비트 컴퓨터로 가정하고 있는데 4비트 컴퓨터의 경우 4비트 까지만 표기가 가능하므로 4비트를 넘어가는 숫자는 지워집니다. 그래서 0000만 남는 것입니다.

Reference

2진수 실수 표현

앞서 제시했던 2진수의 무한소수 표기 문제에 대해서 처리하기 전에 먼저, 실수를 2진수로 어떻게 표현하는가에 대해서 알아보고 넘어가도록 하겠습니다.

위에서 봤듯이 정수 부분에서 2진수를 표기하기 위해선 2로 나눠가면서 나머지를 가지고 하나하나 앞에다가 붙여가면서 처리했습니다.

예를 들어, 27의 경우 다음과 같습니다.

27 / 2 = 13 + 1 => [1]
13 / 2 = 6 + 1 => [11]
6 / 2 = 3 + 0 => [011]
3 / 2 = 1 + 1 => [1011]
1 / 2 = 0 + 1 => [11011]

이와 같은 순서로 처리를 했습니다.

실수의 경우는 이와 반대로 2를 곱해가면서 처리를 하는데 2를 곱하고 나서 정수 부분을 뽑아내면서 나머지 소수 부분에 계속해서 2를 곱해가며 1을 만들면 종료하는 방식을 사용합니다.

예를 들어서 0.625를 2진수 표기법으로 표현해 보겠습니다.

0.625 * 2 = 1.25 => [0.1]
1.25 * 2 = 0.5 => [0.10]
0.5 * 2 = 1 => [0.101]

2진수 무한소수

지금까지 앞서 컴퓨터가 데이터를 받아서 2진수로 저장하는 방식을 살펴보았습니다.

근데, 우리는 10진수에서 2진수로 바꿀 때 딱 나누어 떨어지는 경우도 있지만, 안 나누어 떨어지는 경우도 많다는 것을 알고있습니다.

예를 들어서 0.1을 2진수로 표현한다면 값이 나누어 떨어지지 않고 0.0001100110011... 로 무한으로 반복되는 현상이 나타납니다.

이를 무한 소수라고 합니다.

이처럼 10진수 세계에서 2진수의 세계로 소수점을 변환하는 것은 높은 확률로 정확한 변환이 불가능 합니다.

👉 소수의 끝이 5가 아닌 수를 2진수로 소수를 표현할 경우 무한 소수가 발생한다고 보면 됩니다.

이것을 정확히 이해하기 위해 실수의 메모리 표현을 알아봐야 합니다.

실수의 메모리 표현

컴퓨터의 메모리는 2진수 체계를 기반으로 데이터를 저장합니다.

당연히 실수도 2진수로 메모리 비트로 표현해야 하며 정수에 비해서 상대적으로 복잡한 편이다.

컴퓨터에서는 실수를 표현하는 방식으로는 대표적으로 고정 소수점 방식(Fixed-Point Number Representation)과 부동 소수점 방식(Floating-Point Number Representaion)으로 나눌 수 있습니다.

고정 소수점 방식

고정 소수점 방식은 메모리를 정수부와 소수부로 고정으로 나누고 지정하여 처리하는 방식입니다.

소수부의 자릿수를 미리 정하고 고정된 자릿수의 소수를 표현하기 때문에 직관적입니다.

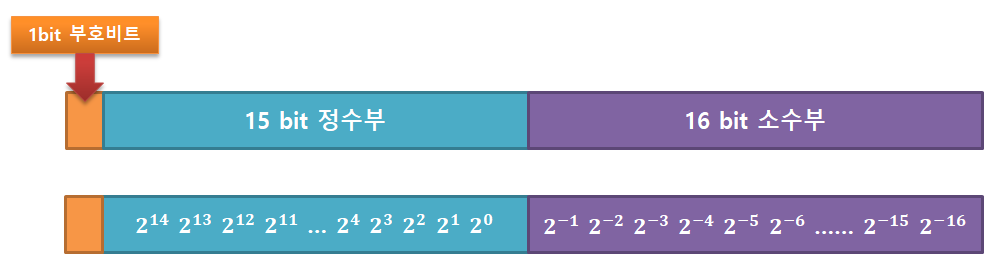
👉 맨 좌측의 1bit 부호 비트란 양수/음수를 표현하기 위한 비트입니다. 0이면 양수, 1이면 음수를 통칭합니다.

예를 들어서 5.625 숫자를 이진수로 변환하고 컴퓨터 메모리에 고정 소수점 방식으로 표현한다면 다음과 같이 됩니다.

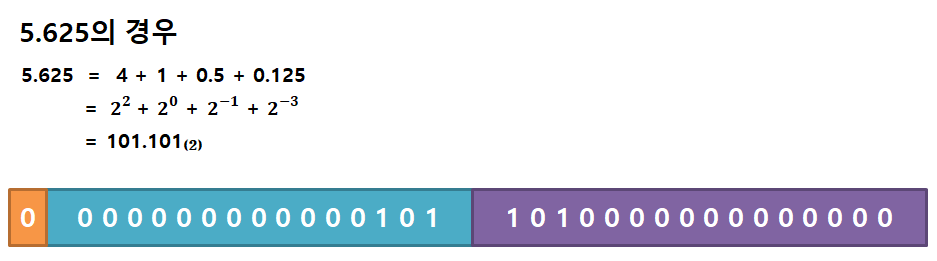
즉, 위에서 살펴보았던 이진수 실수 계산법을 그대로 적용하고 결과값을 각각 정수부, 소수부 메모리 비트에 넣어주면 실수 표현이 완료되는 것입니다.

이처럼 직관적으로 메모리에 실수 표현을 할 수 있다는 장점이 있지만, 표현 가능한 범위가 매우 적다는 치명적인 단점이 있습니다.

Java의 float 타입을 기준으로 실수 메모리는 총 32비트를 할당받게 되는데, 고정 소수점 방식으로 메모리를 반띵하여 설계하였다면, 다음과 같이 정수부 비트에서 최대로 표현할 수 있는 숫자는 $2^{15} - 1$ 인 $32767$ 이 되게 된다.

즉, 40000.01 이라는 실수가 있다면 표현 범위를 넘어 메모리에 적재할 수 없게 되는 것입니다.

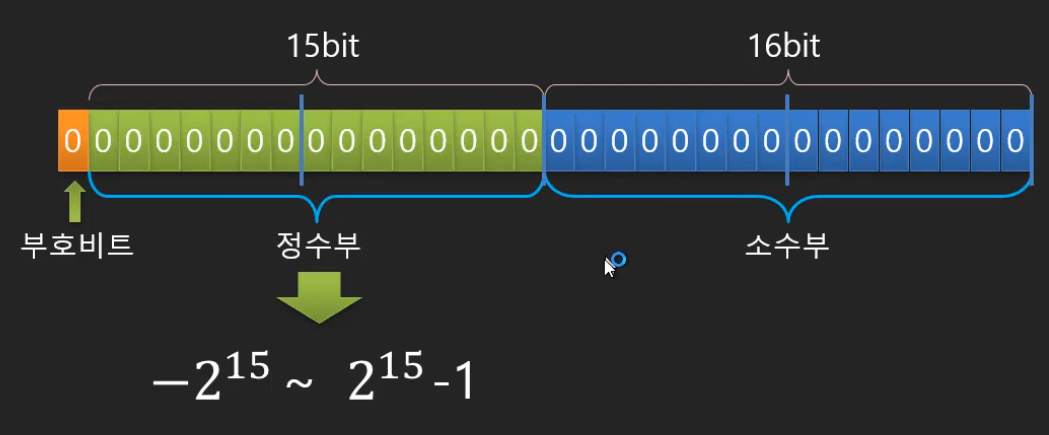
이 밖에도 낭비되는 공간이 많이 생긴다는 단점도 존재합니다.

22777.12라는 실수가 있을 경우, 고작 0.12라는 작은 숫자를 표현하기 위해 16비트의 소수부를 모두 사용한다는 것은 아무리 봐도 설계 미스라고 밖에 보이지 않는다.

이러한 공간 낭비를 줄이고 효율적으로 실수 메모리를 표현하기 위해 컴퓨터는 부동 소수점 방식을 사용합니다.

부동 소수점 방식

부동 소수점 방식(floating point)은 둥둥 떠다닌다 (floating) 라는 의미로, 표현할 수 있는 값을 범위를 최대한 넓혀 오차를 줄이자는 시도에서 나온 방식입니다.

부동 소수점은 고정 소수점 방식과는 달리 메모리를 가수부(23bit)와 지수부(8bit)로 나눕니다.

기수부에는 실제 실수 데이터 비드들이 들어가고, 지수부에는 소수점의 위치를 가르키는 제곱승이 들어간다고 보면 됩니다.

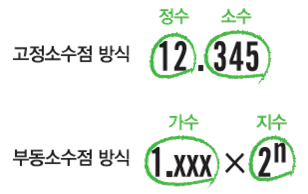
뭔가 직관적이지 않아 오히려 번거롭게 보일수도 있겠지만, 이런식으로 실수를 표현하는 이유는 큰 범위의 값을 표현하기 위해서입니다.

위의 고정 소수점 방식에는 따로 물리적으로 정수부와 소수부로 나누어 각각 15bit, 16bit밖에 사용하지 못하였지만, 부동 소수점 방식은 실수의 값 자체를 가수부(23bit)에 넣어 표현하기 때문에 보다 큰 비트의 범위를 가지게 되며, 정수부가 크든 소수부가 크든 상관없이 가수부 내에서 전체 실수를 표현하기 때문에 공간 낭비 문제도 해결되는 것이다.

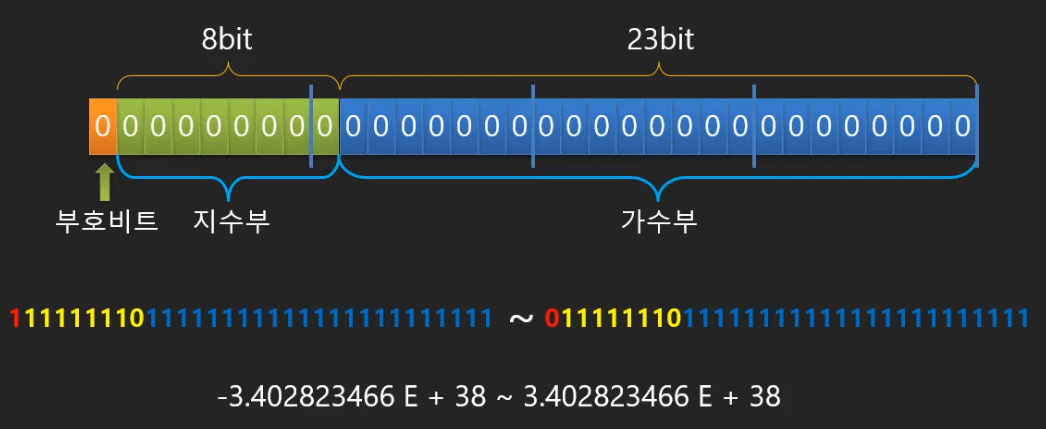
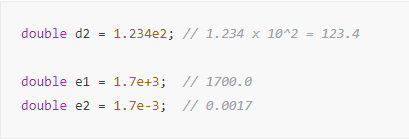
⚡ 지수(e) 표기법 ⚡

지수 표기법은 아주 큰 숫자나 아주 작은 숫자를 간단하게 표기할 때 사용되는 표기법으로, 과학적 표기법(scientific notation)이라고도 불립니다.

길다란 실수 숫자를 나타내는 데 필요한 자릿수를 줄여 표현해준다는 장점이 있습니다.

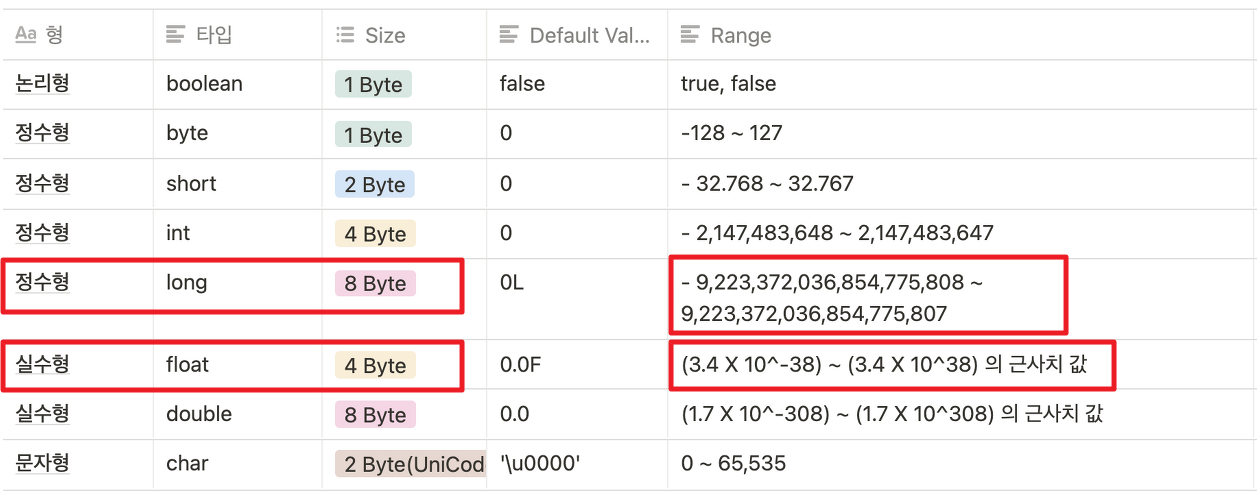
큰 범위의 값이라고 해서 얼마나 큰 범위냐 하면은, 실제로 자바의 타입 범위들을 보면 8바이트를 사용하는 정수형 long타입 수 범위보다, 4바이트를 사용하는 실수형 float 타입 수 범위가 훨씬 더 크다는 것을 볼 수 있습니다.

부동 소수점 계산 방법

현재 사용되고 있는 부동 소수점 방식은 대부분 IEEE 754 표준을 따르고 있습니다. 그리고 자바도 이 표준을 따르고 있습니다.

IEEE 754 표준의 부동 소수점 수학적 수식은 다음과 같이 된다.

±(1.M) × 2＾E-127 

±(1.가수부) × 2^지수부-127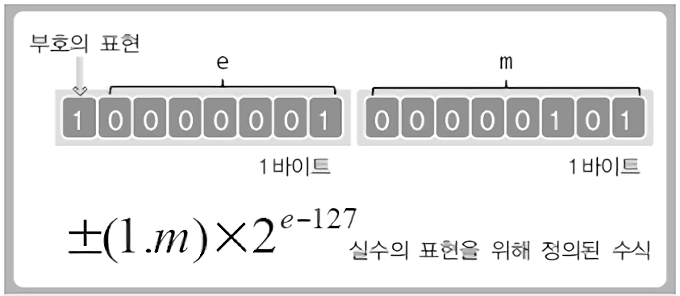

기호	의미	설명
S	부호(Sign bit)	0이면 양수, 1이면 음수
E	지수부(Exponent)	부호있는 정수. 지수의 범위는 －127 ~ 128(float), －1023 ~ 1024(double)
M	가수부(Mantissa)	실제값을 저장하는 부분. 10진수로 7자리(float), 15자리(double)의 정밀도로 저장 가능

이것만 보고는 이해하기 어렵다. 예시를 통해 살펴보도록 하겠습니다.

-118.625라는 실수를 부동 소수점으로 변환하는 예를 직접 행해봅시다.

1. 음수이기에 최상위 비트를 1로 설정해줍니다.

2. 절대값 118.625를 이진법으로 변환해줍니다.

# 정수부 변환
118
= 1110110(2)

# 소수부 변환
0.625
= 0.625 x 2 = 1.250 → 정수부 1
= 0.250 x 2 = 0.500 → 정수부 0
= 0.500 x 2 = 1.000 → 정수부 1
= 101(2)

# 결과
118.625 
= 1110110.101(2)

3. 소수점을 이동시켜 정수부가 한다리로 되도록 변환해줍니다. (그러면 지수 6이 만들어집니다.)

1110110.101 → 1.110110101 x 2^6

✅ Tip

소수점을 이동시키는 것을 정규화(Normalization)이라고 부릅니다.
정규화라는 단어는 수학이나 컴퓨터 분야에서 다양한 의미로 쓰이지만 여기서 말하는 정규화라는 것은 2진수를 1.xxxx... * 2^n 꼴로 변환하는 것을 말한다고 보면 됩니다.

4. 가수부 비트에 실수값 그대로를 넣는다(점 무시)

5. 지수에 바이어스 값(127)을 더하고 지수부 비트에 넣는다.

6 + 127 
= 133
= 100000101(2)

✅ Info

32bit IEEE 754 형식에는 bias라는 고정값(127)이 존재합니다.

이 ibas라는 값을 왜 쓰냐면, 지수가 음수가 될 수도 있는 케이스가 있기 때문입니다. $(2^{10}$ or $2^{-10})$

예를 들면 0.000101(2)이라는 이진수가 있다고 가정해 봅시다.

이를 1.xxx... 2^n 형식으로 표현하기 위해선, 오른쪽 소수점을 밀면 1.01 2^ -4가 됩니다.

이 -4가 음수 지수를 8자리 비트로 표현하기 위해, (10진수 기준으로) 0 ~ 127 구간은 음수, 128 ~ 255 구간은 양수를 표현하도록 만든 것입니다.

그래서 게산된 지수에 127 bias 값을 더하여, 127보다 작으면 음수, 127보다 크면 양수로 구분할 수 있는 것입니다.

배정도 부동 소수점 방식

자바에서는 float(32bit)와 double(64bit) 자료형이 있는 것처럼,

부동 소수점 방식에도, 지금까지 위에서 살펴본 32비트 체계를 32비트 단정도 (Single-Precision), 64비트 체계를 64비트 배정도 (Double-Precision)이라고 부릅니다.

double형 64비트 체계에서는 지수부가 11비트, 가수부가 52비트 입니다.

지수부가 2^11 즉, 2048개의 수를 표현할 수 있으므로 0 ~ 1023 구간은 음수, 1024 ~ 2047 구간은 양수 지수를 의미하며, 이때 bias 고정값은 1023이 된다는 차이점이 존재합니다.

프로그래밍에서의 소수 계산 오차

이제까지 컴퓨터에서 실수를 저장하는 방식은 고정 소수점 방식과 부동 소수점 방식을 알아보았고, 좀 더 큰수를 표현하여 저장할 수 있는 부동 소수점 방식을 사용하는 이유를 알아 보았습니다.

하지만, 아직 처음부터 궁금했던 무한 소수 처리는 나오지 않았다.

부동 소수점 방식으로도 무한 소수 처리가 불가능 하기 때문에 결국 메모리 한계까지 소수점을 집어넣고 어느 부분에서 끊어 반올림을 해주어야 합니다.

즉, 컴퓨터의 메모리는 한정적이기 때문에 실수의 소숫점을 표현할 수 있는 수의 제한이 존재하게 될 수 밖에 없습니다.

그리고 실수를 표현하는 숫자 제한이 있다는 것은 곧 부정확한 실수의 계산값을 초래한다는 뜻이기도 합니다.

이것은 자바뿐만 아니라, 모든 프로그래밍 언어에서 발생하는 기본적인 문제입니다.

다음 예제를 수행해보면 컴퓨터의 실수 연산 초차를 발견할 수 있습니다.

double value1 = 12.23;
double value2 = 34.45;

// 기대값 : 46.68
System.out.println(value1 + value2); // 46.68000000000001

12.23와 34.45을 더했으니 기대 결과로 46.68이 나와야 되지만, 실제로는 46.68000000000001가 출력되어 버립니다.

이는, 10진수 소수의 값인 12.23과 34.45을 2진수로 변환하는 과정에서 소수점이 안떨어지는 무한 소수 현상이 나타나 메모리 할당 크기의 한계 때문에 어느 자리수 까지의 반올림 표현밖에 못하고, 그런 부정확한 값을 이용해 연산을 하였으니 당연히 결과값도 부정확하게 나오게 된 것입니다.

물론 수 자체의 크기로서는 근사한 차이 정도 밖에 안되겠지만, 금융이나 드론과 같은 관련 프로그램에서는 이 오차가 큰 영향을 미칠 수 있기 때문에 아주 정확한 계산이 필요합니다.

따라서 이러한 컴퓨터의 실수 연산 문제를 해결 하기 위해 자바(Java)에서는 두가지 방법을 제공합니다.

int, long 정수형 타입으로 형변환
BigDecimal 클래스 이용

소수 정확하게 계산하는 방법

정수 치환하여 계산

예를 들어 25.35에서 100을 곱해서 2535로 정수로 치환해서 계산하고 다시 100을 나누어서 소수 결과값을 도출하는 일종의 꼼수 방법이라고 보면 됩니다.

double a = 1000.0;
double b = 999.9;
System.out.println(a - b); // 0.10000000000002274


// 각 숫자에 10을 곱해서 소수부를 없애주고 정수로 형변환
long a2 = (int)(a * 10);
long b2 = (int)(b * 10);
double result = (a2 - b2) / 10.0; // 그리고 정수끼리 연산을 해주고, 다시 10.0을 나누기 하여 실수로 변환하여 저장
System.out.println(result); // 0.1

BigDecimal 클래스

다만 소수의 크기가 9자리를 넘지 않으면 int 타입을 사용하면 되고, 18자리를 넘지 않으면 long 타입을 사용하면 되지만, 컴퓨터에서는 데이터의 표현 범위가 제한되어 있기 때문에, 만일 18자리를 초과하면 BigDecimal 클래스를 사용해야 합니다.

// BigDecimal 자료형을 사용
BigDecimal bigNumber1 = new BigDecimal("1000.0");
BigDecimal bigNumber2 = new BigDecimal("999.9");
BigDecimal result2 = bigNumber1.subtract(bigNumber2); // bigNumber1 - bigNumber2
System.out.println(result2); // 0.1

✅ Tip

BigDecimal를 사용할 경우 기본형 타입보다 사용하기 불편하고 실행 속도가 느려진다는 단점이 있습니다. 하지만 소수를 계산함에 있어서 필수로 자주 이용되는 클래스이니 반드시 익히기를 권합니다.

double과 float의 비교연산 문제

실수를 더하거나 뺴는 계산에 대한 오차는 해결했지만 한 가지 더 문제점이 존재합니다.

자바의 float는 4바이트 실수, double은 8바이트 실수 값을 저장 할 수 있는데, 문제는 컴퓨터는 부동 소수점으로 실수를 표현하기 때문에 double은 float 간의 정밀도(정확도) 차이가 발생한다는 점이다.

System.out.println(1.0 == 1.0f);  // 결과 : true
System.out.println(1.1 == 1.1f);  // 결과 : false
System.out.println(0.1 == 0.1f);  // 결과 : false
System.out.println(0.9 == 0.9f);  // 결과 : false
System.out.println(0.01 == 0.01f);  // 결과 : false

위 코드를 보면 다 true일 것 같지만, 맨 윗줄만 제외하고 모두 false를 출력합니다.

눈에 보이지는 않지만 바로 float와 double 자료형의 실수 표현의 정밀도의 차이가 발생하기 때문입니다.

따라서 double과 float값을 비교할 때에는 모두 float로 형변환 하거나 정수로 변환하여 비교해야 한다.

System.out.println((float)1.1 == 1.1f);  // 결과 : true
System.out.println(0.1f == (double)0.1f);  // 결과 : true

System.out.println(0.1 == (double)0.1f);  // 결과 : false