문제
삼각형의 크기 n(1 ≤ n ≤ 500)이 주어지고, 둘째 줄부터 n + 1번째 줄까지 다음과 같은 정수 삼각형이 주어진다.
현재 위치에서 대각선 왼쪽 또는 대각선 오른쪽 값 중 하나를 선택해서 누적으로 더하며 맨 위층부터 한 층씩 내려올 때, 그 합이 최대가 되는 경로의 합을 출력하는 문제이다.
풀이
한 층 아래로 내려오는 2가지 경우가 존재하는데, 숫자 총합이 최대가 되는 경로를 찾기 위해서는 제일 윗층 숫자에서 제일 아랫층 각 숫자로 도달하는 각 경로의 최대 총합을 알아야 한다.
그래서 DP로 접근을 했고, 점화식은 아래와 같이 그림을 그려 구할 수 있었다.
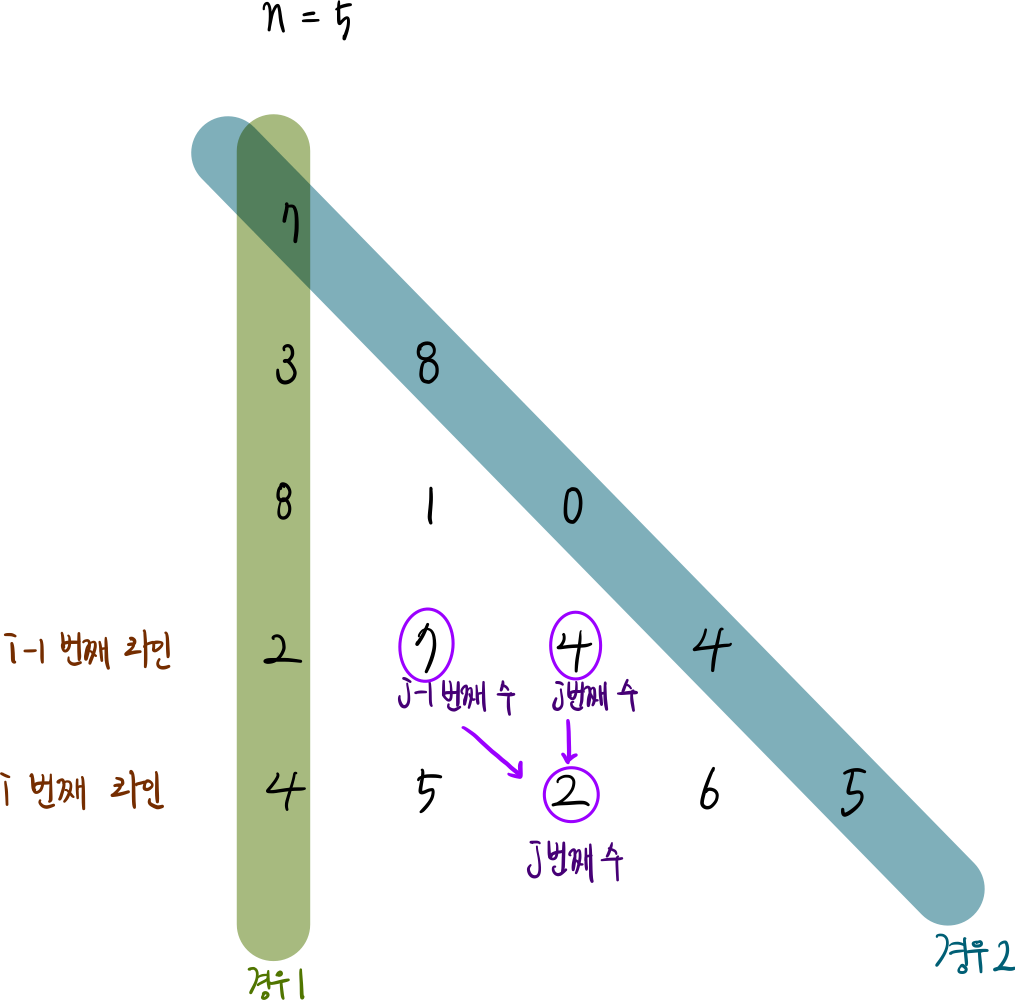
자세하게 설명을 하면..
i번째 라인의 j번째 수에 도달하는 경로에서 최대 총합은, 아래의 2가지 경우만 존재한다.
[1] i - 1번째 라인의 j - 1번째 수에서 오는 경우
[2] i - 1번째 라인의 j번째 수에서 오는 경우
그래서 DP[i][j]를 i번째 라인의 j번째 수에 도달하는 경로 중 만들어지는 최대 총합이라 정의하면, 점화식은 다음과 같다.
DP[i][j] = DP[i][j] + max(DP[i - 1][j - 1], DP[i - 1][j])
그런데 초록색과 파란색으로 표시된 2개의 경로는 따로 분기 처리를 해줘야 한다.
직접 계산해 보면 알 수 있는데, 두 경로에서 i번째 라인의 j번째 수에 도달하는 경로는 한 가지 경우만 존재한다.
그래서 위의 점화식을 사용할 경우 IndexError(list index out of range)가 발생한다.
따라서 초록색 경로는 윗층에서 그대로 내려오는 것만 가능하므로, DP[i][j] += DP[i - 1][j]로 처리를 해줘야 한다.
그리고 파란색 경로는 윗층 왼쪽에서 내려오는 것만 가능하므로, DP[i][j] += DP[i - 1][j - 1]로 처리를 해줬다.
마지막 i번째 라인에 모든 경로의 최대 총합이 저장되어 있으므로, 이 중 최댓값이 정답이 된다.
아래 코드에서는 따로 DP라는 리스트를 선언하지 않고, 숫자를 입력 받은 triangle이라는 2차원 리스트를 그대로 사용했다.
어차피 구하는 것이 누적 합이기 때문이다.
코드(정답)
import sys
# 입력
n = int(sys.stdin.readline())
triangle = []
for _ in range(n):
triangle.append(list(map(int, sys.stdin.readline().split())))
# DP
for i in range(1, n):
for j in range(i + 1):
# 1. 가장 왼쪽 라인인 경우: 바로 위에 있는 값을 더한다.
if j == 0:
triangle[i][j] += triangle[i - 1][j]
# 2. 가장 오른쪽 라인인 경우: 바로 위 왼쪽에 있는 값을 더한다.
elif i == j:
triangle[i][j] += triangle[i - 1][j - 1]
# 3. 1과 2 사이 라인인 경우: 바로 위, 바로 위 왼쪽 중 큰 값을 더한다.
else:
triangle[i][j] = triangle[i][j] + max(triangle[i - 1][j - 1], triangle[i - 1][j])
# 출력
print(max(triangle[n - 1]))