백준 창고 다각형 문제 풀이이다.
n개의 직사각형 기둥(폭은 모두 1m)으로 구성된 창고의 지붕을 만들 때, 옆에서 바라본 창고 다각형의 면적의 최솟값을 구하는 문제이다.
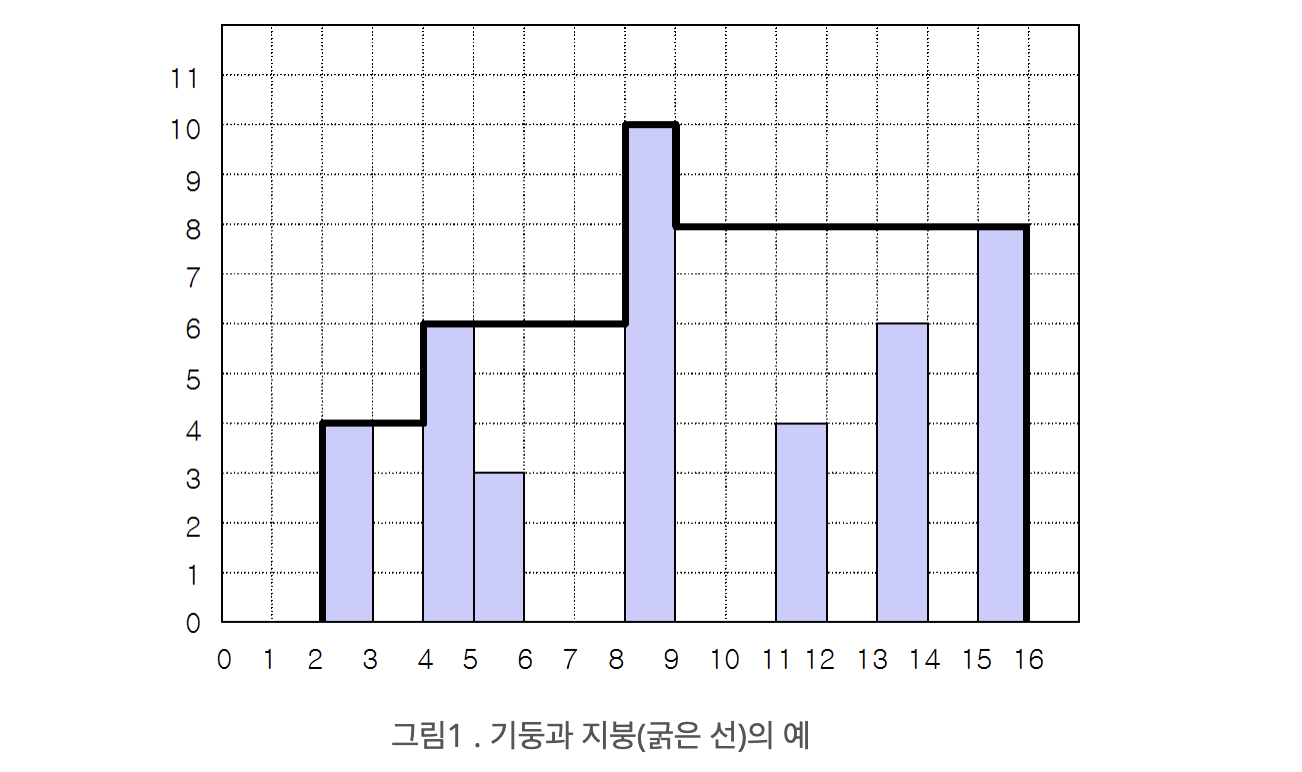
지붕을 만드는 5가지 조건은 다음과 같다.
[1] 지붕은 수평 부분과 수직 부분으로 구성되며, 모두 연결되어야 한다.
[2] 지붕의 수평 부분은 반드시 어떤 기둥의 윗면과 닿아야 한다.
[3] 지붕의 수직 부분은 반드시 어떤 기둥의 옆면과 닿아야 한다.
[4] 지붕의 가장자리는 땅에 닿아야 한다.
[5] 비가 올 때 물이 고이지 않도록 지붕의 어떤 부분도 오목하게 들어간 부분이 없어야 한다.
가장 왼쪽 기둥(l), 가장 오른쪽 기둥(r), 그리고 그 사이에 있는 기둥 중 가장 큰 기둥(m)의 기준점이 된다.
그리고 5번 조건을 만족하기 위해서는 l에서 m까지 계단식으로 올라가야 하고, r에서 m까지 계단식으로 올라가야 한다.
그래서 창고 다각형 면적의 최솟값을 3가지 영역으로 구분했다.
[1] 가장 왼쪽 기둥부터 가장 큰 기둥 직전까지의 면적
[2] 가장 큰 기둥이 차지하는 면적
[3] 가장 오른쪽 기둥부터 가장 큰 기둥 직전까지의 면적
면적을 더할 때는 모든 기둥의 폭이 1m임을 이용했는데, 이는 다르게 말하면 결국 기둥의 높이가 그 기둥이 차지하는 면적이 되는 셈이다.
기둥의 개수가 1,000개 이하이고, 1번째 기둥이 1번 인덱스에 위치한다는 사실을 통해 각 기둥의 높이 정보를 저장하는 리스트 pillars를 선언했다.
pillars[0]는 쓰이지 않으며, pillars[i]는 i번째 기둥의 높이를 의미한다.
'[1] 가장 왼쪽 기둥부터 가장 큰 기둥 직전까지의 면적'을 구하는 과정은 다음과 같다.
왼쪽부터 가장 큰 기둥까지 계단식으로 올라가야 하므로, 탐색 시점에서 기준 높이가 되는 값을 ref_height로 뒀다.
만약 이 값보다 더 큰 값이 나오면 그건 더 높은 계단으로 올라가는 셈이므로 ref_height를 업데이트주고, 그렇지 않다면 현재 ref_height 값이 해당 부분의 면적이므로 area라는 변수에 더해줬다.
'[2] 가장 큰 기둥이 차지하는 면적'은 그냥 가장 큰 기둥의 높이인 max_height를 더해주면 된다.
'[3] 가장 오른쪽 기둥부터 가장 큰 기둥 직전까지의 면적'은 [1]과 똑같은 논리인데, 가장 오른쪽에서부터 가장 큰 기둥까지 계단식으로 올라가야 하므로 인덱스의 역순으로 탐색을 해야 한다.
코드(정답)는 다음과 같다.
# 창고 다각형(https://www.acmicpc.net/problem/2304)
import sys
n = int(sys.stdin.readline())
# 기둥 정보 저장
pillars = [0 for _ in range(1001)]
for _ in range(n):
position, height = map(int, sys.stdin.readline().split())
pillars[position] = height
# 가장 큰 기둥의 길이와 위치 저장
# 만약 가장 큰 기둥이 여러 개라면 가장 왼쪽에 위치한 기둥의 위치를 ref_idx에 저장
max_height = max(pillars)
ref_idx = pillars.index(max_height)
# 조건을 만족하는 창고 다각형의 최소 면적 구하기
area = 0
# (1) ref_idx 기준 왼쪽 영역 탐색
ref_height = -1
for i in range(1, ref_idx):
if pillars[i] > ref_height:
ref_height = pillars[i]
area += ref_height
# (2) ref_idx 영역
area += max_height
# (3) ref_idx 기준 오른쪽 영역 역순 탐색
ref_height = -1
for i in range(1000, ref_idx, -1):
if pillars[i] > ref_height:
ref_height = pillars[i]
area += ref_height
print(area)