Denoising Diffusion Probabilistic Models(DDPM)
-
Jonathan Ho, Ajay Jain, Pieter Abbeel
-
NeurIPS
-
2020
1. Introduction
최근 눈에 띄는 Difusion Model 활용
1) Text-to-Image Genaration
- DALLE2 등
2) 이미지, 오디오 등 다양한 벤치마크 데이터에 상위권 성능 도달What is 'Diffusion'?
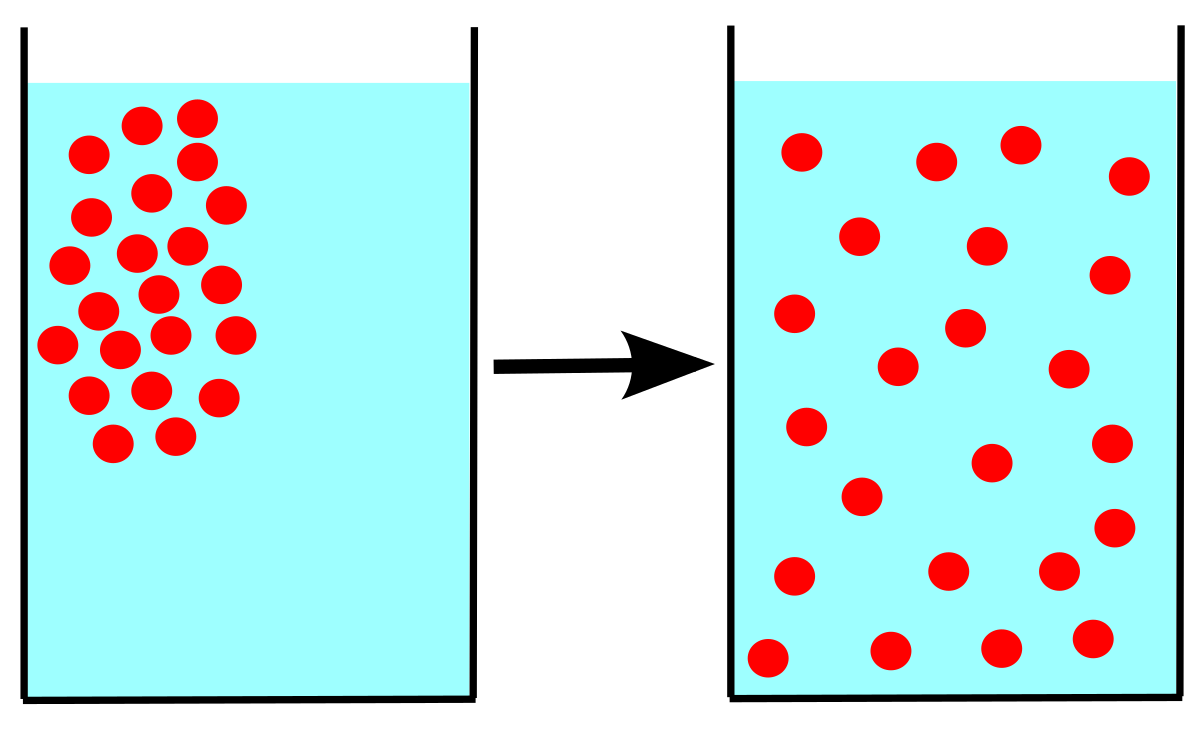
1) 물리 통계 동역학에서 특정한 물질(액, 기체)이 조금씩 번지며 같은 농도로 바뀌는 현상
2) 물질들의 특정한 분포가 서서히 와해되는 과정
3) 2015년 비지도 학습을 위해 처음으로 활용되기 시작함
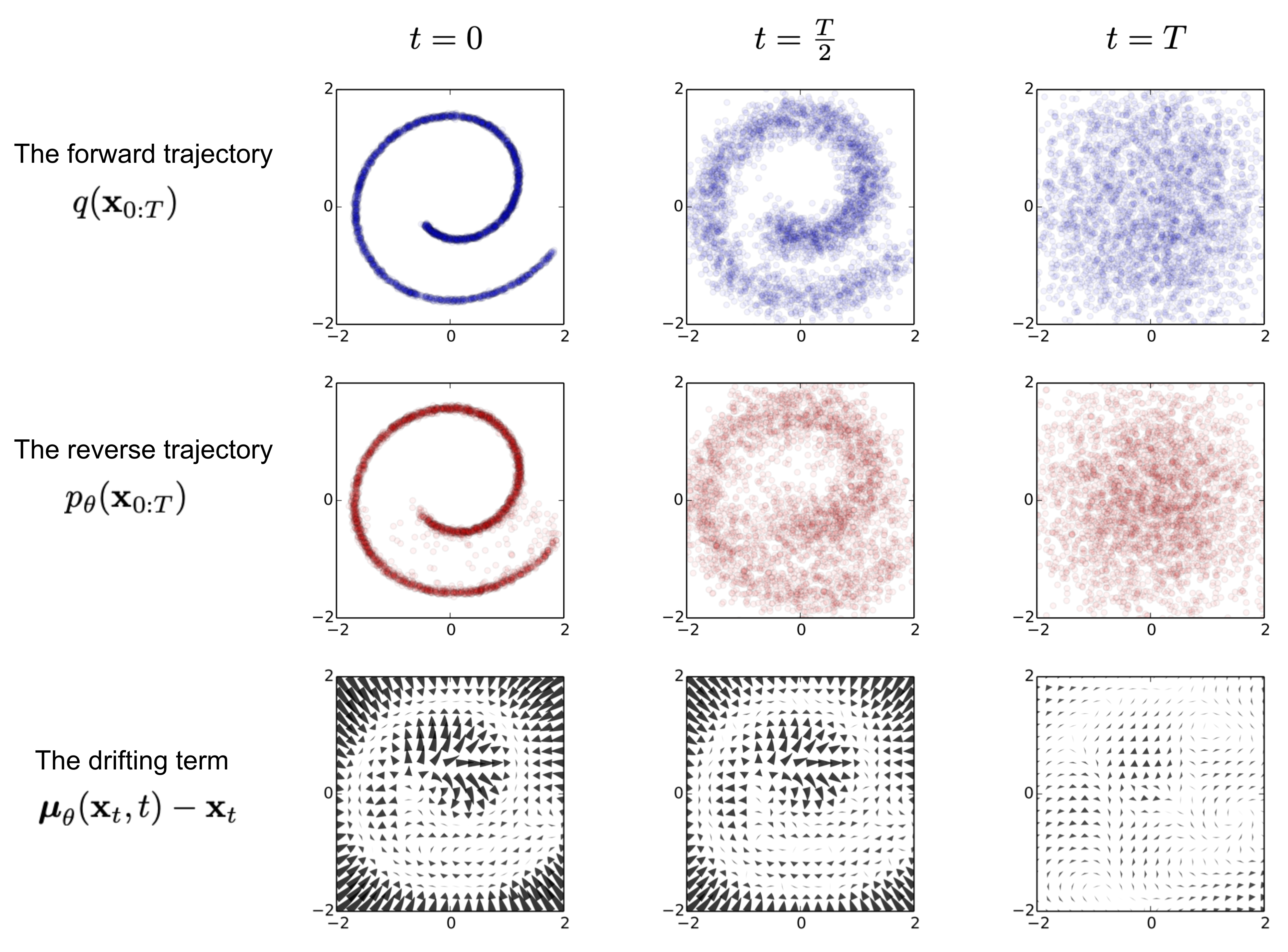
4) 즉, Diffusion = 확산,
특정 데이터 패턴이 서서히 반복적으로 와해되는 과정, Explicit Pattern 에서 Gaussian Noise 가 되는 과정을 "Diffusion Process"라고 설명
5) 대표적인 비지도 학습 방법론인 이미지 생성 Task에서 높은 성능을 보이며 주목을 받음Prerequisite
Markov Chain
-
정의 : Markov 성질 을 갖는 이산 확률과정
-
Markov 성질 : 특정 상태의 확률(t+1)은 오직 현재(t)의 상태에 의존한다
-
이산 확률과정 : 이산적인 시간(0초, 1초, 2초, ..) 속에서의 확률적 현상
-
예) 내일의 날씨는 오늘의 날씨만 보고 알 수 있다.(내일 날씨의 조건은 오로지 오늘의 날씨!
Normalizing Flow
-
DDPM과 직접적 연관은 없으나 다른 생성 모델과 비교하기 위해 필요함
-
심층 신경망 기반 확률적 생성 모형 중 하나
-
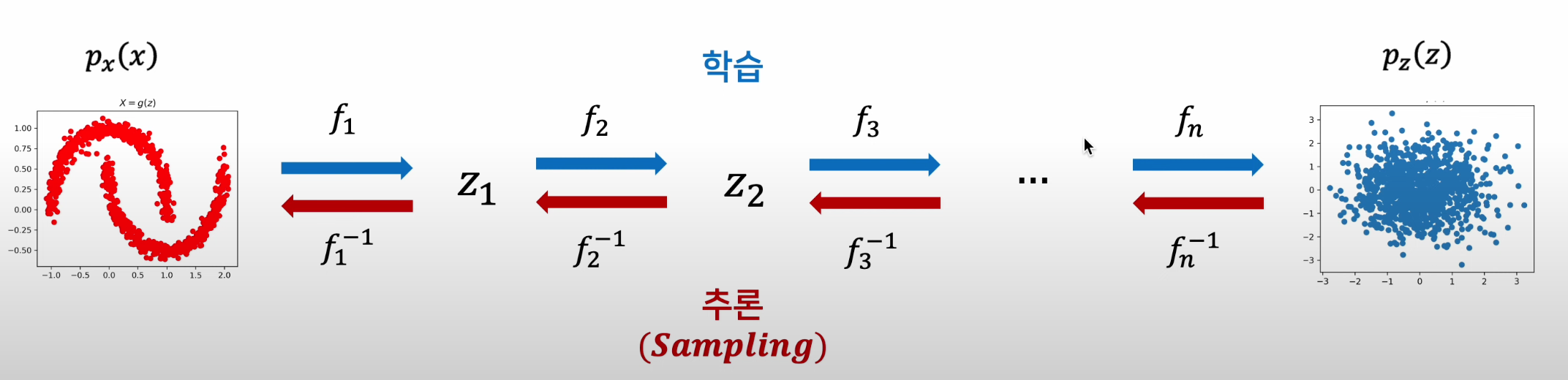
잠재 변수(z)기반 확률적 생성모형으로서, 잠재 변수(z) 획득에 "변수 변환" 공식을 활용
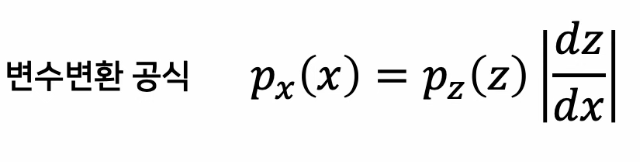
Overview of Generation Models
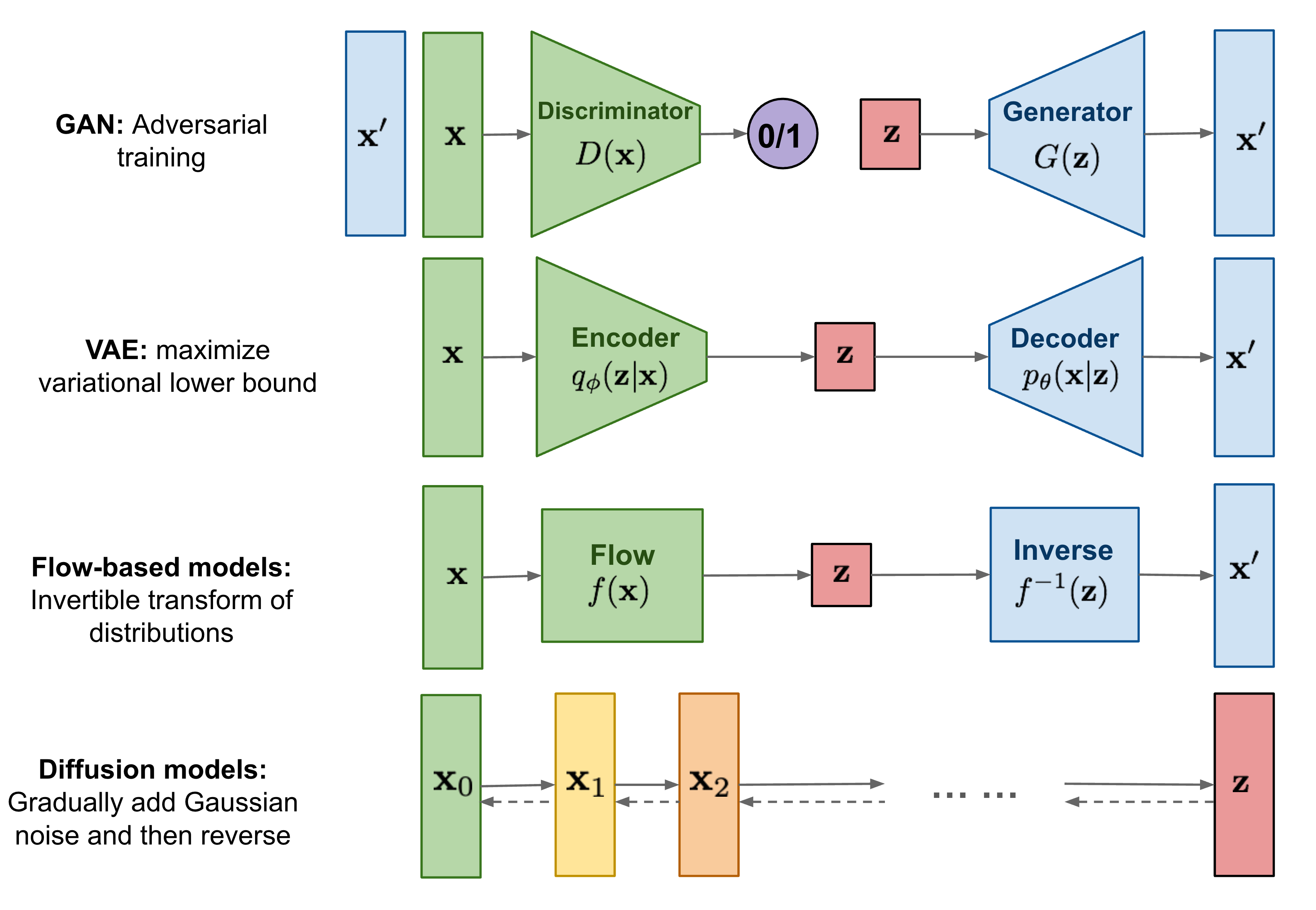
이미지 출처 : Waht are diffusion models
-
반복적인 변화(iterative transformation)를 활용한다는 점에서 Flow-based Models 와 유사
-
분포에 대한 변분적 추론을 통한 학습을 진행한다는 점은 VAE와 유사
-
최근에는 Diffusion Model의 학습에 Adversarial Training을 활용하기도 함(Diffusion GAN, 2022)
2. Generative Model Overview
Probabilistic Generative Model : Latent Variable Model
Generative Model : Latent Variable Model
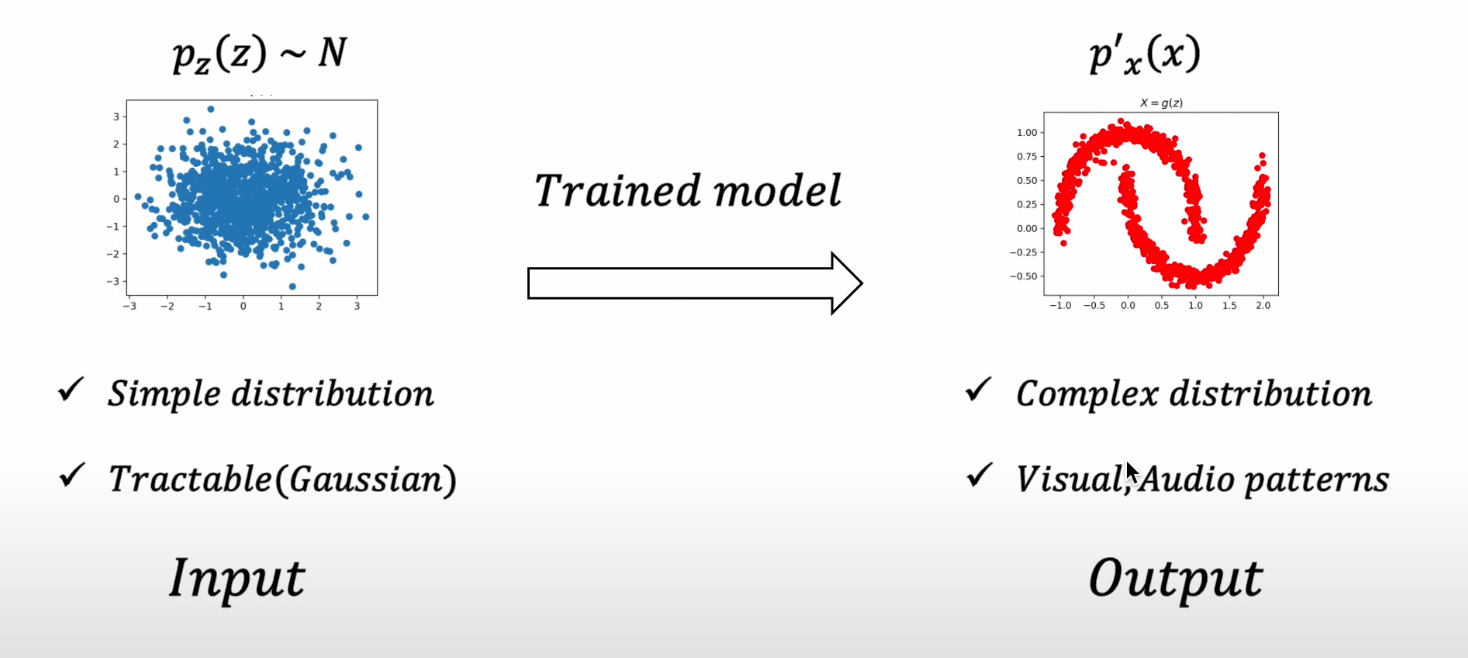
-
결국 생성 모델로부터 원하는 것은 매우 간단한 분포(z)를 특정한 패턴(오른쪽)을 갖는 분포로 변환(mapping, transformation, sampling) 하는 것
-
그렇기에 대부분의 생성모델이 주어진 입력 데이터로부터 latent varicable(z)를 얻어내고, 이를 변환하는 역량을 학습하고자 함
VAE
1) 학습된 Decoder Network를 통해 Latent Variable을 특정한 패턴의 분포로 Mapping
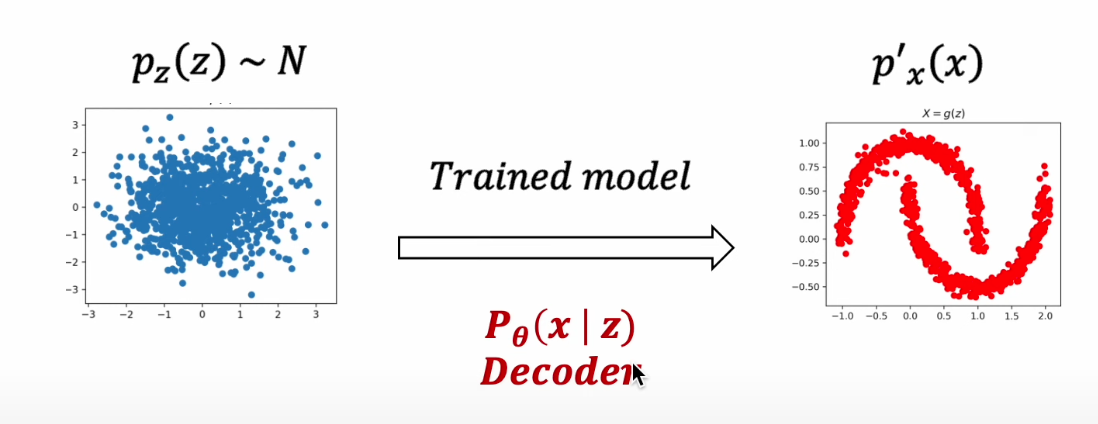
2) Encoder 를 모델 구조에 추가해, Latent Variable / Encoder, Decoder 를 모두 학습
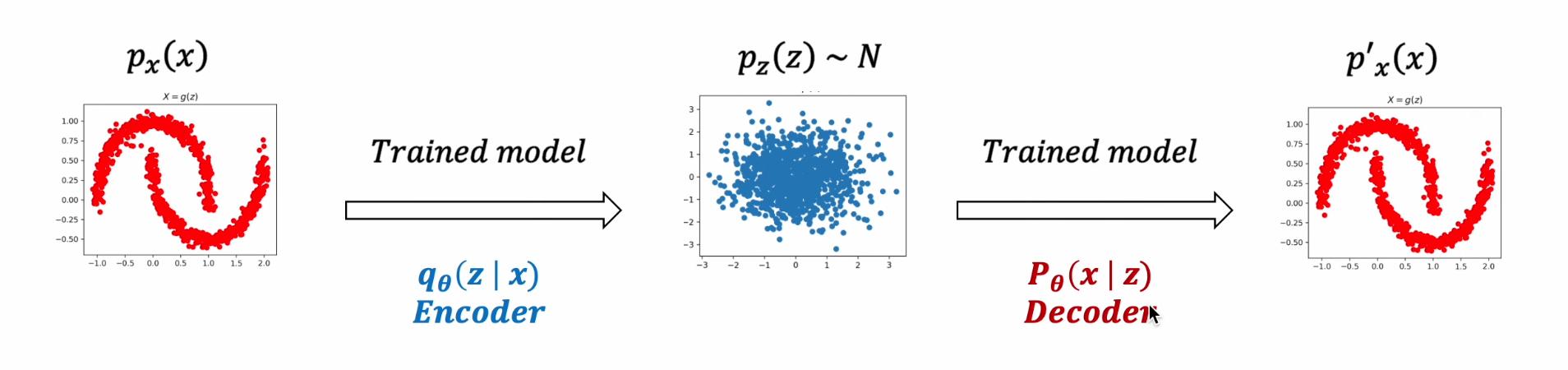
- likelihood를 극대화 시키는 Encoder, Decoder 학습
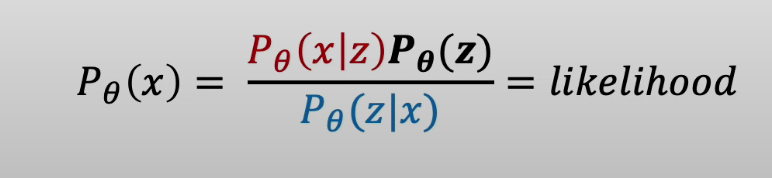
GAN
1) 학습된 Generator 를 통해 Latent Variable 을 특정한 패턴의 분포로 Mapping

2) Discriminator 를 모델 구조에 추가해, Generator를 학습
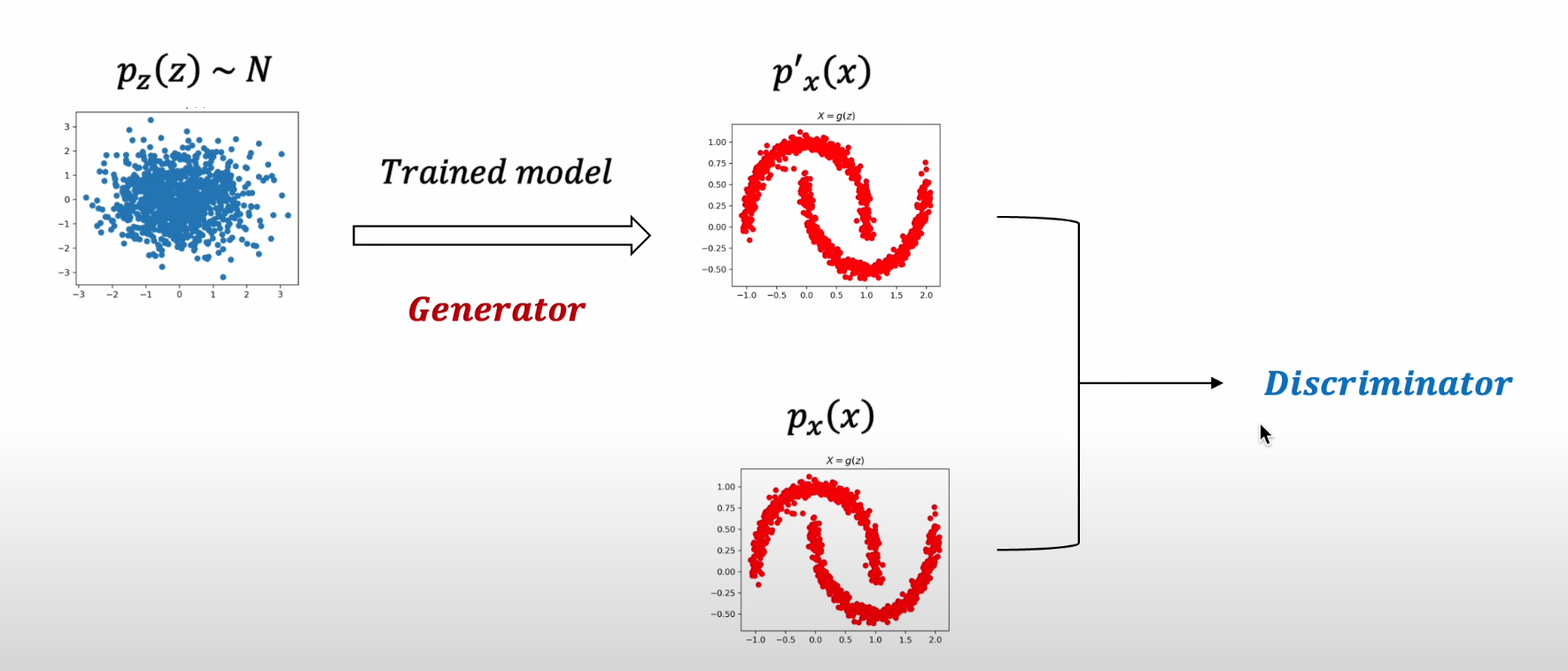
Flow-based Model
1) 학습된 Flow Model의 Inverse Mapping을 통해 Latent Variable 을 특정한 패턴의 분포로 Mapping
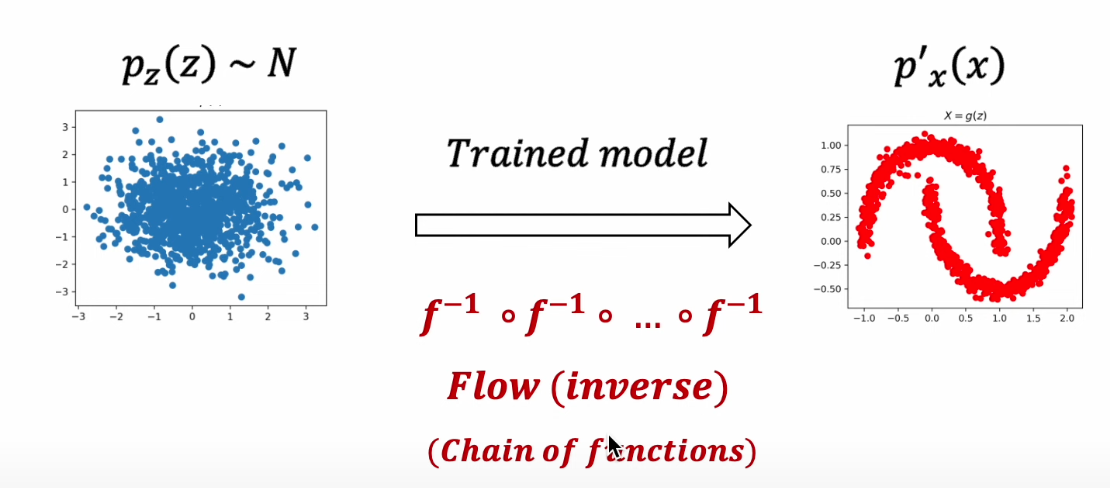
2) 생성에 활용되는 Inverse Mapping을 학습하기 위해 Invertible Function을 학습
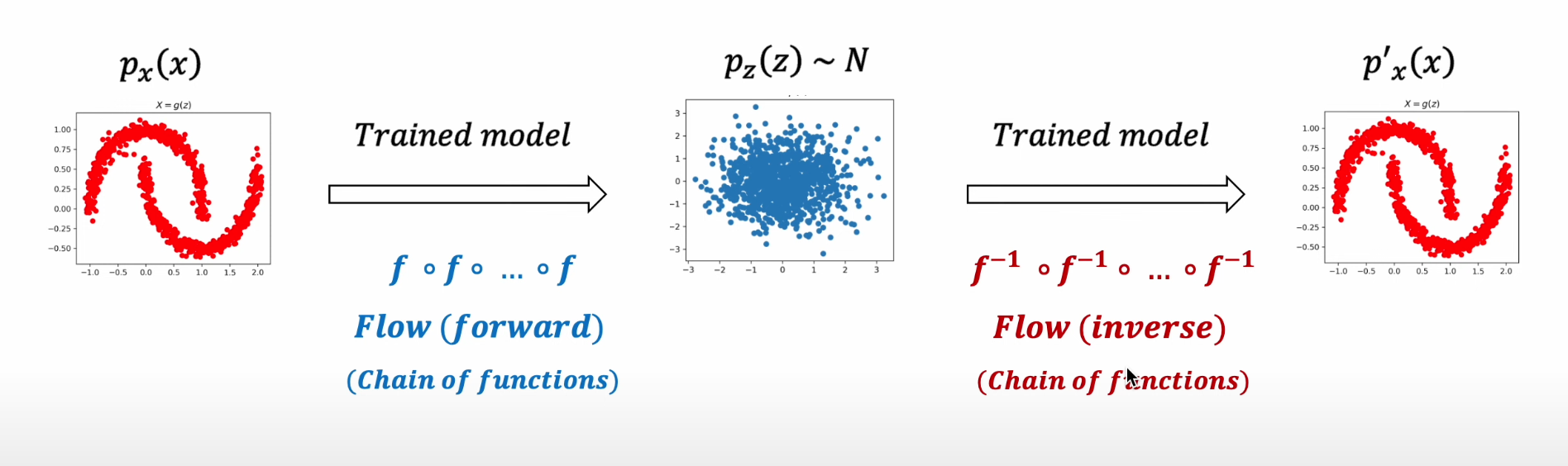
Diffusion based Generative Model
1) 학습된 Diffusion Model의 조건부 확률 분포 P(x|z)를 통해 특정한 패턴의 분포를 획득
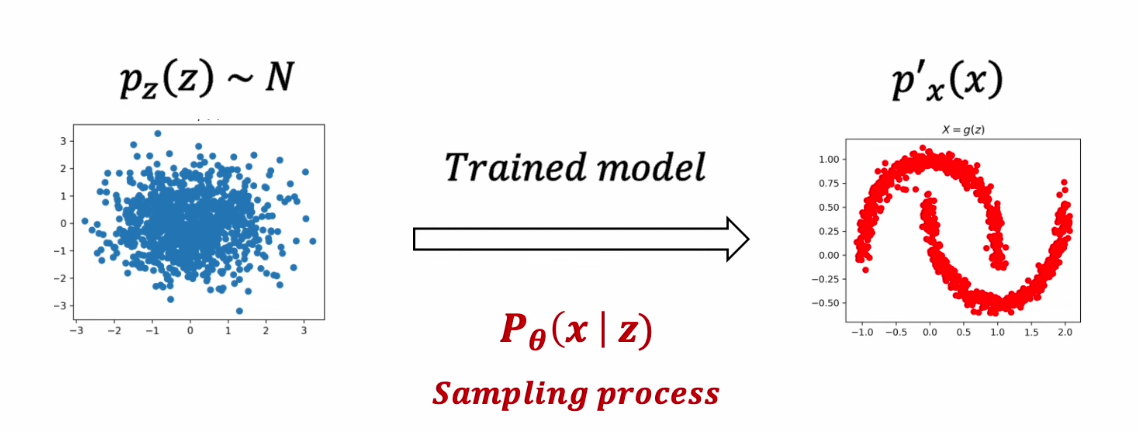
2) 생성에 활용되는 조건부 확률 분포 P(x|z) 학습을 위해 네트워크를 학습시키는 것이 아닌 , Diffusion Process q(z|x) 활용
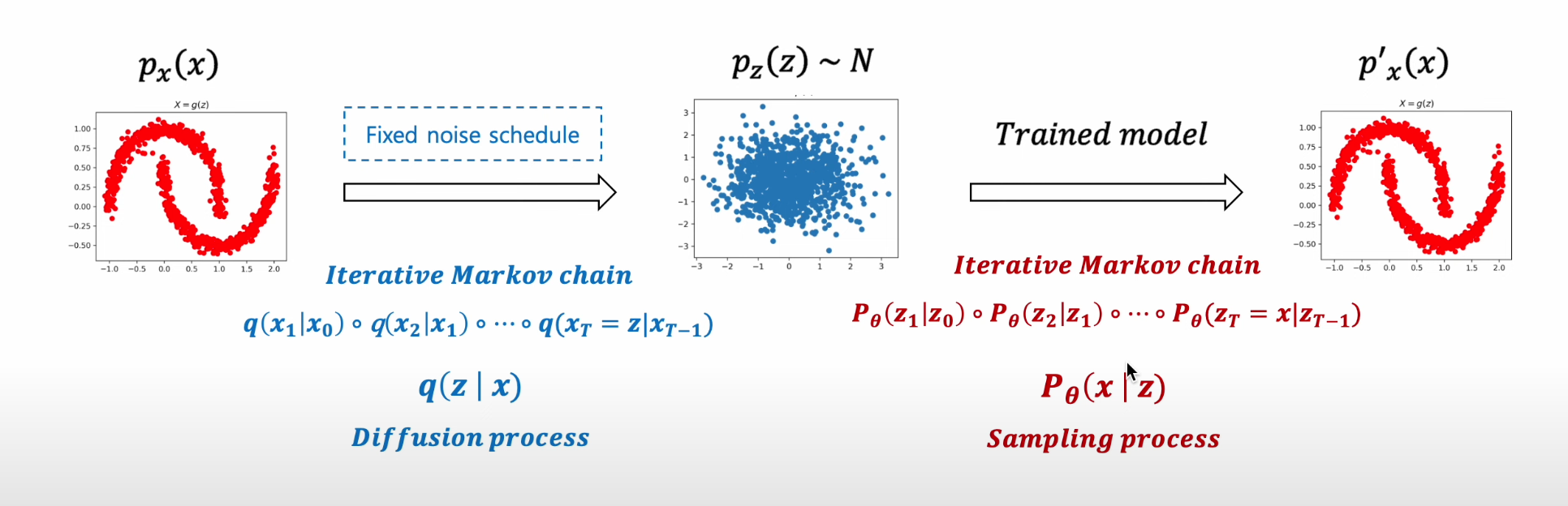
3) 즉, 다른 모델들과 다르게 Forward 과정이 학습에 포함되지 않으며, 학습의 대상은 오직 "Sampling Process"
Diffusion Model
Diffusion Model
-
Diffusion Model 은 Generative Model 로서 학습된 데이터의 패턴을 생성해내는 역할을 함
-
패턴 생성 과정을 학습하기 위해 고의적으로 패턴을 무너트리고(Nosing, Diffusion Process) 이를 다시 복원하는 조건부 PDF를 학습(Denoising, Reverse Process)
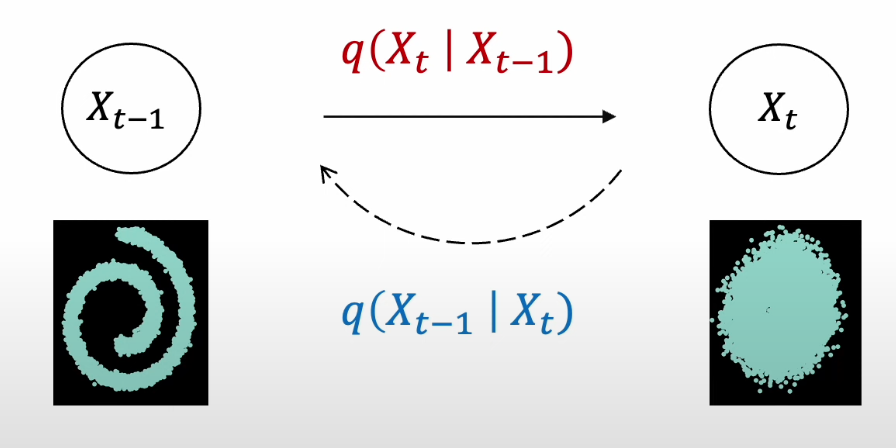
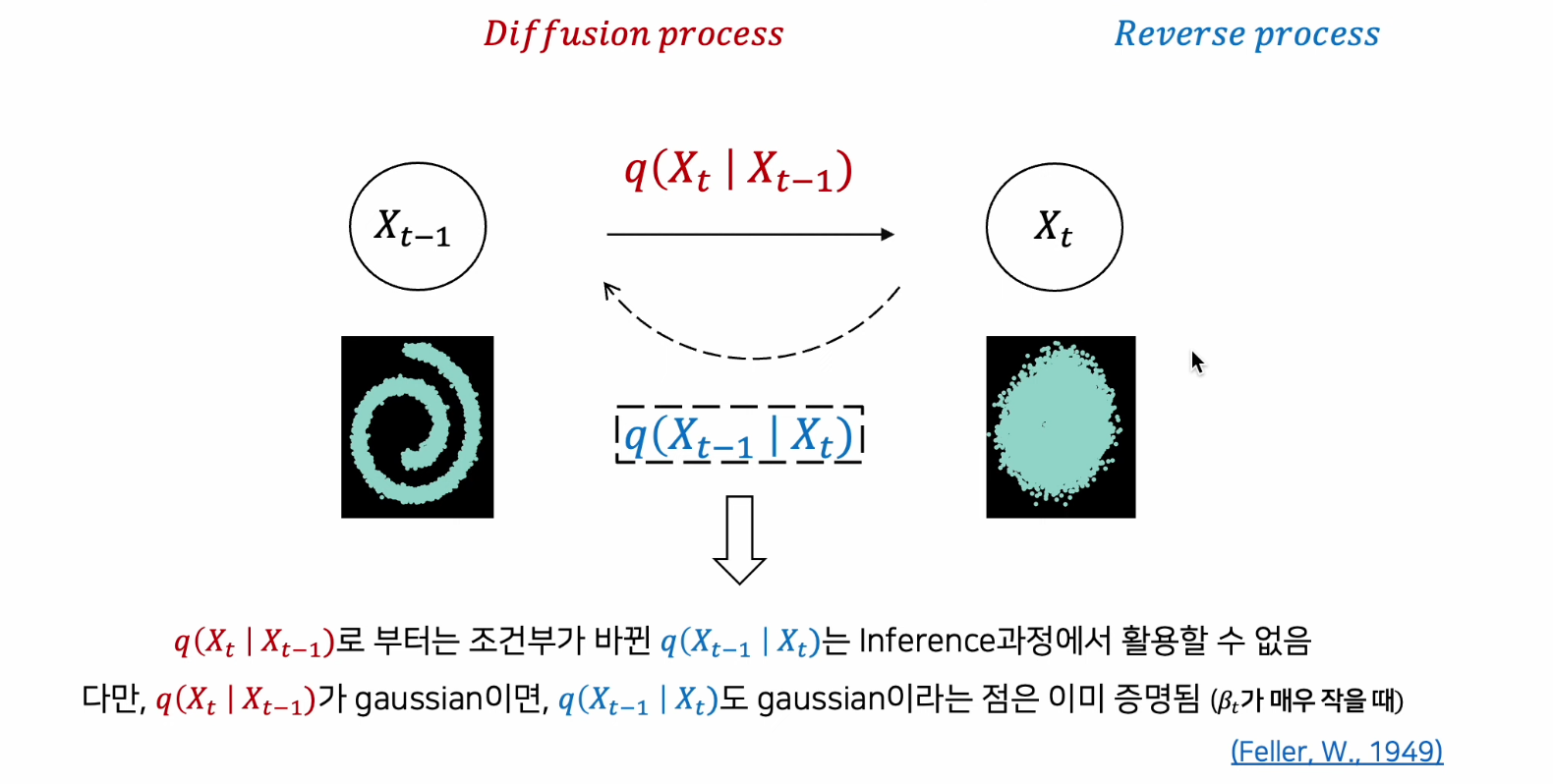
-
빨간색의 Diffusion Process는 학습이 필요 없음, 왜냐면 t시점은 t-1시점으로 사전에 정의한 Noise 형성 방법대로 만들어낼 수 있기 때문
-
1949년도 증명에 의해 결과적으로 가우시안 분포를 유지한다는 점을 파악할 수 있음
-
알지못하는 부분은 "학습"으로 이루어야 함(대략 1,000번 반복)

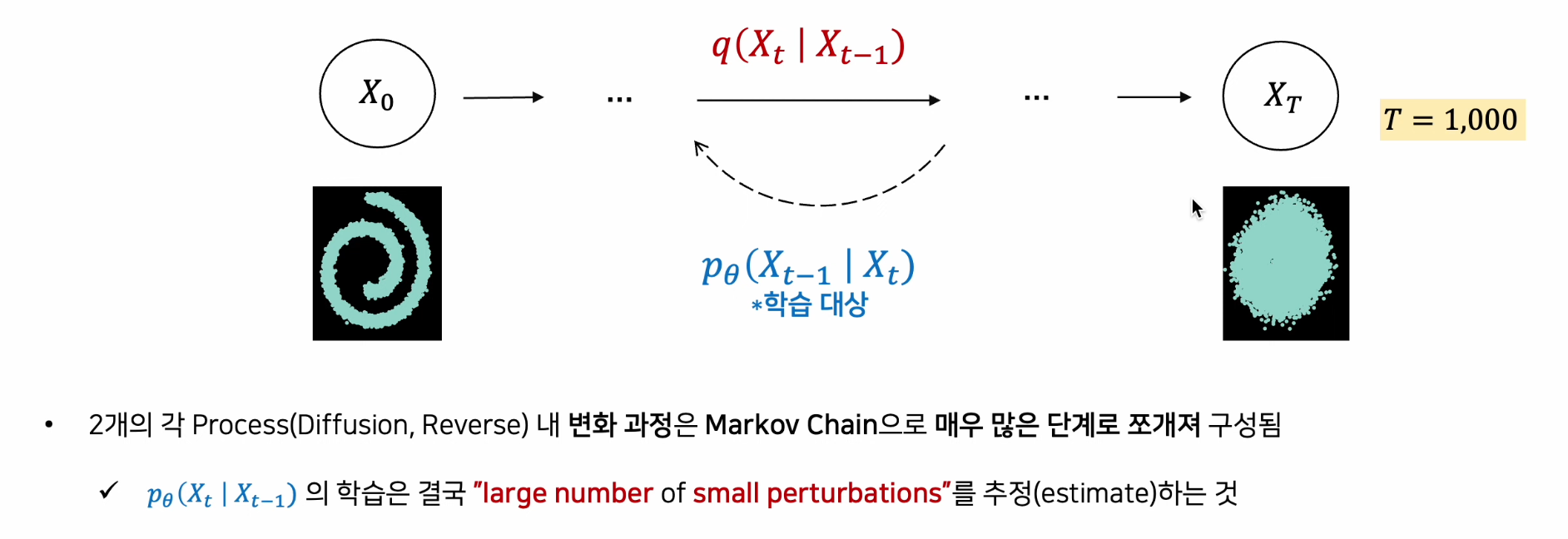
-
정리 : Diffusion Process, Reverse Process 모두 조건부 가우시안 분포를 갖는 마르코브 체인이다.
3. Diffusion Model
Phase 1 - Diffusion Process(Forward)
-
Diffusion Process는 Gaussian Noise를 점진적으로 주입하는 과정
-
Diffusion Process는 조건부 가우시안 q(Xt|Xt-1)의 Markov Chain으로 구성됨

-
주입되는 Gaussian Noise 크기는 사전적으로 정의되고, 이를 베타t로 표기
= 사전적으로 정의되기 때문에 학습이 필요 없음
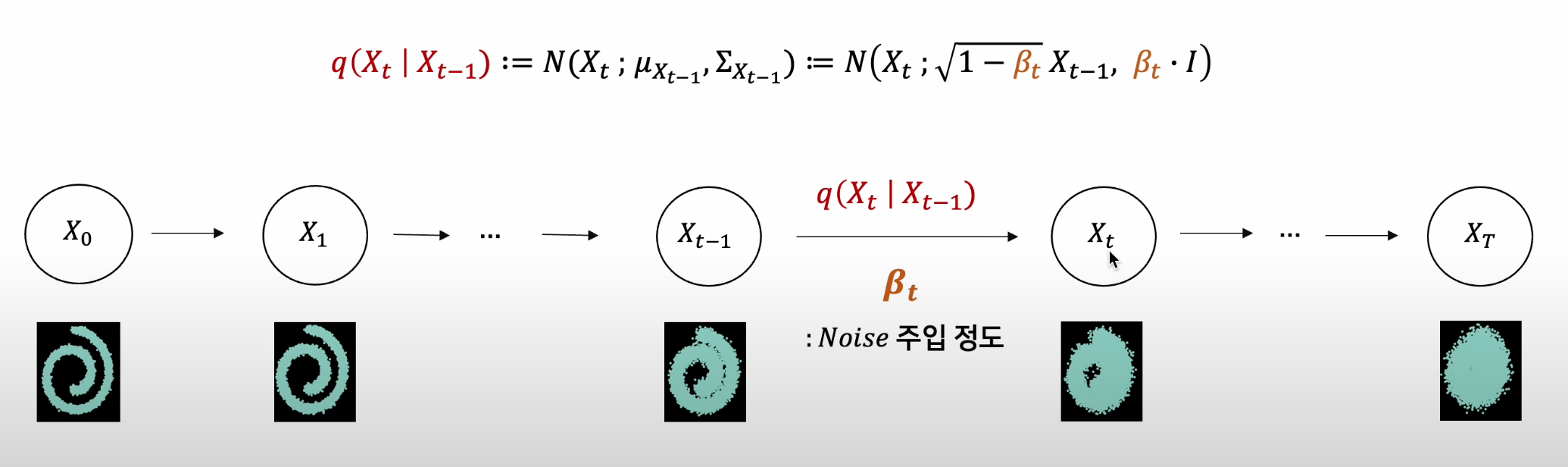
- 위 이미지와 같이, 베타t가 커질수록 점차적으로 가우시안 분포가 됨
- (J's 의문) 학습이 필요가 없으면, 이 과정이 왜 필요한거지..?
-
베타t의 사전적 정의 방법(Scheduling)
1) Linear Schedule
2) Quad Schedule
3) Sigmoid Schedule
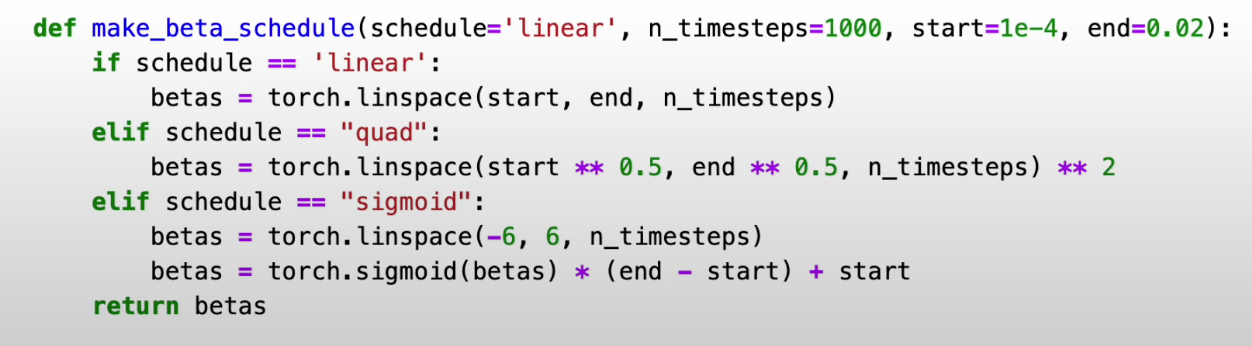
-
CelebA Sample에 Noise Scheduling 적용하면 다음과 같은 결과가 나옴
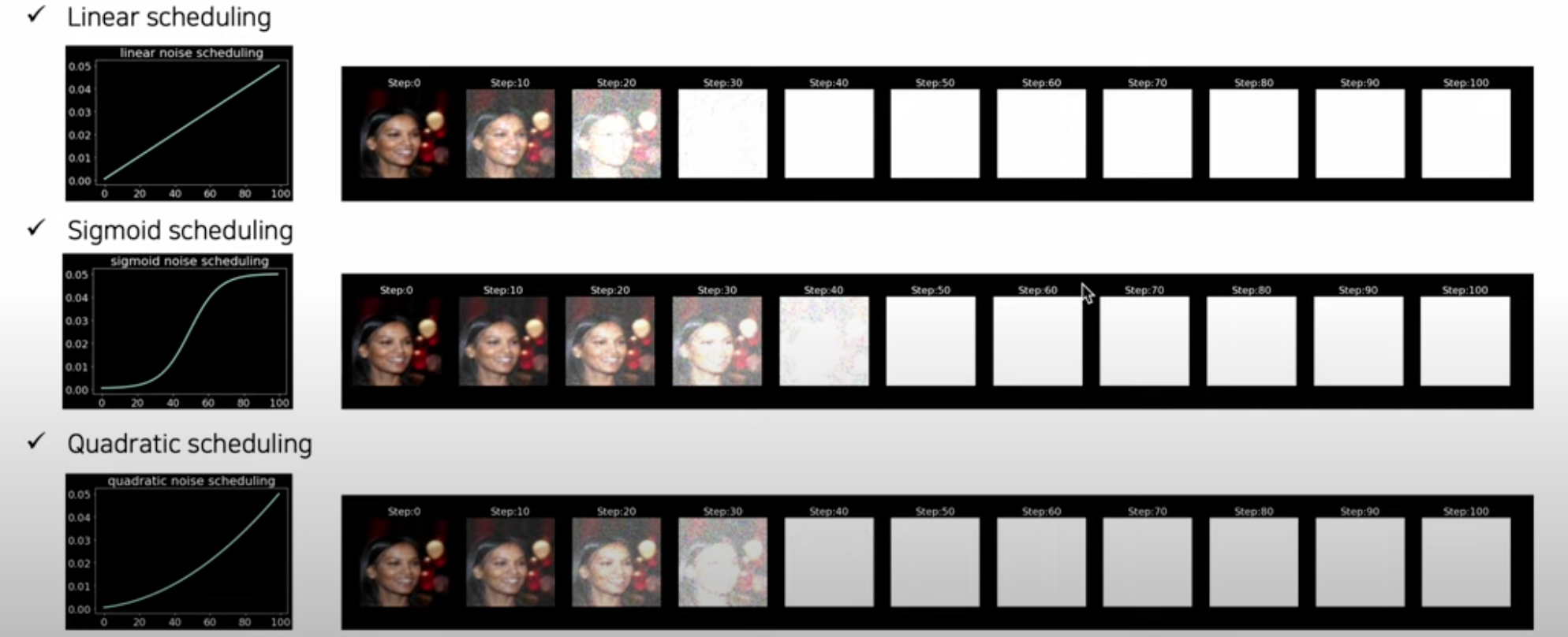
-
노이즈가 주입되며 이미지가 점점 사라짐
-
Code(VAE와 유사)

-
Latent Variable의 관점에서 Diffusion Process
- Diffusion Process는 점진적으로 단계적 Gaussian Noise를 갖는 다수의 Latent Variable을 획득
- 다수의 Latent Variable을 상정한ㄴ다는 점에서 Hierarchical VAE와 유사한 접근
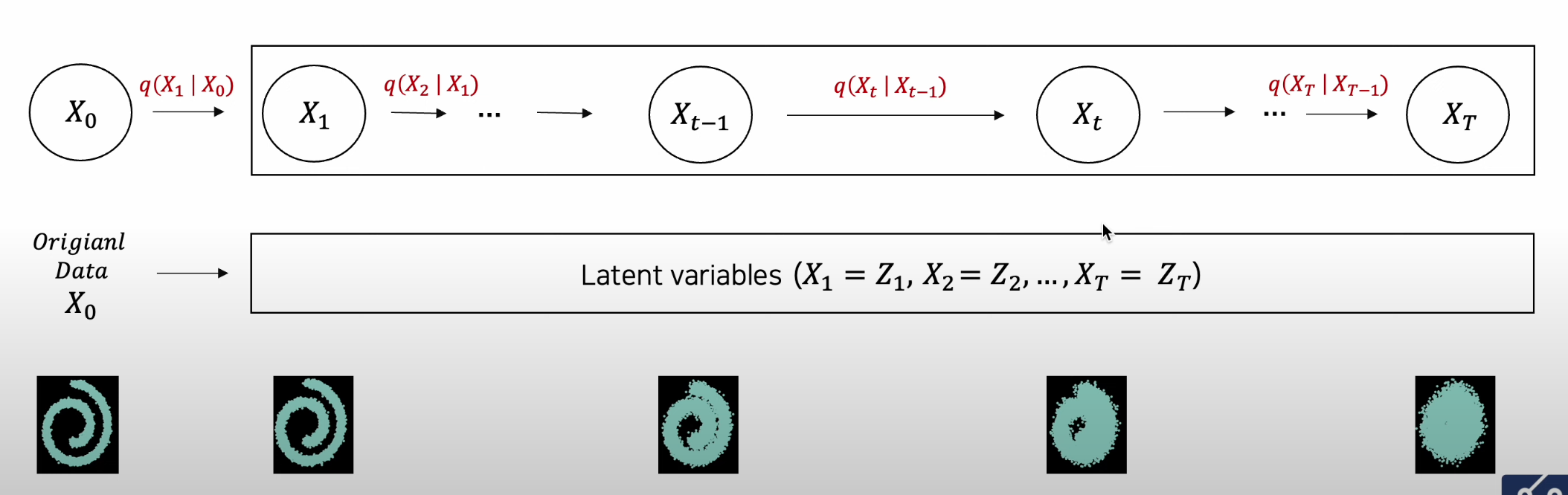
-
Dissution Process 는 Conditional Gaussian 의 Joint-Distribution 으로서, X_0을 조건부로 Latent Variables를 생성해내는 과정
-
가장 마지막 Latent Variable(X_T=Z_T)로 Pure Isotropic Gaussian을 획득

Phase 2 - Reverse Process
Remind
- Diffusion Model은 Generative Model로서 학습된 데이터의 패턴을 생성해내는 역할을 함
- 패턴 생성 과정을 학습하기 위해 고의적으로 패턴을 무너트리고, 이를 다시 복원하는 조건부 PDF를 학습함
- Reverse Process는 Diffusion Process 의 역 과정(Denoising)을 학습
Reverse Process
-
결과적으로 가우시안 분포인점은 같음
-
Diffusion Process 분포는 알고 있는 분포, Reverse Process는 알지 못하는 분포라는 점이 다름
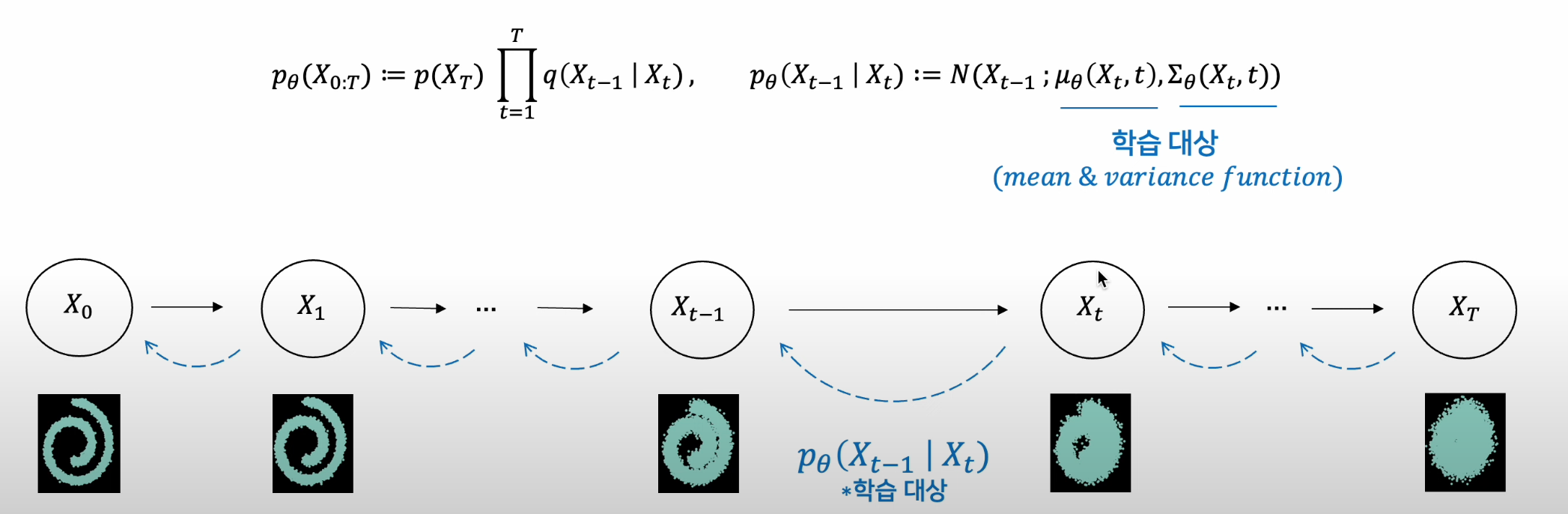
-
즉, Mean, Var을 학습해야 함

-
Loss(블로그에서 도출 과정 참고)
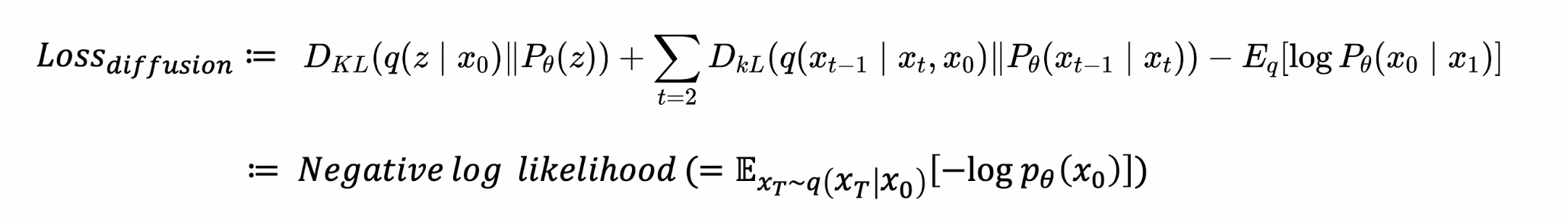
-
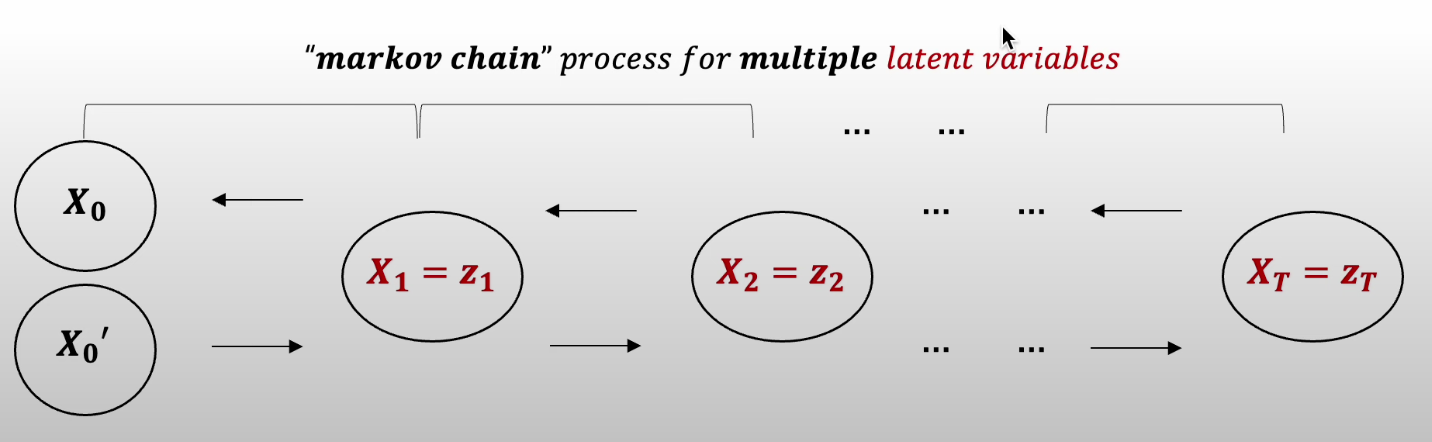
VAE와 Diffusion 의 구조 비교
-VAE : 하나의 Latent Variable 도출을 목표로 함
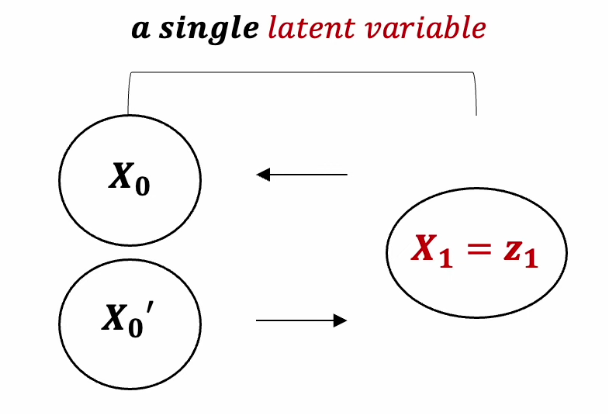
-
Diffusion : t-1개, 즉 여러 개의 Latent Variable 도출을 목표로 함
-
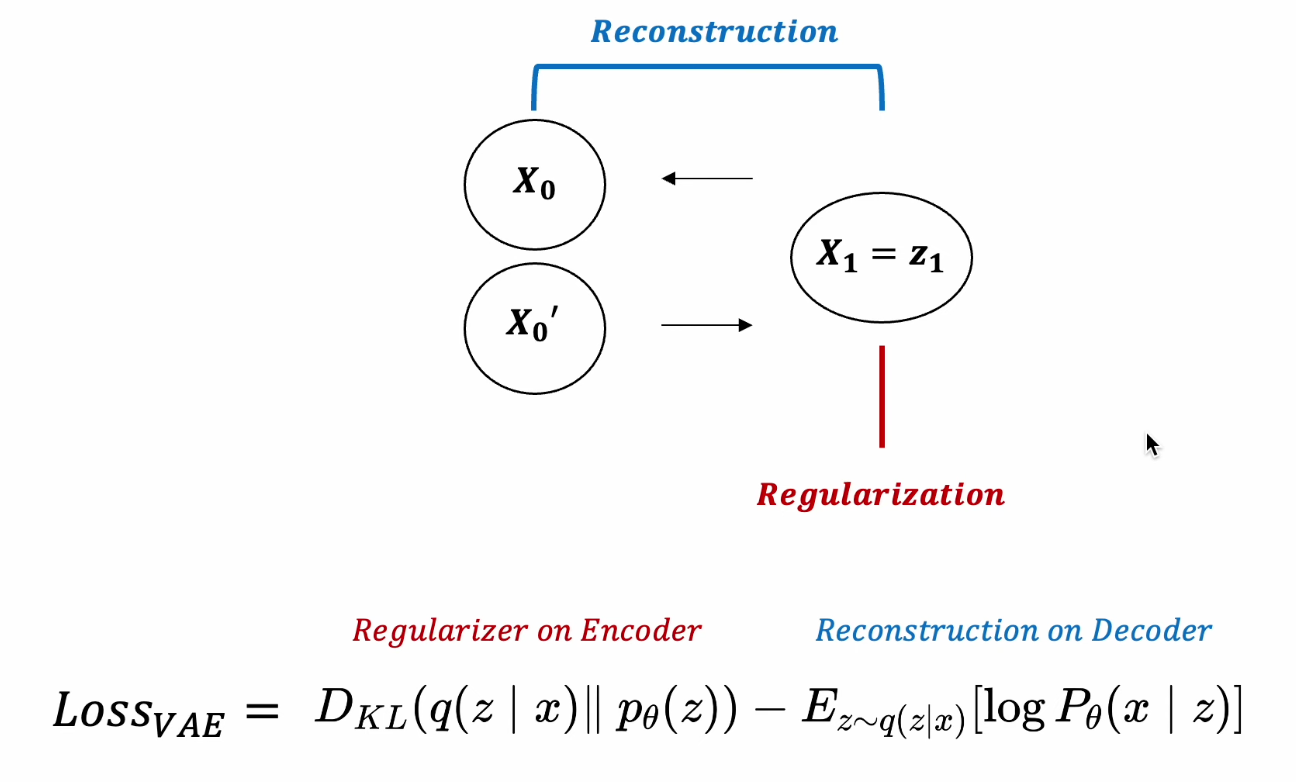
VAE Loss :
- Reconstrucion Term, Regularization Term
-
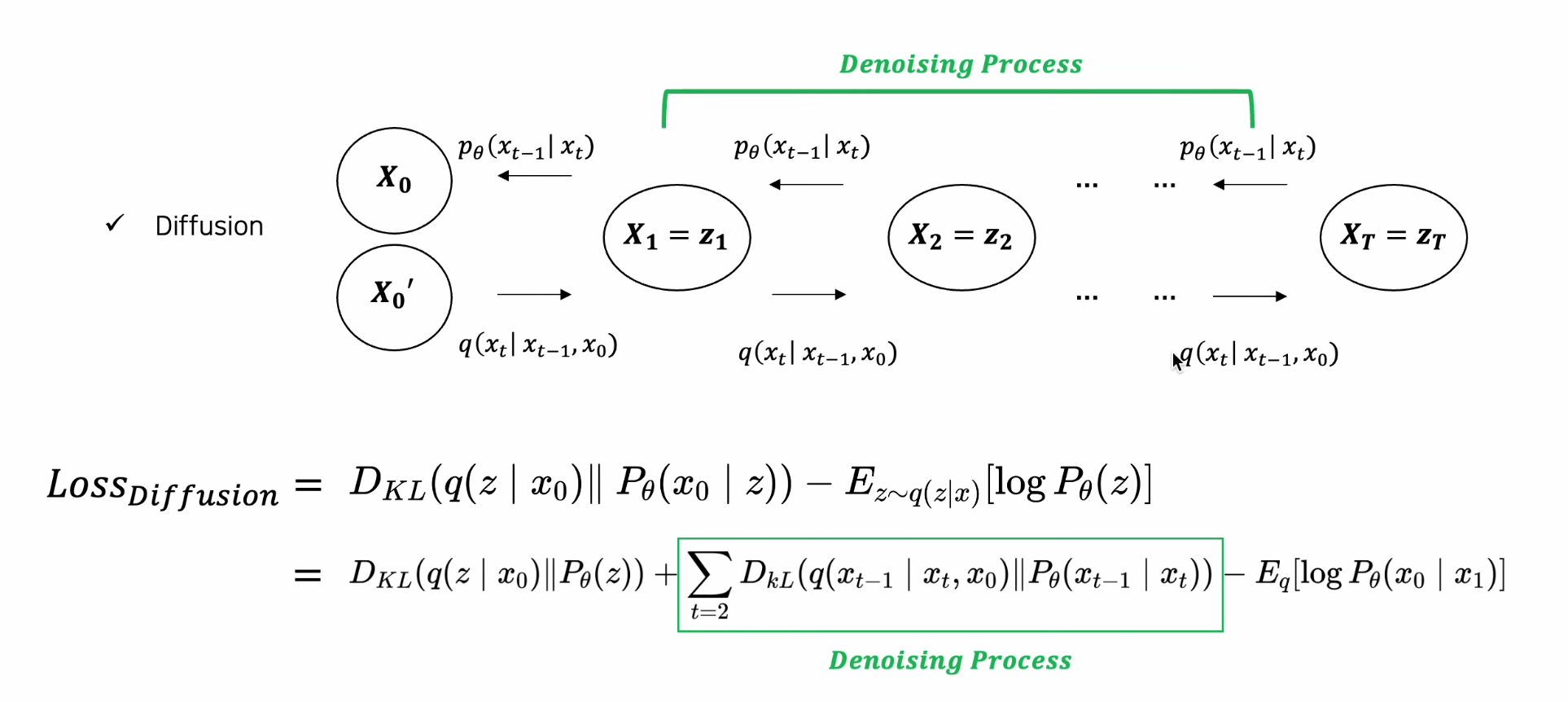
Diffusion Loss :
- VAE와 공통 Reconstruction Term, Regularization Term

- VAE와 차이 : 마르코브 체인 만들어나가는 과정
-
Diffusion All Loss :
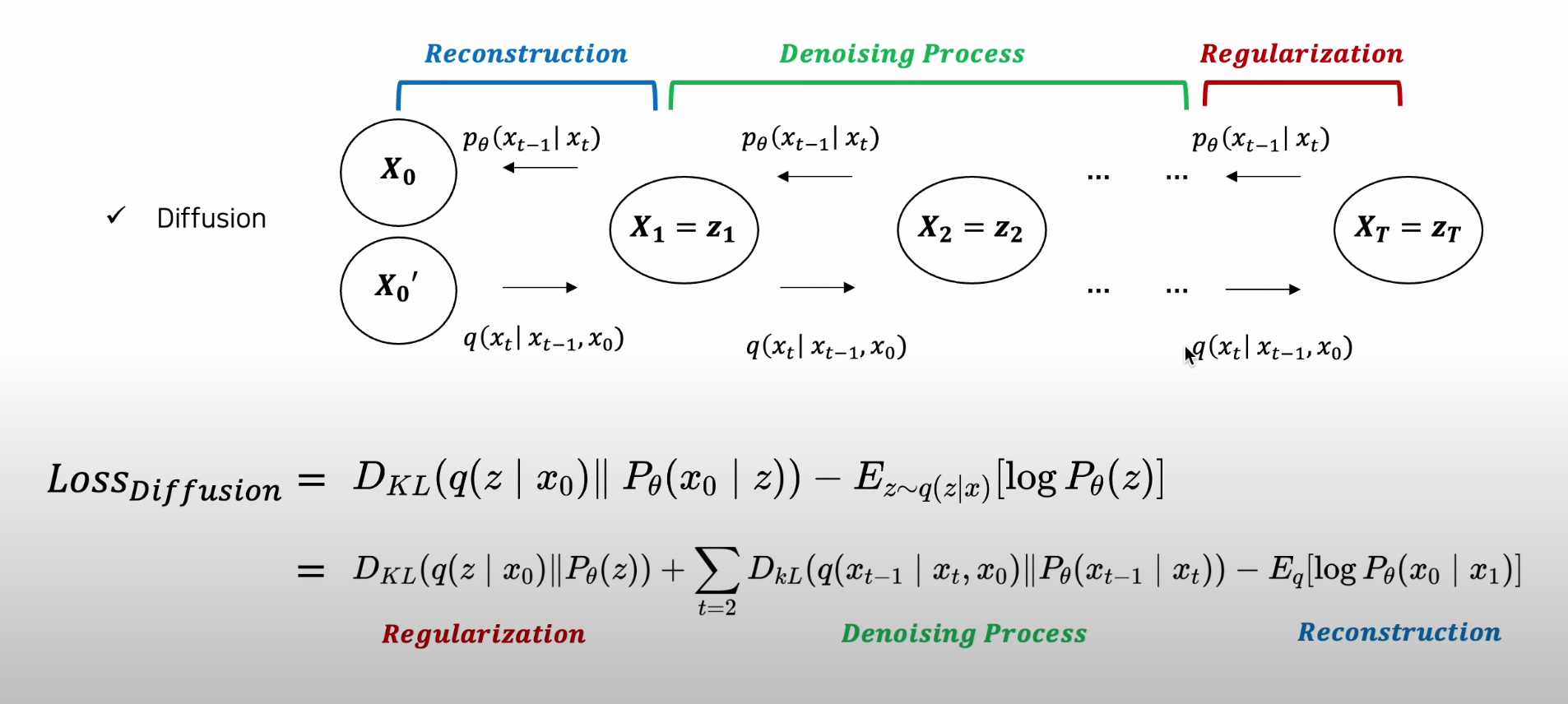
-
VAE vs. Diffusion Loss

4. DDPM 2020
DDPM Loss
- DDPM 연구에서는 Loss가 굉장히 간단한 식으로 정의됨(성능 향상됨)

DDPM Loss에서의 변화
1) 학습 목적식에서 Regularization Term 제외(즉, Bt를 고정함)
- 굳이 학습시키지 않아도 fixed noise scheduling으로 필요한 isotropic gaussian 을 획득할 수 있기 때문
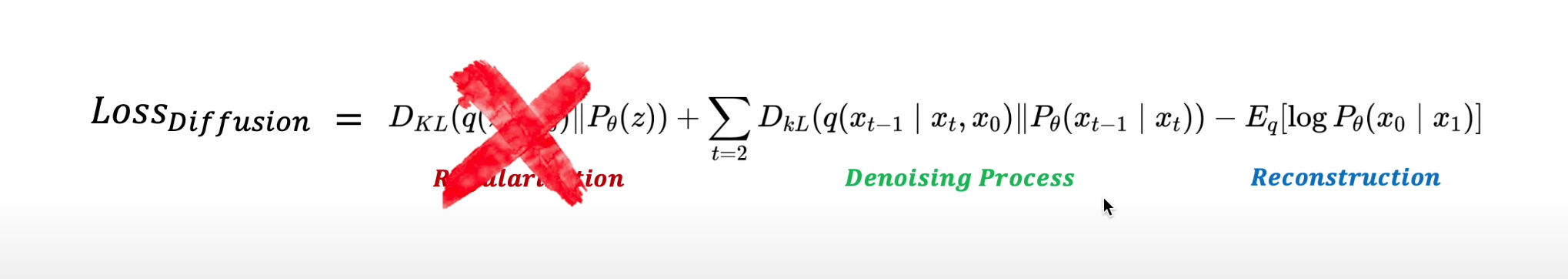
2) Denoising Processs 의 목적식 재구성
- 학습 대상을 평균과 분산이 아닌 평균으로 재구성(분산 제외)
- 주입된 노이즈 사이즈는 이미 알고 있기 때문에, 알고 있는 분산 활용(상수화)

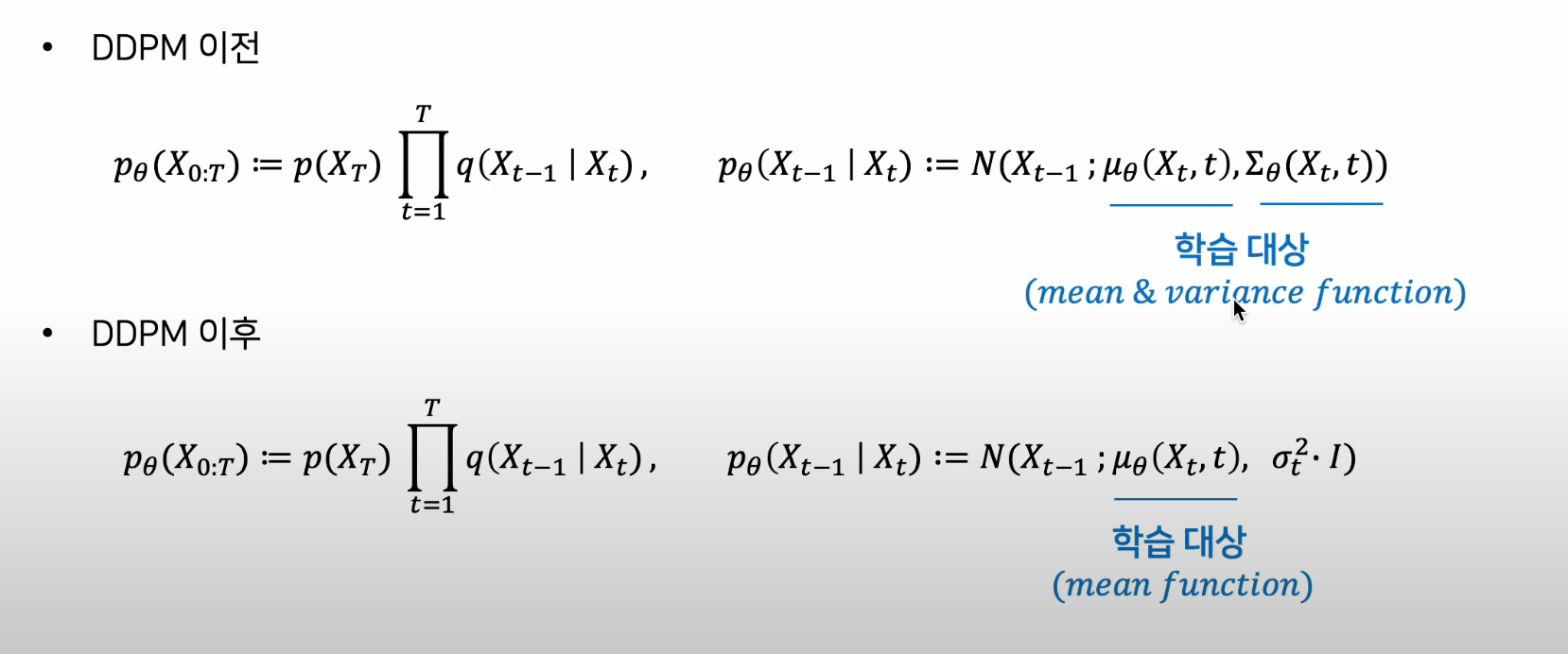
-
기존의 Denoising Process를 평균관점에서 새롭게 정의
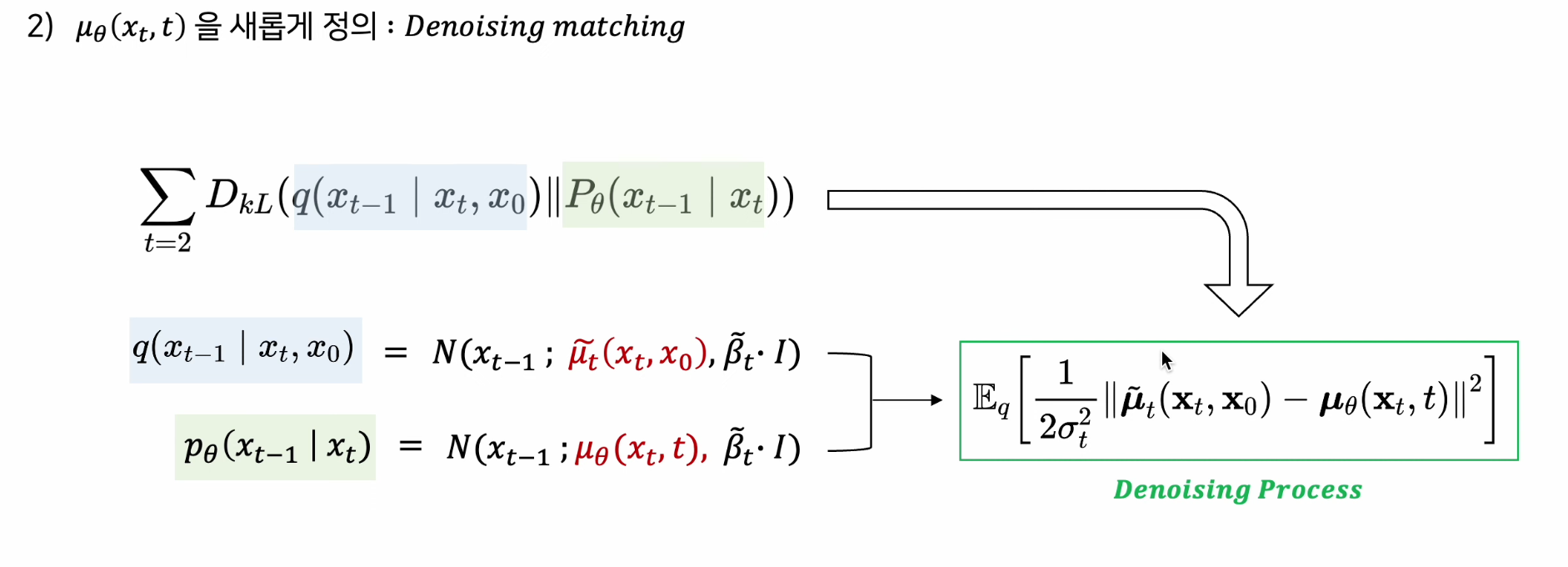
가장 큰 Contribution

-
Loss Term을 점점 간소화하여 Noise Estimation의 모습이 됨


5. DDPM 2020 : Experiments
Sample Quality
-
이미지 데이터에 적용 결과
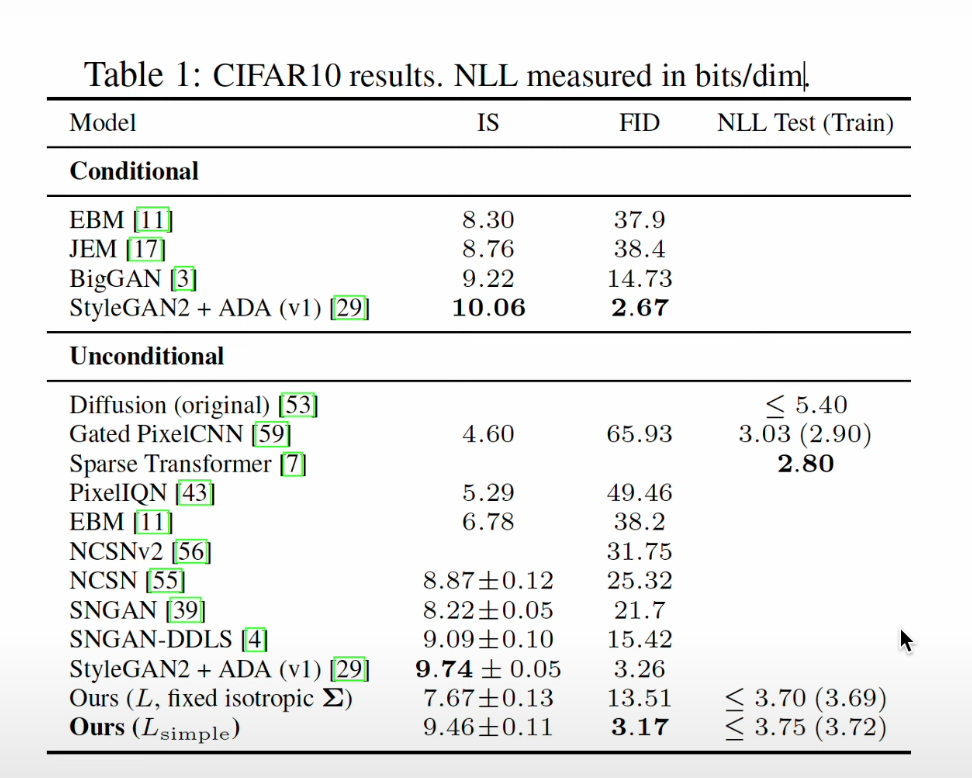
- Unconditional Generative Model 중 가장 높은 FID
- 계수 Term 을 제외한 경우는 제외하지 않은 경우보다 NLL이 조금 높지만, FID는 월등히 높음
Ablation Study for 'Objective Function'

-
learned diagonal : Noise 크기를 학습시킨 경우
-
Mean 예측 목적식보다 앱실론 예측 목적식에서 성능 향상에 크게 기여
-
왜 이런 결과가 도출되는가

출처 : 2022. 07. 11 고려대학교 산업경영공학부 DSBA 연구실
PPT : https://drive.google.com/file/d/1nCvM8VJo4CkeBFicpbOGJwv-6KR7jetj/view
