[알고리즘] 문자열, 투포인터, 그리디(Greedy)

timdalxx·2022년 2월 20일

algorithm

목록 보기

4/5

01 | 문자열

1. 해싱

필요성

디렉토리와 파일 : 파일시스템은 하나의 디렉토리에 존재 가능한 파일의 수에 제한이 없기때문에 디렉토리마다 대량의 파일이 존재할 수 있음
디렉토리 내 존재하는 파일 나열하거나, 존재 유무 판별 등에 사용될 검색기능은 시스템 성능 저하의 원인이 될 수 있음

해싱

특정 항목 검색 시, 탐색 키에 대한 산술적 연산으로 키가 있는 위치를 계산하여 바로 찾아가는 방법

방법

직접 번지 테이블(배열) : 전체 키들의 집합이 작은 경우 효율적
- 단점 1 : 키값의 집합이 클 때, 현실적인 컴퓨터 메모리 공간에서 테이블 생성 불가
- 단점 2 : 실제 키 집합이 전체 키 집합보다 상대적으로 작아 메모리 공간 낭비
해시 테이블 : 전체 집합에 비해 실제 사용되는 키(K)들의 집합이 작을 때 효율적
- 장점 : 직접 번지 테이블보다 메모리 공간이 적게 필요(= O(|K|)
- 해시 함수 : 키 값 k의 자료를 저장할 위치를 계산함
- 충돌(Collision) : 서로 다른 키값을 해시 함수에 적용할 때, 반환된 해시 함수가 동일한 경우
- 충돌 해결 방법
  1. 체이닝(Chaining) : 해시 테이블의 구조를 변경하여 각 버킷에 하나 이상의 키 값을 가지는 자료가 저장될 수 있도록 하는 방법(연결 리스트 활용)
  1. 개방 주소법(Open Address) : 해시 함수로 구한 주소에 빈 공간이 없어 충돌이 발생하면 그 다음 위치에 빈 공간이 있는 지 조사하는 방법

2. 문자열 매칭

문자열 처리

정보 검색, 통신 시스템, 프로그래밍 시스템, 유전체학 등 종류가 다양하며 많은 응용 분야에서 매우 중요한 요소로 쓰임

정보 검색 : 키워드 기반의 웹페이지 검색

통신 시스템 : 텍스트 메시지, 이메일 전송, 전자책 다운로드 등

문자열 매칭(패턴 매칭)

텍스트 문자열(t)에 패턴 문자열(p)이 포함되어 있는지 찾는 것

1) 고지식한 패턴 검색 알고리즘

본문 문자열을 처음부터 끝까지 차례대로 순회하면서 패턴 내의 문자들을 일일이 비교하는 방식의 알고리즘
하나씩 비교하다가 일치하지 않는 경우가 나타나면 다음 문자로 옮겨 다시 일일이 비교
패턴은 항상 처음에 시작하며, 텍스트의 시작은 이전 시작의 다음 위치
최선의 경우 : O(N) - 적어도 한 번씩 훑어봄
최악의 경우 : 패턴을 찾지 못한 경우, 텍스트의 모든 위치에서 패턴 비교 필요(= O(MN)) (M : 패턴의 길이, N : 텍스트의 길이)

2) 카프-라빈(Karp-Rabin) 알고리즘

문자열 검색을 위해 해시 함수를 이용하는 알고리즘
평균적으로 선형에 가까운 빠른 속도를 가짐
패턴의 해시 값과 텐스트 내의 패턴의 길이만큼 문자열에 대한 해시 값 비교
고려 사항
- 처음 해시 값을 구할 때, 찾고자 하는 문자열에서 패턴 길이만큼 읽어 구함
- 패턴의 길이가 커지면 길이를 일정 자릿수로 맞추기 위해 모듈러연산을 취해 줌
- 해시 값이 일치할 경우 실제 문자열이 일치하는 지 검사
최선의 경우 : O(N) - 적어도 한 번씩 훑어봄
최악의 경우 : O(MN)

3) KMP(Knuth-Morris-Pratt)

Knuth, Morris, Pratt 가 제안한 알고리즘
불일치가 발생한 텍스트 문자열 앞에 어떤 문자가 있는지 알고 있어 재비교 불필요
불일치가 발생하면 다음 비교 위치를 미리 계산하여 불필요한 시작을 최소화
매칭이 실패했을 때 돌아갈 곳을 알 수 있음
최선의 경우 : O(N) - 적어도 한 번씩 훑어봄
최악의 경우 : O(M+N)

4) 보이어-무어 알고리즘

대부분의 상용 소프트웨어에서 채틱하고 있는 알고리즘
오른쪽 끝에서 왼쪽으로 문자열을 비교(앞부분보다 끝부분에 불일치가 일어날 확률이 높기때문)
패턴의 오른쪽 끝 문자에서 불일치 발생 시, 텍스트이 문자가 패턴 내에 없으면 이동거리 = 패턴 길이
최선의 경우 : 일반적으로 O(N) 보다 시간 소요가 적음
최악의 경우 : O(MN)

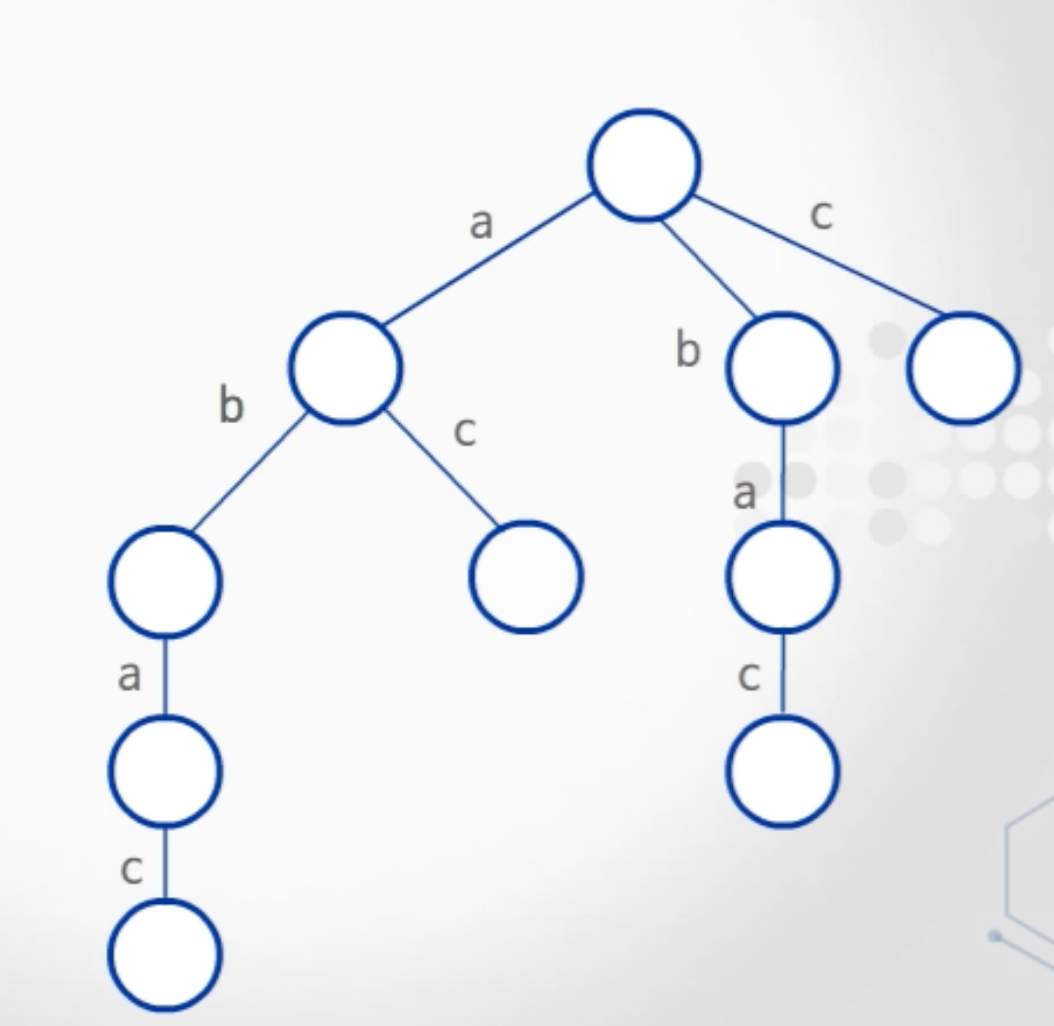
3. 트라이

트라이(Trie)

문자열의 집합을 표현하는 트리(Tree)
정보 검색(Retrieval)에서 이름을 따옴

접미어 트라이

문자열의 모든 접미어를 Trie로 표현한 것

부분 문자열 검사 쉬움
두 접미어의 최장 공통 접두어 찾기 가능
사전적 순서로 정렬된 k번째 접미어 찾기 가능

4. 접미어 트리

접미어 트리(Suffix Tree)

문자열 연산에 필요한 알고리즘을 빠르게 구현 가능
응용 : 문자열 매칭, 부분문자열 매칭, 최장 공통 부분문자열

압축된 트라이(Compressed Trie)

노드와 간선을 부분 문자열로 압축함(자식이 하나만 있는 노드를 하나의 간선으로 표현)

5. 접미어 배열

접미어 배열

텍스트의 접미어를 사전적으로 나열한 배열
접미어 트리보다 메모리 사용에는 효율적이지만 느림
응용 : 텍스트 인덱싱, 데이터 압축, Bio-informatrics

장점

생성 방법이 접미어 트리에 비해 간단
적은 메모리로 구현 가능 : 2개의 선형 크기의 배열로 구성되며 전형적으로 접미어 트리에 비해 1/4 크기의 메모리를 사용한다고 알려져 있음

LCP 배열

접미어 배열의 보조적 자료 구조
최장 공통 접두어에 대한 정보를 저장하는 배열
- 정렬된 접미어 배열에서 연속적인 두 개의 접미어들 사이의 최장 공통 접두어의 길이를 저장
- 접미어 배열의 순회나 패턴 매칭을 효율적으로 수행하는 데 사용

6. 압축

압축의 활용과 중요성

텍스트, 이미지, 음원, 영상 데이터 등 거의 모든 응용 분야에서 사용됨
데이터 압축의 주요 이유 : 저장공간 절약, 전송 시간 단축

압축률 = C(D)의 비트 수 / D의 비트수 = 압축 데이터의 비트 수 / 복구된 원본의 비트 수

압축률에 따라 무손실 / 손실 압축으로 분류 가능

Run-Lenth Decoging

동일한 값이 몇 번 반복 되는가를 나타내는 방식
ex) ABBBBBBBCC -> A1B7C2

Huffman Code

구성 개념 : 기호의 빈도(전체 데이터 안에서 기호가 차지하는 비율), 허프만 트리(각 기호에 이진 코드를 부여하기 위해 생성하는 이진 트리)
고정 길이 코드 : 기호에 대응하는 코드값의 길이가 똑같은 코드 체계
접두어 코드 : 가변 길이 코드의 한 종류, 어느 코드가 다른 코드의 접두어가 되지 않는 코드 체계
탐욕 알고리즘 기법으로 허프만 트리를 생성 가능
생성 과정 : 노드만 있다고 가정 > 해 선택 > 실행 가능성 검사 > 해 검사

02 | 투 포인터(Two Pointers)

투 포인터

리스트에 순차적으로 접근해야 할 때, 두 개의 점의 위치를 기록하면서 처리하는 알고리즘
정렬된 리스트에 두 개의 포인터를 이용하여 순차적으로 접근하면서 두 개의 포인터 구간의 값 = 타겟 값이 될 때 까지 포인터를 조작하는 기법

문제 분석 및 풀이

1806

import sys
input = sys.stdin.readline

n, s = map(int, input().split())
data = list(map(int, input().split()))

result = 100000
interval_sum = 0
end = 0

for start in range(n):
	# start 는 0부터 시작
	# 현재 부분 합이 s보다 작을 때 end 증가
    while interval_sum < s and end < n:
        interval_sum += data[end]
        end += 1
	
    # 현재 부분 합이 s보다 크거나 같으면 카운트하고 start 증가
    if interval_sum >= s:
    # s보다 같거나 크면 길이가 최소인지 확인
        result = min(result, end - start)

    interval_sum -= data[start]

if result == 100000:
    print(0)
else:
    print(result)

일반적인 방법이 불가한 이유

수열의 길이(N)이 100,000일 때, 모든 부분합의 개수는 $N^2$ 으로 비효율적이다.
부분합인 S의 범위가 1억 이하(100,000,000) 이므로 메모리상으로 초과가 발생한다.

03 | Greedy Algorithm

Greedy Algorithm

현재 상황에서 가장 좋은 것을 고르는 방법
현재의 선택이 나중에 미칠 영향은 고려 하지 않음

예시 : 거스름돈 문제

최적의 해를 구하기 위해서는 가장 큰 화폐단위를 거슬러 주면 됨
큰 거스름돈이 작은 거스름돈의 배수가 아닐 경우 그리디 알고리즘은 최적해를 보장하지 못함
정당한 해를 보장하는 선에서 그리디 알고리즘을 활용해야 함

Brute-Force

조합 가능한 모든 경우를 직접 하는 방법
문제점 : 숫자가 커질수록 시간 복잡도가 기하급수적으로 증가함
종류 : 선형구조(순차탐색), 비선형구조(BFS, DFS)

문제 분석 및 풀이

1969

n, m = map(int, input().split()) # DNA의 수 N, 문자열의 길이 M

data = []
for i in range(n):
    data.append(input()) # DNA 입력

data.sort() # 사전순으로 정렬

dna = ''

for y in range(m):
    value = {'A':0, 'C':0, 'G':0, 'T':0} # ACGT 초기화
    for x in range(n):
        acgt = data[x][y] # n번째 DNA의 m번째 문자 조사
        value[acgt] += 1
    dna += max(value, key=value.get) # m번째 자리에서 가장 빈도 수가 높은 문자열이 저장됨

answer = 0
for x in range(n):
    for y in range(m):
        if dna[y] != data[x][y]:
        # HD : 문자열이 같지 않은 경우 +1
            answer += 1

print(dna) # HD 의 합이 가장 작은 dna
print(answer) # HD 의 합

완전탐색으로 풀기 어려운 이유

c++ 코드 참고
N의 범위는 1000보다 작거나 같은 자연수, M의 범위는 50보다 작거나 같은 자연수이므로 최악의 경우 $O(M*N^2)$ 이므로 완전 탐색은 가능하지만 비효율적이다.

timdalxx

Major in Computer Vision

이전 포스트

[알고리즘] 동적 계획법(Dynamic Programming) 기초

다음 포스트

[알고리즘] 문자열, 투포인터, 그리디(Greedy)

algorithm

01 | 문자열

1. 해싱

필요성

해싱

방법

2. 문자열 매칭

문자열 처리

문자열 매칭(패턴 매칭)

1) 고지식한 패턴 검색 알고리즘

2) 카프-라빈(Karp-Rabin) 알고리즘

3) KMP(Knuth-Morris-Pratt)

4) 보이어-무어 알고리즘

3. 트라이

트라이(Trie)

접미어 트라이

4. 접미어 트리

접미어 트리(Suffix Tree)

압축된 트라이(Compressed Trie)

5. 접미어 배열

접미어 배열

장점

LCP 배열

6. 압축

압축의 활용과 중요성

압축률 = C(D)의 비트 수 / D의 비트수 = 압축 데이터의 비트 수 / 복구된 원본의 비트 수

Run-Lenth Decoging

Huffman Code

02 | 투 포인터(Two Pointers)

투 포인터

문제 분석 및 풀이

1806

일반적인 방법이 불가한 이유

03 | Greedy Algorithm

Greedy Algorithm

예시 : 거스름돈 문제

Brute-Force

문제 분석 및 풀이

1969

완전탐색으로 풀기 어려운 이유

[알고리즘] 동적 계획법(Dynamic Programming) 기초

[알고리즘][프로그래머스][코딩테스트 고득점 Kit] 스택/큐

0개의 댓글

관련 채용 정보