[알고리즘] Leetcode_200_Number_of_islands

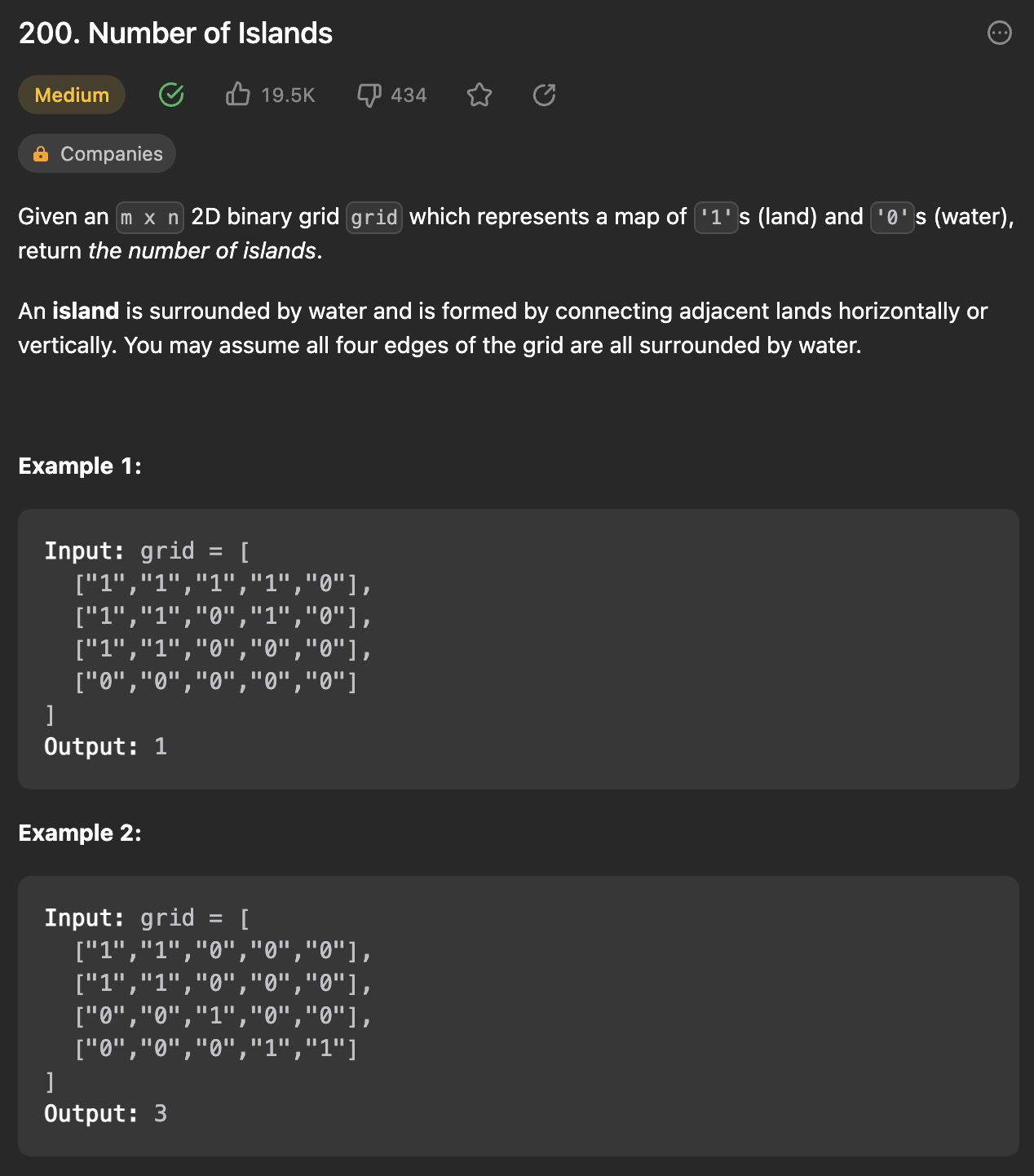
Problem

Solve

public static int numIslands(char[][] grid) {
        int island = 0;
        int m = grid.length;
        int n = grid[0].length;

        boolean[][] visited = new boolean[m][n];
        
        for(int i = 0 ; i < m ; i++){
            for(int j = 0 ; j < n ;j++){
                if(grid[i][j] == '1' && !visited[i][j]){
                    //1. BFS
                    bfs(grid, visited, i,j);
                    //2. DFS
                    dfs(grid, visited, i,j);
                    island++;
                }
            }
        }
        return island;
    }

2차원 배열을 순회하면서 1, 즉 섬을 발견하면 너비든, 깊이든 연결되어 있는 섬을 세고, 또 for문을 통해 순회를 하면서 동 떨어져 있는 넓게 분포되어 있는 섬을 찾는다.

graph 문제로 BFS(Breadth-First-Search) 너비 우선 탐색과 DFS(Depth-First-Search) 깊이 우선 탐색으로 해결할 수 있다.

BFS

시작점으로 부터 가장 가까이에 있는 정점을 순서대로 순회하면서 점점 먼 정점을 향해 순회하는 그래프 탐색 방식
-> queue 이용

//BFS
 public static void bfs(char[][] grid, boolean[][] visited, int x, int y){
        Queue<int[]> queue = new LinkedList<>();

        queue.add(new int[]{x,y});
        visited[x][y] = true;
        
        while(!queue.isEmpty()){
            int[] cur = queue.poll();
            //System.out.println("("+cur[0]+","+cur[1]+")");
            
            for(int i = 0 ; i < 4 ; i++){
                int nx = cur[0] + dx[i];
                int ny = cur[1] + dy[i];

                if(nx < 0 || nx >= grid.length || ny < 0 || ny >= grid[0].length) continue;
                if(grid[nx][ny] == '1' && !visited[nx][ny]){
                    visited[nx][ny] = true;
                    queue.add(new int[] {nx, ny});
                }
            }
        }
    }

DFS

시작점에서 부터 가장 깊게 떨어진 정점을 향해 탐색하다가 더이상 전진할 정점이 없을 경우 다시 시작점에서 다른 방향으로 깊게 나아가는 그래프 탐색 방법
-> 재귀적 recrusive

//DFS
public static void dfs(char[][] grid, boolean[][] visited , int x, int y){
        System.out.println("("+x+","+y+")");
        visited[x][y] = true;

        for(int i = 0 ; i < 4; i++){
            int nx = x + dx[i];
            int ny = y + dy[i];
            if(nx < 0 || nx >= grid.length || ny < 0 || ny >= grid[0].length) continue;
            if(grid[nx][ny] == '1' && !visited[nx][ny]){
                dfs(grid, visited, nx, ny);
            }
        }
    }

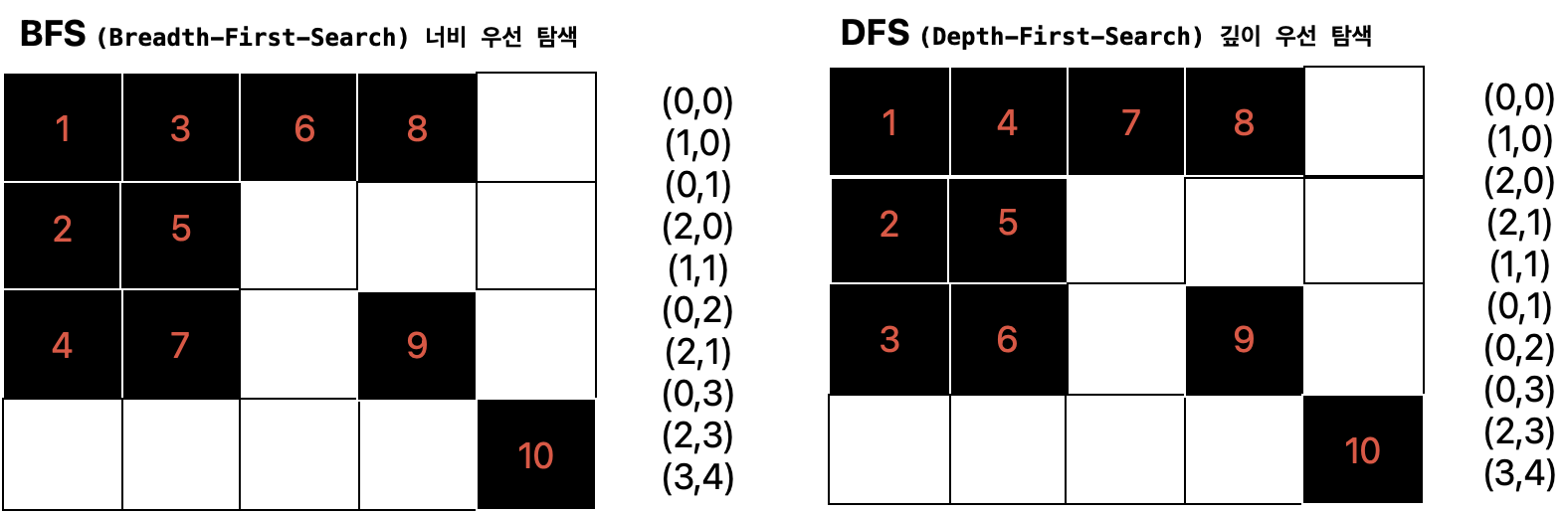
상하좌우를 순서대로 새로운 방향을 탐색했을 경우 방문하는 좌표 순서