[알고리즘] Leetcode_46_Permutations 순열

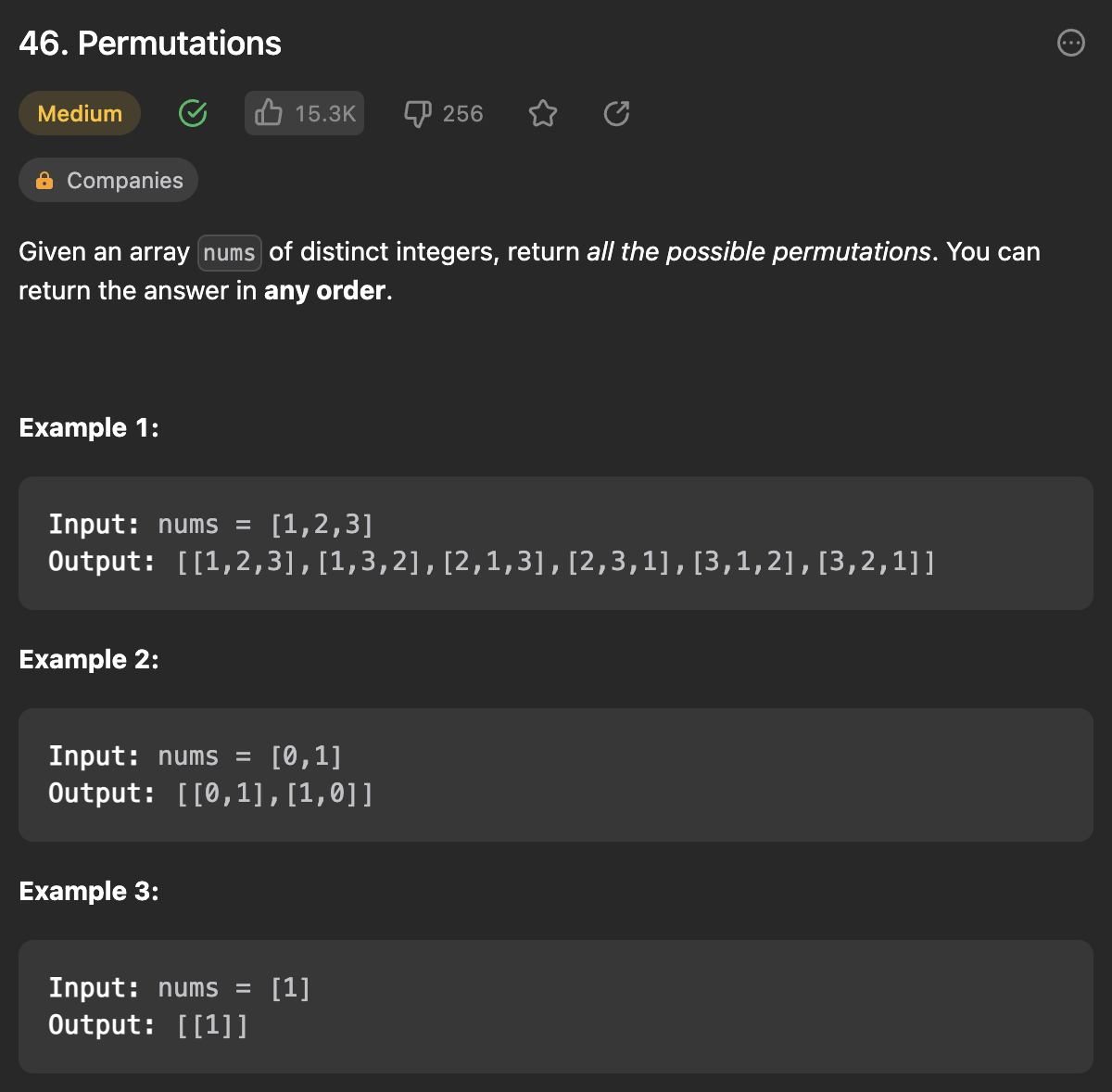
Problem

Solve

class Solution {
    public List<List<Integer>> answer = new ArrayList<>();
    public List<Integer> list = new ArrayList<>();

    public void permutation(int[] nums, int[] out, boolean[] visited, int depth){
        if(depth == nums.length){
            for(int num : out) list.add(num);
            answer.add(list);
            list = new ArrayList<>();
            return;
        }
        for(int i = 0 ; i < nums.length; i++){
            if(!visited[i]){
                visited[i] = true;
                out[depth] = nums[i];
                permutation(nums, out, visited, depth+1);
                visited[i] = false;
            }
        }
    }
    public List<List<Integer>> permute(int[] nums) {
        boolean[] visited = new boolean[nums.length];
        
        permutation(nums, new int[nums.length], visited, 0);
        return answer;
    }
}

Permutation 순열

서로 다른 n 개 중 순서있게 r 개를 뽑은 것

• [1,2] 와 [2,1] 는 순서가 다르기 때문에 순열의 경우의 수에 모두 포함이 된다.
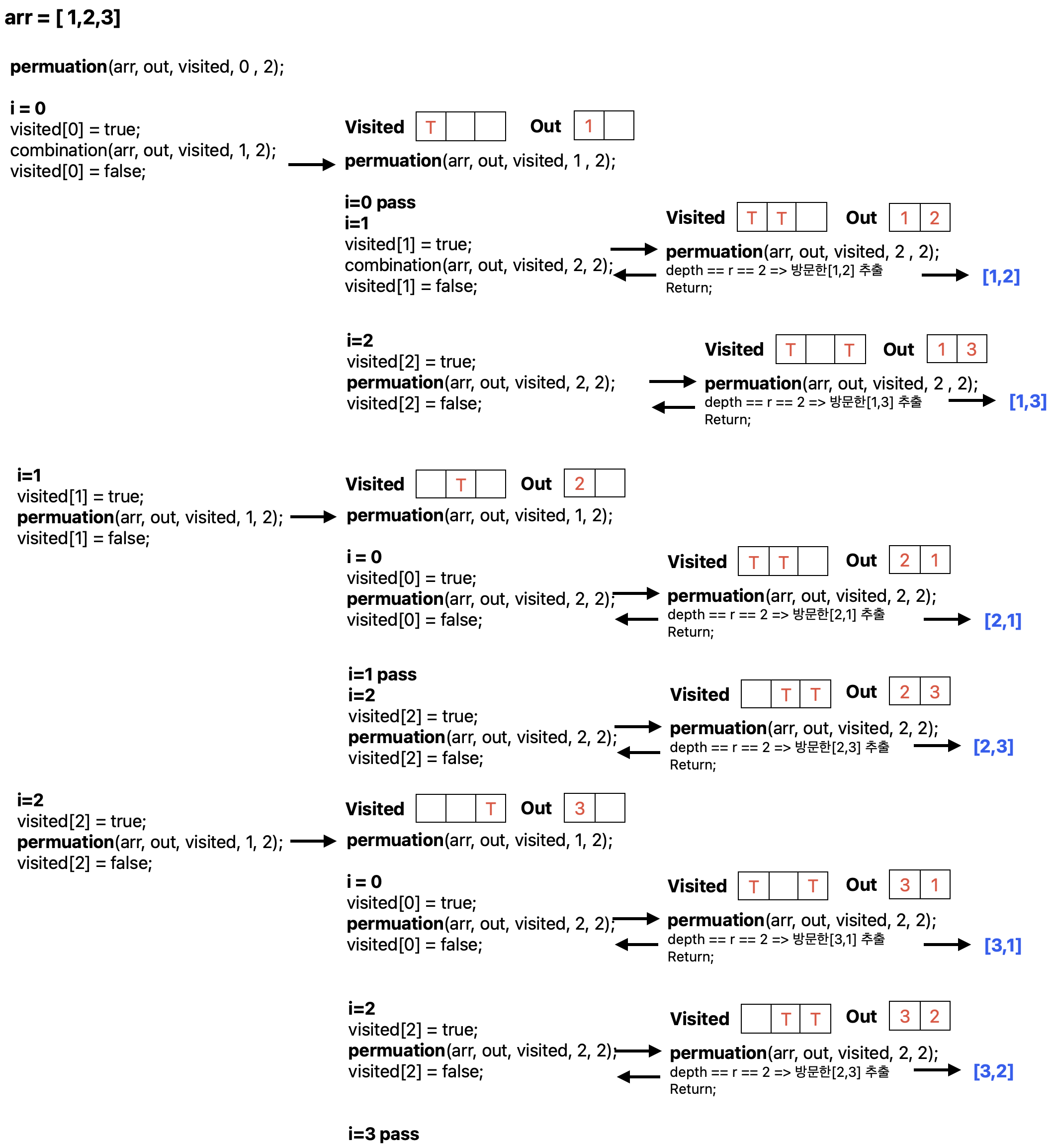
• 순서가 다르기 때문에 현재 원소보다 앞선 원소도 다 순회하여야 한다. 그래서 start 인덱스를 파라미터로 전달할 필요없이 for문에서 항상 첫번째부터 탐색하되 방문하지 않은 인덱스를 방문한 순서대로 out 배열에 원소 값을 할당하고 재귀를 호출한다.

public void permutation(int[] arr, int[] out, boolean[] visited, int depth, int r){
	if(depth == r) {
    	for(int num : out) System.out.println(num);
       	return;
    }
    
    for(int i = 0 ; i < arr.length ; i++){
    	if(!visited[i]){
			visited[i] = true;
            out[depth] = arr[i];
            permutation(arr, out, visited, depth+1, r);
            //첫번째 원소부터 탐색
            visited[i] = false;
        }
    }
}

arr = [1,2,3,4]
//2개 조합
[1,2]
[1,3]
[1,4]
[2,1]
[2,3]
[2,4]
[3,1]
[3,2]
[3,4]
[4,1]
[4,2]
[4,3]
=> 12가지

중복 순열

서로 다른 n 개 중 순서있고, 중복을 포함하는 r개를 뽑은 것

• 앞선 순열과 비슷하지만, 중복을 허용한다는 점에서 방문여부를 체크하는 visited 배열은 필요가 없다.

public void permutationWithDuplication(int[] arr, int[] out, int depth, int r){
	if(depth == r) {
    	for(int num : out) System.out.println(num);
       	return;
    }
    
    for(int i = 0 ; i < arr.length ; i++){
            out[depth] = arr[i];
            permutationWithDuplication(arr, out, depth+1, r);
            //첫번째 원소부터 탐색
        }
    }
}

arr = [1,2,3,4]
//중복 순열 2개 뽑기
[1,1]
[1,2]
[1,3]
[1,4]
[2,1]
[2,2]
[2,3]
[2,4]
[3,1]
[3,2]
[3,3]
[3,4]
=> 16가지