★★★★☆
알고리즘을 짜는건 어렵지않았지만 메모리 초과를 처리하는게 어려웠다..
개념
이분그래프는 그래프들의 정점의 집합을 서로 인접하지 않게 분할할 수 있는 그래프이다.
무슨 뜻이냐면, 2개의 색으로 그래프를 색칠할 때, 모든 정점들이 인접하는 정점과 다른 색을 가지고 칠해지는 것이다. (고등학교에서 확률 시간에 많이 봤던 느낌)
나의 풀이
-
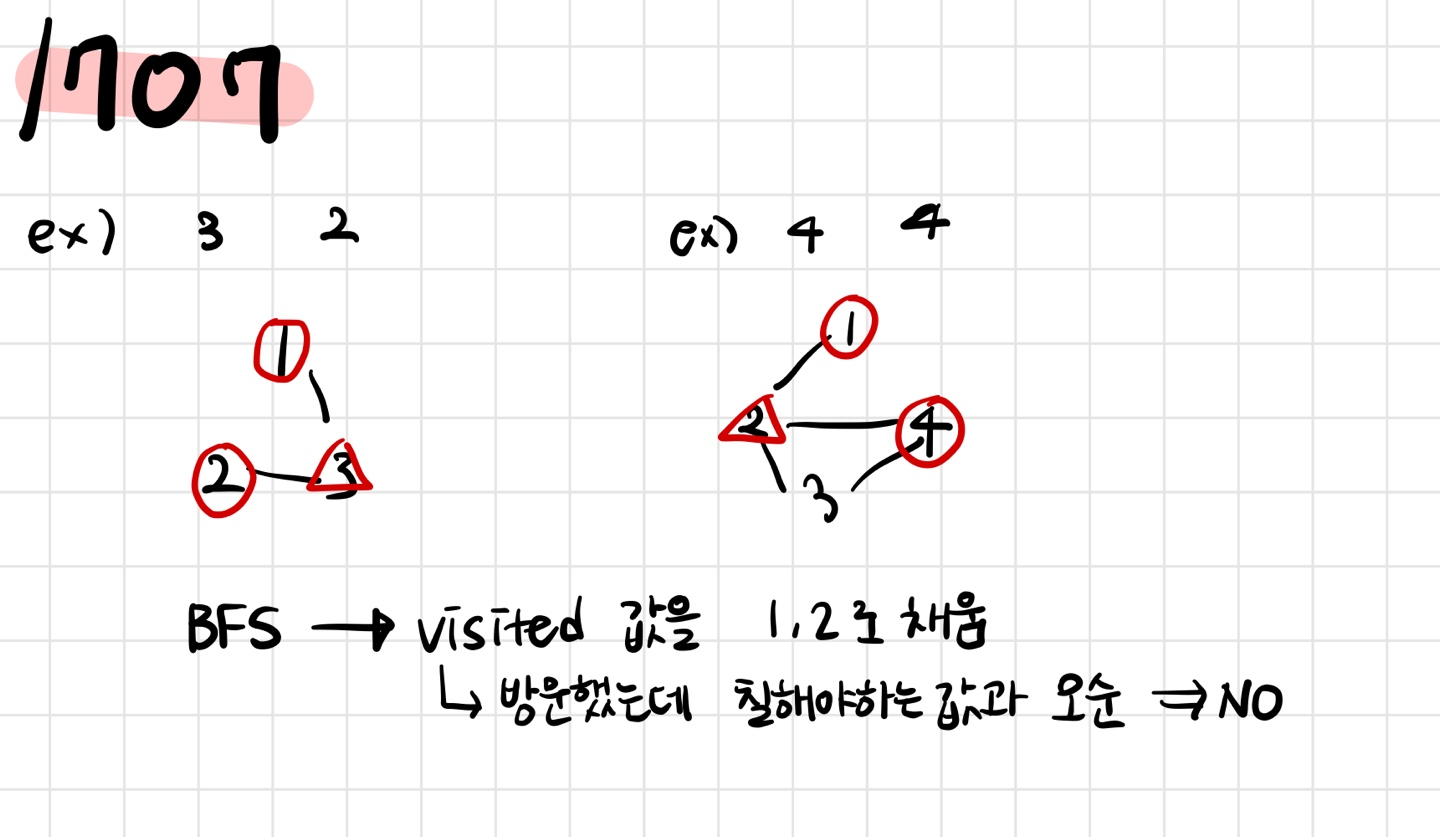
이번 문제는 BFS를 가지고 풀이하기로 했다. '인접한' 정점들의 색을 칠하게 되기때문에,
한 정점을 중심으로 인접한 정점들에 접근하는 BFS가 더 적합하다고 생각했다. -
visited의 값을 이전에는 bool 값으로 사용했지만, 이번에는 어떤 값이 채워져있는지를 알기 위해 int 배열로 선언하고,
채워진 값들을 비교해 인접한 정점끼리의 값이 같다면 이분 그래프가 아니다! 라는 결론을 내도록 했다. -
1회 결과를 내는 것은 비교적 쉬웠으나, 메모리를 처리하는 것이 어려웠다..
기존에는 2차원배열을 이용하여 구현하였는데, 이번에는 정점의 최댓값이 증가하여
무려 20000*20000 사이즈의 배열을 만들었어야 했으므로 메모리초과가 날 수밖에 없었다.
=> graph를 vector 배열로 수정해주었다. -
k번의 실행을 하는 동안, 초기에는 제대로된 값들이 나오다가 후반으로 갈수록 이상한 값들이 나왔는데, visited 배열과 graph 배열을 초기화해주지 않았기 때문이었다.
=> 초기화 함수 추가 -
매 실행마다 graph를 초기화해주는 과정에서, 기존에는 2중 for문을 사용하여 모든 정점 값을 초기화해주어야 했다면, 이제는 graph[i] 벡터를 clear해주기만 하면 되었다.
BFS에 대한 이해와 메모리에 대한 이해를 늘리기 위해서라도 다음에 다시 풀어봐야할 문제이다.
#include <iostream>
#include <queue>
#define MAX 20001
using namespace std;
int v, e;
vector<int> graph[MAX]; //벡터 배열
int visited[MAX]; //0,1,2 번갈아가면서 채워줄것
queue<int> q;
void init() { //배열을 초기화해주는 함수
for (int i = 0; i <=v; i++) {
visited[i] = 0;
graph[i].clear();
}
}
void bfs(int start, int tile) { //번갈아가면서 타일을 채움
q.push(start);
visited[start] = tile;
//cout << start << "\n";
//cout << "정점 " << start << " , " << visited[start] << " 채움 \n";
while (!q.empty()) {
int tem = q.front();
q.pop();
if (visited[tem] == 1) tile = 2; //현재 타일과 색이 겹치지 않도록, 칠해줄 색을 변경해줌
else if (visited[tem] == 2) tile = 1;
for (int i = 0; i <graph[tem].size(); i++) {
if (visited[graph[tem][i]] == 0) {
visited[graph[tem][i]] = tile;
q.push(graph[tem][i]);
//cout << "정점 " << graph[tem][i] << " , " << visited[graph[tem][i]] << " 채움 \n";
}
}
}
return;
}
int isBipartiete() { //이분그래프인지 확인하는 함수
for (int i = 1; i <= v; i++) {
for (int j = 0; j < graph[i].size(); j++) {
if (visited[i] == visited[graph[i][j]]) { //인접한 정점과 같은 값이라면
return -1; //이분 그래프가 아님
}
}
}
return 0;
}
int main() {
int k;
cin >> k;
while (k > 0) {
//cout << "\n\ncase " << 11-k << " ==========================\n";
cin >> v >> e;
for (int i = 0; i < e; i++) {
int x, y;
cin >> x >> y;
graph[x].push_back(y);
graph[y].push_back(x);
}
for (int i = 1; i <= v; i++) {
if (visited[i] == 0) {
bfs(i, 1); //기본 타일값을 1로 설정하여 bfs 진행
}
}
if (isBipartiete() == -1) cout << "NO\n";
else cout << "YES\n";
init(); //벡터와 배열 초기화
k--;
}
}참고
이분 그래프 개념
https://woovictory.github.io/2020/01/26/Bipartite-Graph/
반례, 벡터배열 사용
https://jdselectron.tistory.com/51
