백준 2133

★★★☆☆

지난 번의 2*n 타일링 문제를 변형한 문제
풀었던 기억을 상기시키면서 코드를 작성했더니
뭔가 허무하게? 정답처리가 되었다

<나의 풀이>

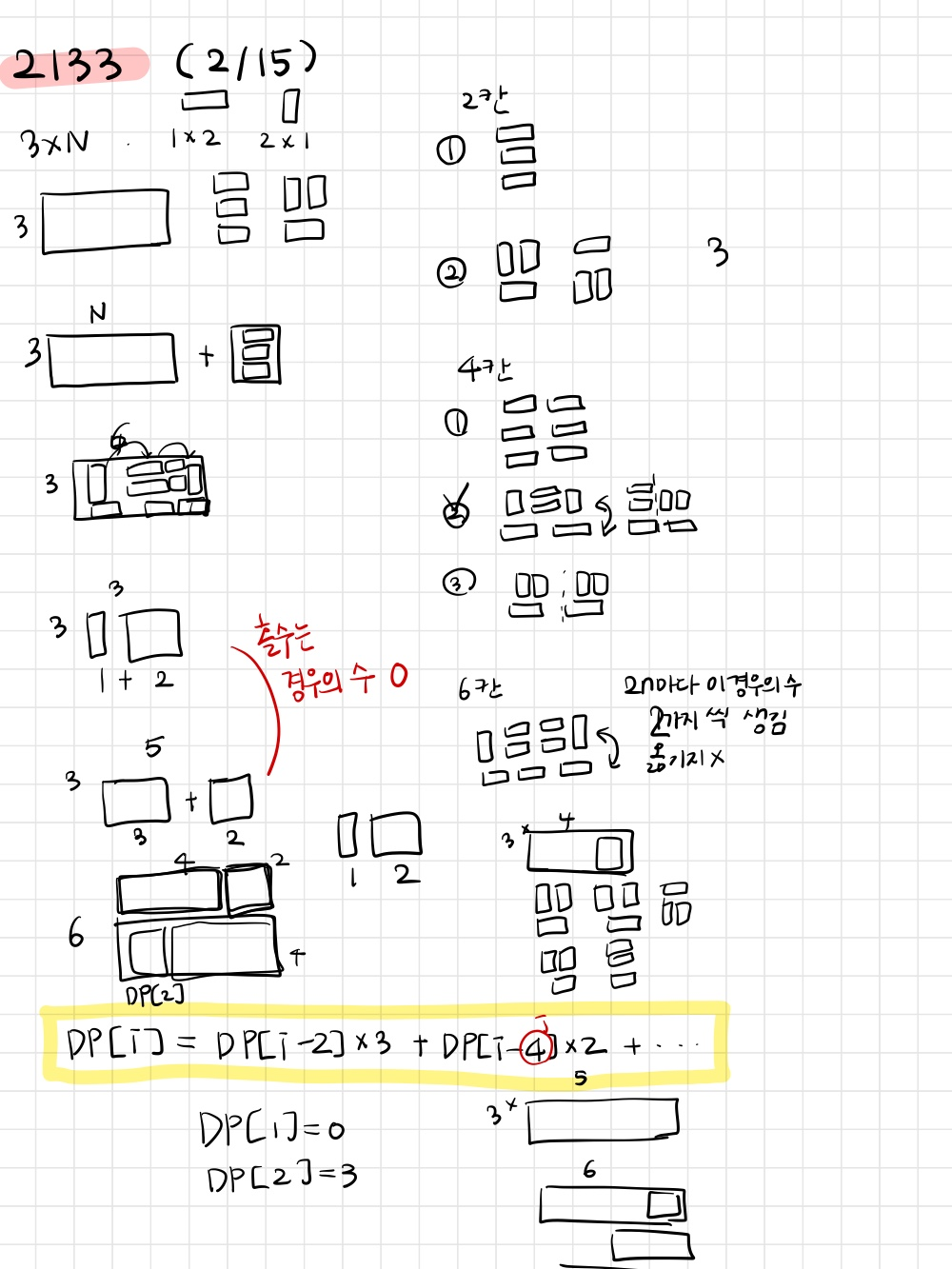
일단 처음에 감을 못잡아서 6까지는 직접 어느정도 구해보았다.
그 결과 홀수는 경우의 수가 없다는 것,
2칸, 4칸, 6칸으로 고정된 모양의 결과가 나온다는 것을 알 수 있었다. (상하 반전된 모습으로!)
이때, 괜히 4칸의 경우에서 옮기는 것까지 생각하면 중복도 발생하기때문에..고정한다는 의미로 생각하는게 더 좋다

즉, 3i의 타일은 2칸, 4칸, 6칸으로 끝을 잘라내면서 나머지 칸의 경우의수들과 곱해주면 된다.
**dp[i]=dp[i-2]3+dp[i-4]2+dp[i-6]2+... **

이 점화식에서 i-2, i-4, i-6을 만들어내기 위해 j를 변수로하는 for문을 사용해주었다.

<다른 사람의 풀이>

다른 사람의 코드를 참조한 결과, 기본 알고리즘은 동일하지만
for문을 한 개만 사용하는 코드를 발견했다.
dp[i]+=dp[n-i]*2 ? 의 점화식을 사용한다.
이 문제에서는 n의 범위가 30까지이기 때문에 큰 문제가 없었지만, n이 100000까지 가던 다른 문제들을 고려한다면 j를 사용하지 않고 for문을 한 개만 사용하는 것을 지향해야겠다.

https://github.com/jeongopo/DaliyCodeCpp/commit/968192a90e6ef14e03a6c077e999c90c9fe61b11