백준 2609 : 최대공약수와 최소공배수

★★★☆☆

그냥 약수들을 계속 나누어서 구하면 간단하게 풀 수 있는데,
숫자가 커지는 경우와 효율성을 고려하여 유클리드 호제법을 사용하려고 하니까 어려웠다.

<나의 풀이>

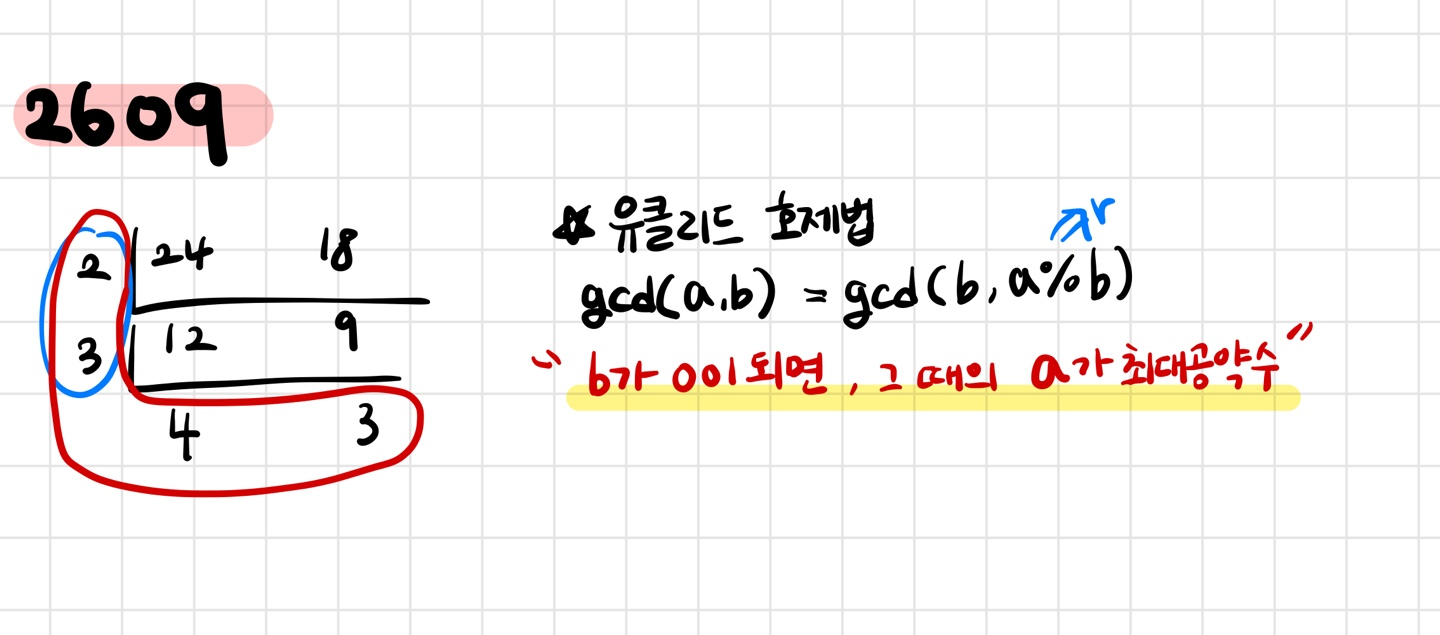
유클리드 호제법에 따르면,
a와 b의 gcd(최대공약수)는 b와 a%b 사이의 최대공약수와 같다.
(증명을 열심히 봤지만 이해하기 어려웠다..)

따라서 반복문에 a%b의 값을 계속해서 정의하고,
a%b가 0이 될 때, 그 때의 a 값이 최대공약수가 된다.

최소공배수최대공약수=ab이므로
최소공배수는 a*b를 최대공약수로 나눈 값과 같다.

#include <iostream>

using namespace std; 
int gcd(int a, int b) { 
	int r; 
	while (b != 0) { 
		r = a % b; 
		a = b; 
		b = r; 
	} 
	return a; 
} 
int main() {
	int a, b;
	cin >> a >> b;

	cout << gcd(a, b) << "\n";
	cout << (a * b) / gcd(a, b) << "\n";
	return 0;
}

<다른 사람의 풀이>

재귀함수를 통해 gcd 함수를 구현할 수 있다.
그러나 재귀함수는 오류가 많아 잘 사용하지는 않는다는 것 같다.

참고

https://fjvbn2003.tistory.com/37