튜링머신

Jeongtae Kim·2024년 3월 11일

youtube의 TMItalk. 튜링 머신의 이해 를 보고 정리한 글 입니다.

AI 3줄 요약

힐베르트의 꿈, 즉 모든 수학적 명제를 도출하는 만능기계의 생각은 괴델의 불완전성 정리에 의해 불가능함이 증명되었으며, 이어서 튜링이 정지 문제를 제기하여 '모든 수학적 명제를 도출하는 기계'가 가능하지 않음을 더욱 강조하였습니다.

이러한 과정을 통해 '모든 수학적 명제를 도출하는 기계'는 발전하여 튜링머신을 완성하였고, 이 튜링머신은 현재의 컴퓨터 발전의 기반이 되었습니다.

튜링머신은 테이프, 헤드, 기호 집합, 상태 집합의 네 가지 구조로 이루어져 있으며, 이를 Python으로 간단하게 구현한 예제도 제시되었습니다.

튜링머신 발전 순서

힐베르트의 꿈

다비트 힐베르트 (20세기 수학자)가 낸 힐베르트 문제 중 하나

정의와 공리를 입력하면 모든 수학적 명제를 도출해 줄 수 있는 만능기계가 있으면 좋겠다 라고 생각함
이 문제를 해결하기 위해 많은 수학자가 도전

불완전성 정리 (쿠르트 괴델)

페아노 공리계를 포함한 모든 무모순적 공리계는 참인 일부 명제를 증명할 수 없다.
위 정리로 힐베르트 문제는 불가능 하다는 것으로 종료됨.
불완전성 정리
불완전성 정리 나무위키 페이지

제1정리. 페아노 공리계를 포함하는 어떠한 공리계도 무모순인 동시에 완전할 수 없다. 즉 자연수 체계를 포함하는 어떤 체계가 무모순이라면, 그 체계에서는 참이면서도 증명할 수 없는 명제가 적어도 하나 이상 존재한다.
제2정리. 페아노 공리계가 포함된 어떠한 공리계가 무모순일 경우, 그 공리계로부터 그 공리계 자신의 무모순성을 도출할 수 없다.

정지 문제 (앨런 튜링)

힐베르트의 꿈 문제대로 모든 수학적 명제를 도출하는 기계를 설계한 뒤 풀 수 있는 모든 문제를 푼다.
그 기계로 풀수 없는 문제가 정지 문제 (괴델의 불완정성 정리와 비슷한 내용)
모든 수학적 명제를 도출하는 기계 ⇒ 튜링머신 ⇒ 컴퓨터 의 순서로 발전하게 된 것

튜링머신

구조

테이프
- 기호 하나를 읽고 쓸 수 있는 셀이 무한히 연결된 기억 장치
- 저장장치, 현재의 메모리 역할
헤드
- 현재 위치한 셀을 읽고 쓰거나 좌우로 이동할 수 있는 제어 장치
- 현재의 CPU 역할
기호 집합
- 테이프에 읽고 쓸 수 있는 기호들의 집합
- 정보 (숫자, 문자, 등 …)
상태 집합
- 튜링 머신이 가질 수 있는 상태들의 집합 $s_1, s_2, s_3, ...$

Turing Maching 구현 (Python)

Run Python in the browser - glot.io 에서 돌려보시면 편리합니다.

code

class Tape:
    def __init__(self, *, debug: bool=False):
        self._tape = [0 for _ in range(2**4)] # 테이프의 길이는 무한하다고 가정
        self._idx = 2**4 // 2 # 인덱스
        self._status = 0
        self._debug = debug
        
    def __str__(self) -> None:
        return str(self._tape)
        
    def read(self) -> int:
        return self._status, self._tape[self._idx]
        
    def set_tape(self, n: int, move_idx: int, status: int) -> None:
        self._tape[self._idx] = n
        self._idx += move_idx
        self._status = status
        
        if self._debug:
            print(str(self._tape))
        

class Head:
    
    def __init__(self, tape: Tape, lines: list):
        self._tape = tape
        self._commands = [list(map(int, line.split(","))) for line in lines]
        
    def action(self) -> bool:
        status, value = self._tape.read()
        
        if status == -1:
            return False
        
        for idx, command in enumerate(self._commands):
            if command[0] == status and command[1] == value:
                break
            
        command = self._commands[idx]
        self._tape.set_tape(command[2], command[3], command[4])
        
        if command[4] == -1:
            return False
        
        return True

if __name__ == "__main__": 
    lines = list()
    for _ in range(int(input())):
        lines.append(input())
    
    tape = Tape(debug=True)
    head = Head(tape, lines)
    
    c = True
    while c:
        c = head.action()
    
    print(f"result: {tape}")

input

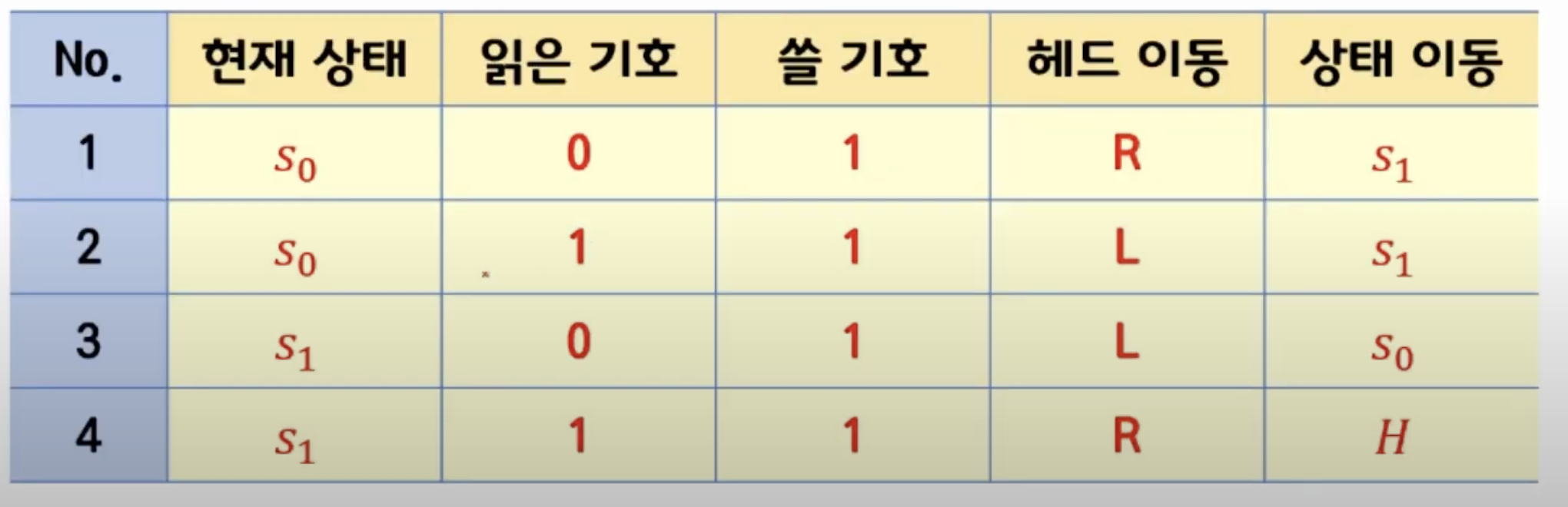
4
0,0,1,1,1
0,1,1,-1,1
1,0,1,-1,0
1,1,1,1,-1

output

[0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0]
result: [0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0]