1. 평균값 필터링의 단점

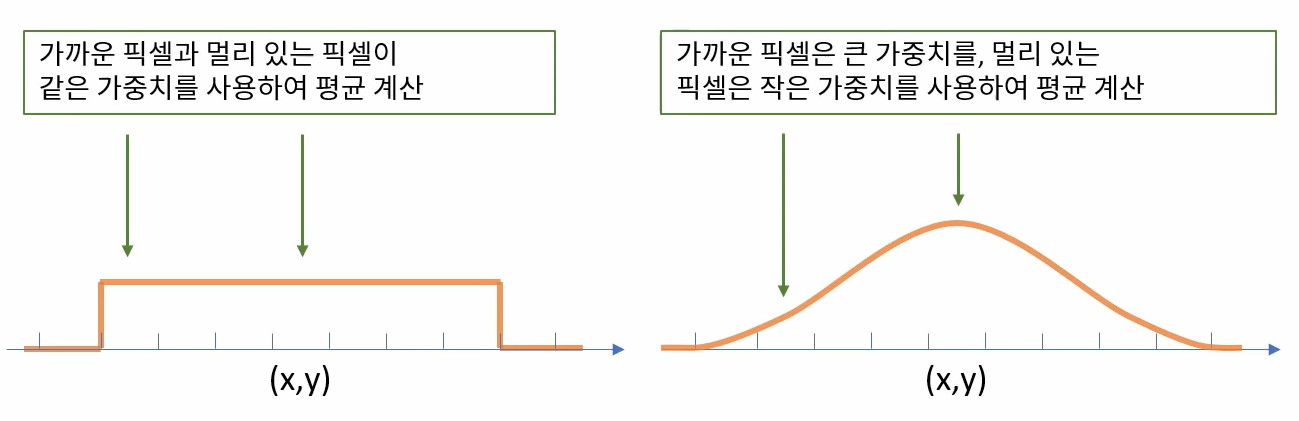
• 필터링 대상 위치에서 가까이 있는 픽셀과 멀리 있는 픽셀이 모두 같은 가중치를 사용하여 평균을 계산
• 멀리있는 픽셀의 영향을 많이 받을 수 있음
• 가우시안 필터는 멀리 있는 픽셀들의 영향이 적음
  

2. 정규분포와 가우시안 함수

정규분포란?

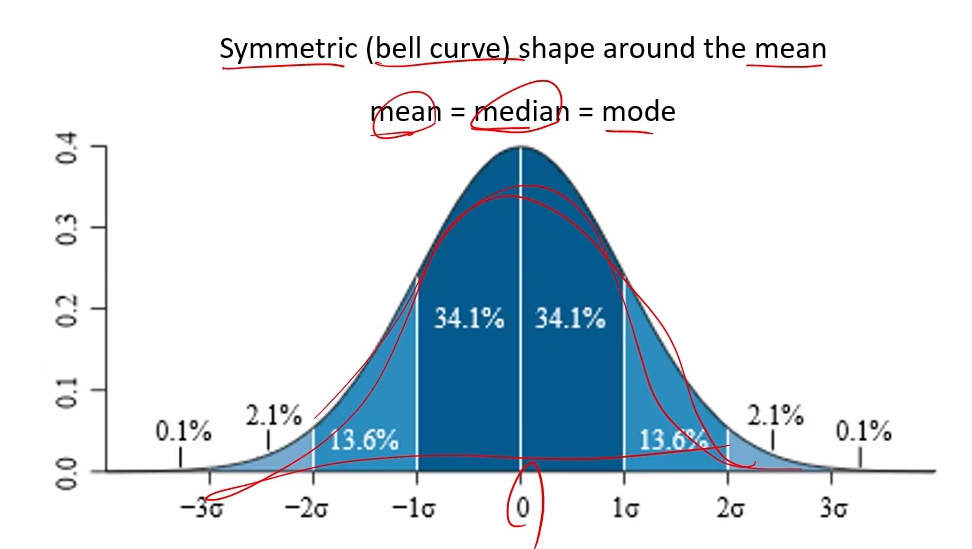
• 평균을 중심으로 좌우대칭인 종 모양을 갖는 확률분포
• 가우시안 분포
• 자연계에서 일어나는 수많은 일을 설명할 수 있음
• 키, 몸무게, 시험점수, 잡음, 측정오차, 제품수명 등

1차원 가우시안 함수

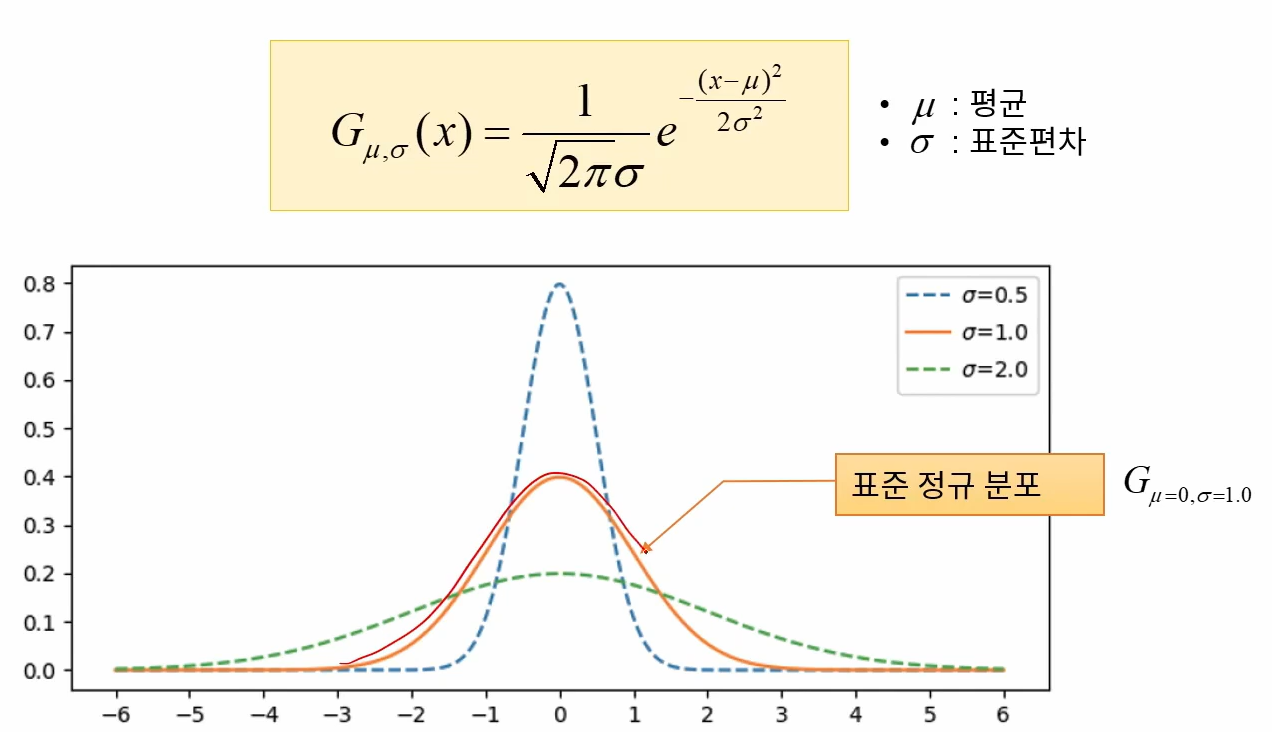
가우시안 함수의 특징

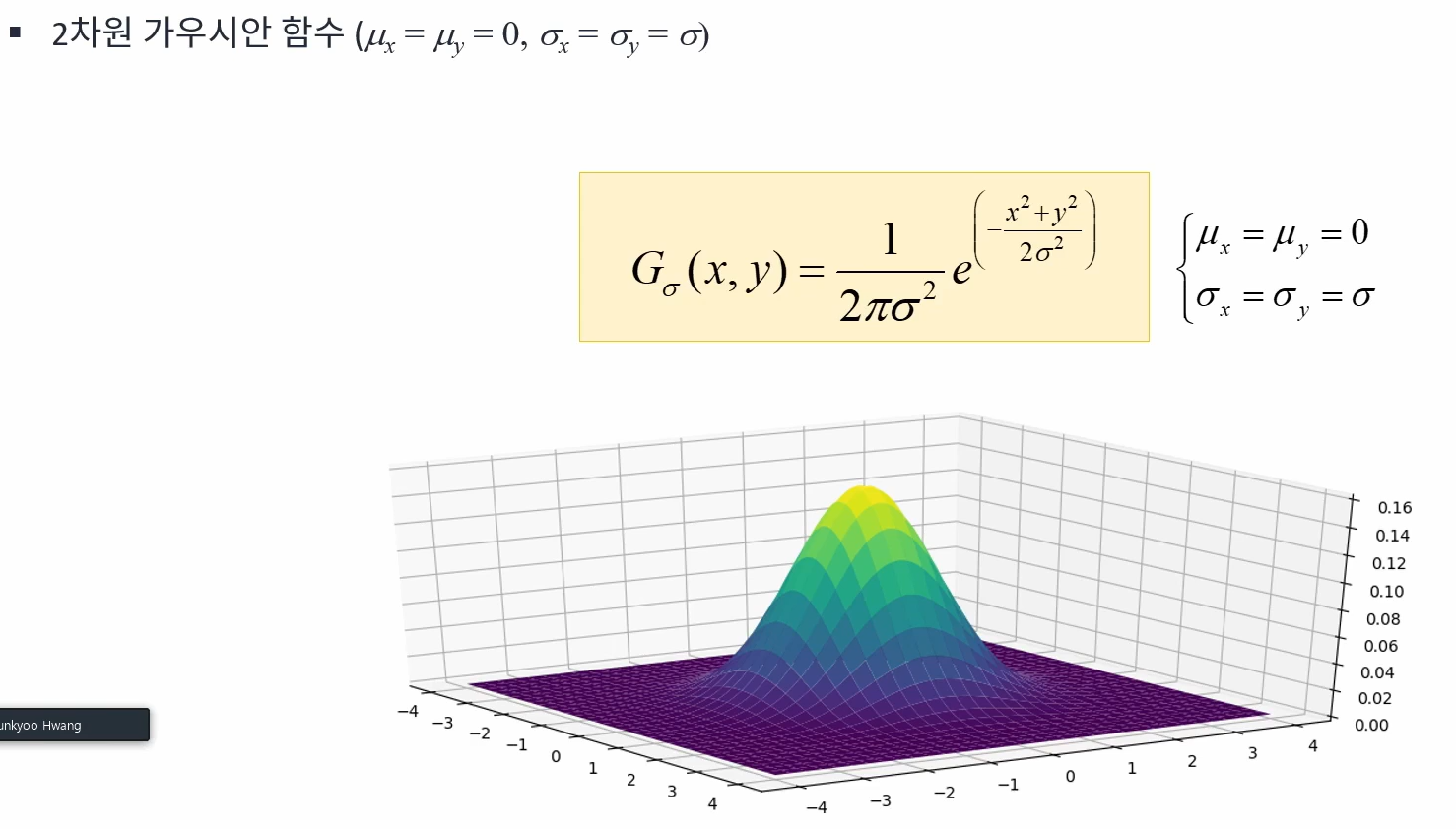
2차원 가우시안 함수

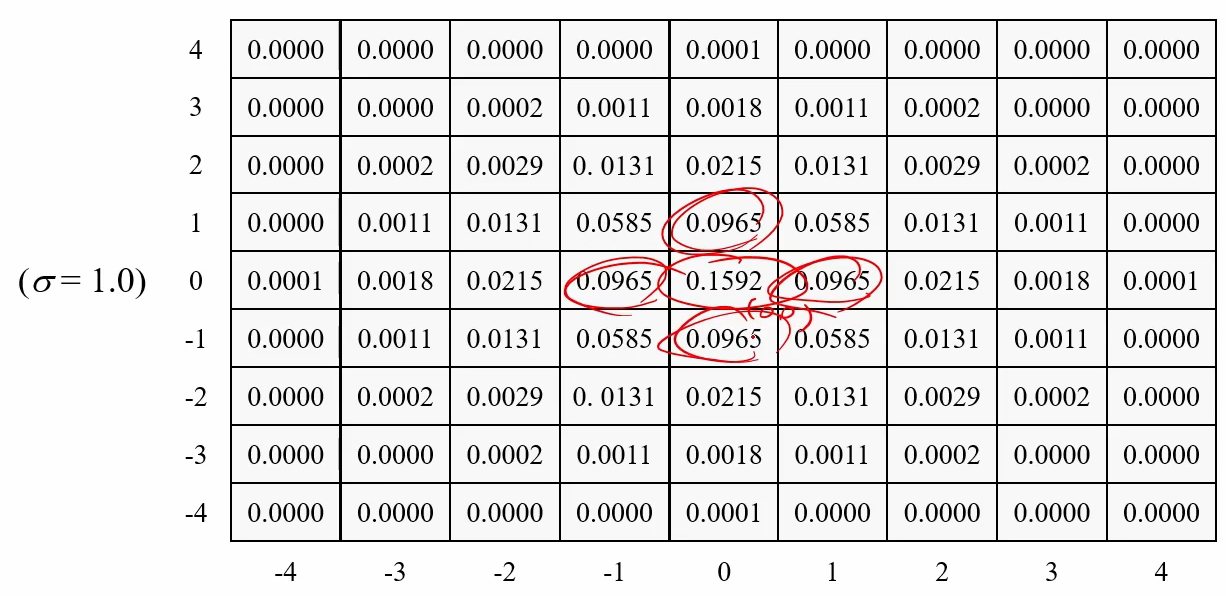
2차원 가우시안 필터의 마스크

• 필터마스크 크기: 8a+1 or 6a+1

OpenCV 1차원 가우시안 필터 마스크 구하기

Mat getGaussianKernel(int ksize, double sigma, int ktype = CV_64F);

• ksize: 커널크기. 0보다 큰 홀수.
• sigma: 표준편차. 만약 sigma 값이 음수이면 sigma=0.3((ksize-1)0.5 - 1) + 0.8형태로 자동계산된다.
• ktype: 커널 타입. CV_32F 또는 CV_64F.
• 반환값: ksize x 1 크기의 가우시안 필터 마스크. 원소 전체의 합이 1이 되도록 정규화를 수행.

void GaussianBlur(InputArray src, OutputArray dst, Size ksize, double sigmaX, double sigmaY = 0, int borderType = BORDER_DEFAULT);

• src: 입력영상. 각 채널별로 처리됨
• dst: 출력영상. src와 같은 크기, 같은 타입.
• ksize: 가우시안 커널크기. Size()를 지정하면 sigma 값에 의해 자동결정됨.
• sigmaX: x방향 sigma.
• sigmaY: y방향 sigma. 0이면 sigmaX와 같게 설정.
• borderType: 가장자리 픽셀 처리방식.

실습코드

int main() {
	Mat src = imread("baduk.png", IMREAD_GRAYSCALE);
    Mat dst1, dst2;
    
    blur(src, dst1, Size(9,9));
    
    GaussianBlur(src, dst2, Size(), 3);
    
    imshow("src", src);
    imshow("dst1", dst1);
    imshow("dst2", dst2);
    
    waitKey();  

}

결과영상

가우시안블러를 했을 때 일반 블러보다 바둑판 선이 더 선명했다.
멀리있는 픽셀의 영향을 가까이 있는 픽셀들 보다 적게 받았다는 것을 의미한다.