TIL 221110

1. 정렬

이론은 이해가 가는데, 직접 코드를 작성하는데서 계속 버벅여서 다시 듣고 정리한다.

1) bubble sort

가장 기본적인 정렬
각각의 인덱스를 반복하면서, 현재와 뒤의 수를 비교하고 정렬한다.
3 5 7 1 2 라는 수가 있으면

1단계
3    5    7    1    2 
i   i+1
# 현재수와 다음 수를 비교했을 때 현재수가 작으므로 그대로

2단계
3    5    7    1    2 
     i   i+1
# 1단계와 마찬가지

3단계
3    5    7    1    2 
          i   i+1
# 현재수와 다음수를 비교했을 때 현재수가 더 크므로
3    5    1    7    2
# 위와 같이 변경

4단계
3    5    1    7    2
               i   i+1
# 3단계와 동일
3    5    1    2    7

#위 4단계를 반복(j)한다, 하지만 마지막 수는 정렬되어 있으므로 4단계는 생략

코드로 표현하면 아래와 같다

#py
def bubble_sort(array):
    for i in range(len(array)-1): # array의 길이보다 1 짧게 비교를 실행
        for j in range(len(array)-1-i) # 마지막으로부터 i만큼의 수는 정렬되어 있기 때문에 이렇게 비교 실행
            if array[j] > array[j+1]: # 현재수가 다음수보다 크면,
                array[j], array[j+1] = array[j+1], array[j] # 서로 대치
    return array

2중반복문이므로 T(n)=O(N^2)의 시간복잡도를 가진다.

2) Selection Sort

들어갈 인덱스를 정해놓고, 인덱스에 들어갈 원소를 선택해서 정렬하는 정렬방법.
(정의를 적어보니 이해가 한결 쉬워지는거 같다.)

1단계
  3    5    7    1    2 
index         (최솟값)
  1    5    7    3    2 
# 최솟값인 1을찾아 현재 정해놓은 index와 변경

2단계 #index(0을 제외하고 탐색)
  1    5    7    3    2 
     index         (최솟값)
  1    2    7    3    5 

3단계 #index(0,1을 제외하고 탐색)
  1    2    7    3    5 
         index(최솟값)
  1    2    3    7    5 

...

  1    2    3    5    7 

코드로 표현하면

def selection_sort(array):
    for i in range(len(array)-1):
        min_idx = i
        for j in range(len(array)-i):
            if array[i+j] < array[min_idx]:
                min_idx = i+j
        
        array[i], array[min_idx] = array[min_idx], array[i]
    return array

Bubble Sort와 마찬가지로 T(n)=O(N^2)의 시간복잡도를 가진다.

3) insertion sort

각 원소를 정렬된 곳에 자리를 찾아 앞쪽부터 정렬한다.

1단계
<---- # 정렬 된 부분
  3    5    7    1    2 
    index
# 정렬 된 부분에 index보다 큰 값이 없으므로 제자리

2단계
<---------- # 정렬 된 부분
  3    5    7    1    2 
    	  index
          
3단계
<--------------- # 정렬 된 부분
  3    5    7    1    2 
    	       index
#index가 3보다 작으므로 정렬
  1    3    5    7    2
  
4단계
3단계
<-------------------- # 정렬 된 부분
  1    3    5    7    2
    	            index
#index가 3보다 작으므로 정렬
  1    2    3    5    7

코드로 표현하면

def insertion_sort(array):
    for i in range(1, len(array)):
        for j in range(i,0,-1):
            if array[j-1] > array[j]:
                array[j-1],array[j]=array[j],array[j-1]
    return array

만약 정렬되어있는 상태의 배열이라면 T(n) = O(N)만큼의 시간복잡도를 가지게 되지만, 최악의 경우는 T(n) = O(N^2)만큼의 시간복잡도를 가지게 된다.

4) merge sort

각 배열을 쪼갠다음 다시 합치면서 정렬하는 형태
merge sort는 3단계로 작동된다

• 분할 : input 배열을 같은 크기의 2개의 부분 배열로 만든다.
• 정복 : 부분 배열을 정렬한다. 만약 부분 배열의 크기가 충분히 작지 않으면 다시 분할 정복 방법을 적용한다.
• 결합 : 정복된 부분 배열들을 하나의 배열에 합병한다.

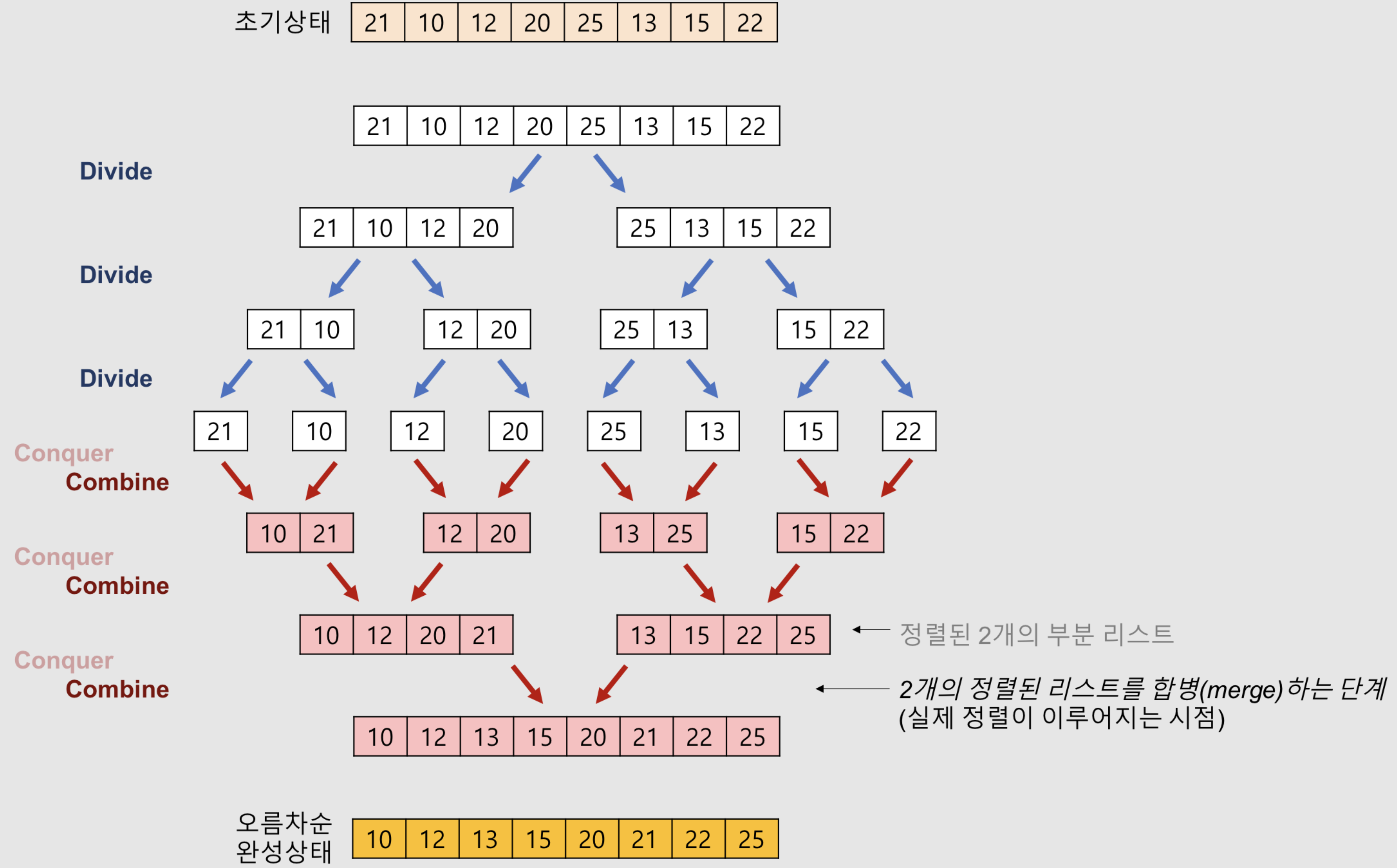
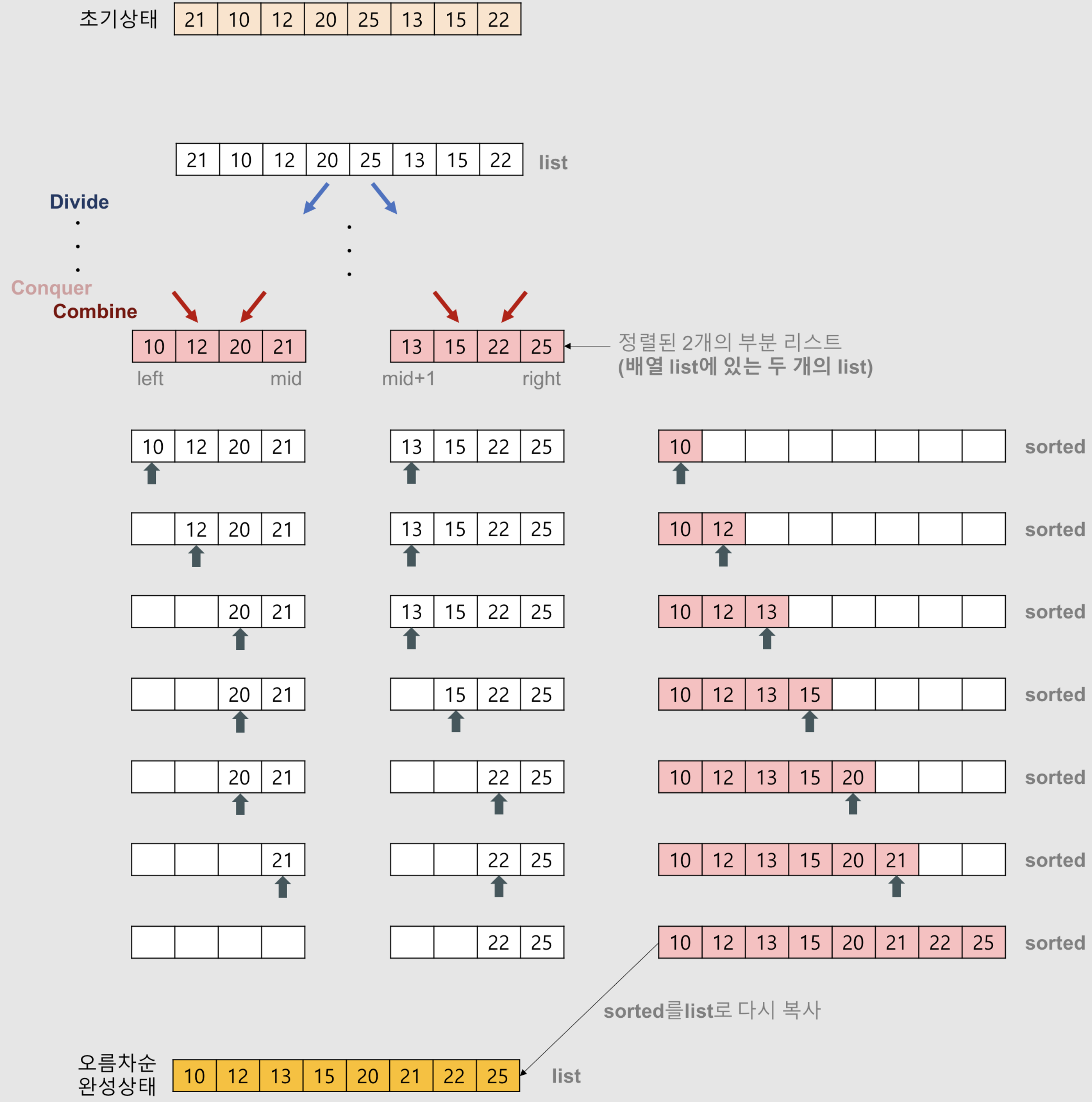
사진출처 : https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html

코드 구현을 2단계에 나눠서 진행하면
I) 결합단계

def merge(array1, array2):
    result = []
    # len(array1) len(array2) 둘 다 존재할 때
    while len(array1) != 0 and len(array2) != 0 :
        if array1[0] < array2[0]:
            result.append(array1.pop(0))
        else:
            result.append(array2.pop(0))

    # 위 while을 실행하고 array1이 남아있을 때
    while len(array1) != 0 :
        result.append(array1.pop(0))
        
    # 위 while을 실행하고 array2가 남아있을 때
    while len(array2) != 0 :
        result.append(array2.pop(0))
    
    return result

II)분할 및 정복 단계

def merge_sort(array):
	#더이상 array를 분할할 수 없을 때 array를 return
    if len(array) <= 1:
        return array
    mid = (0+len(array)) // 2
    array1 = array[:mid]
    array2 = array[mid:]
    return merge(merge_sort(array1), merge_sort(array2))

T(n)=O(NlogN)의 시간복잡도를 가진다.

2. split(" ") | split()

1)두 명령의 차이점

split(" ")은 딱 스페이스바로 만든 공백만 인식해 잘라준다.(탭, \n 은 인식 못함)
또, 공백 뒤에 오는 공백은 객체로 인식해버린다
하지만 split()은 모든 공백을 처리하고 이어진 공백은 하나로 처리한다.

my_string = "a bb  ccc   dddd    "
my_string.split(" ") # ['a', 'bb', '', 'ccc', '', '', 'dddd', '', '', '', '']
my_string.split() # ['a', 'bb', 'ccc', 'dddd']