그래프란?

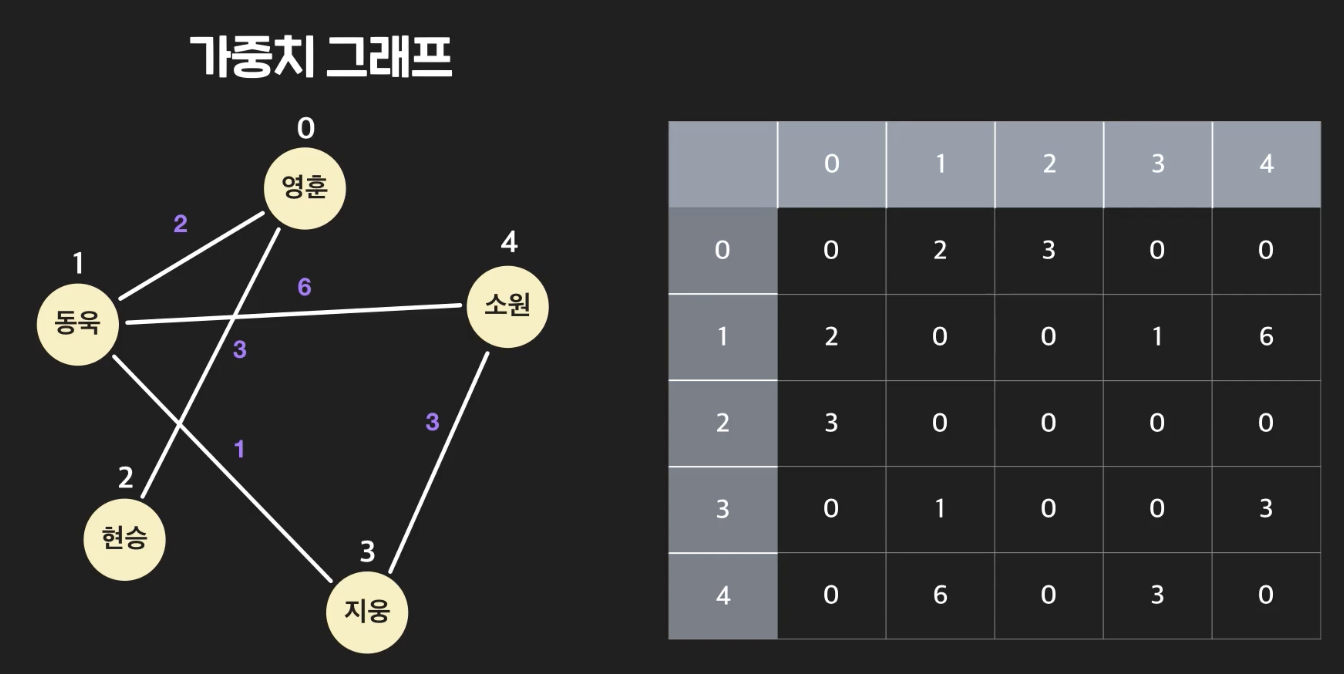
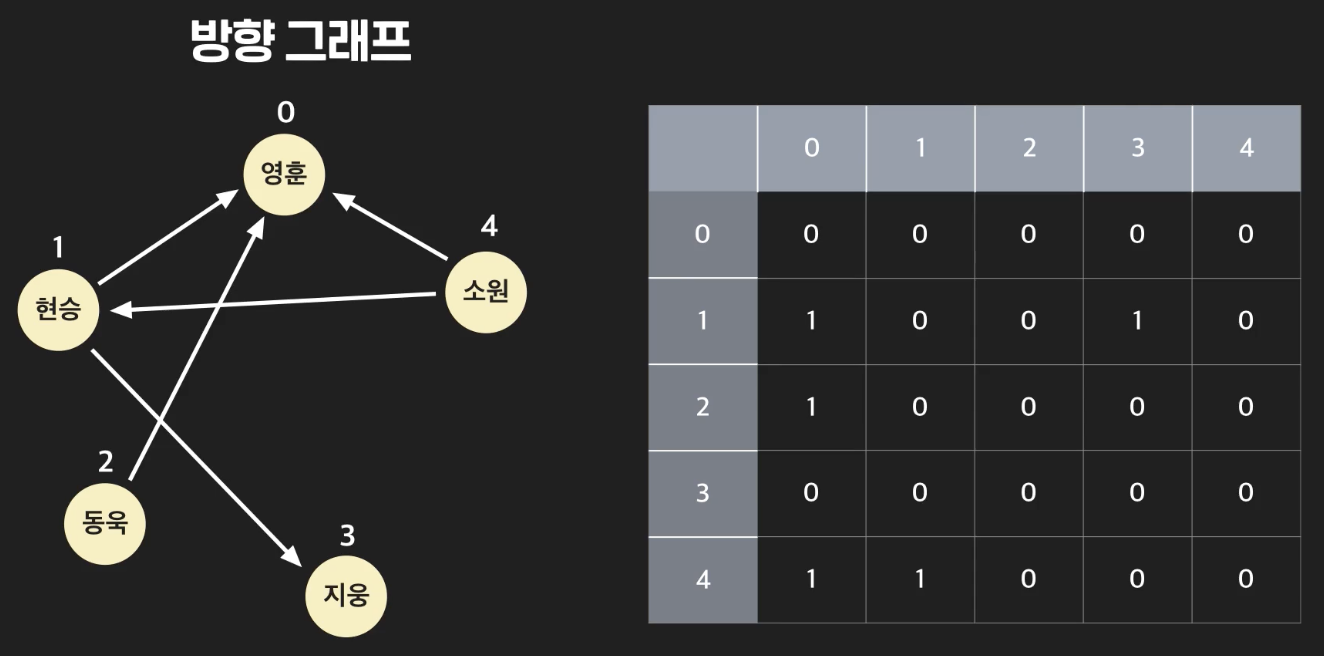
1. 연결 관계 데이터와 그래프

그래프(Graph)

• 유한하고 셀 수 있는 정점(verties)과 edges 또는 arcs로 구성된 자료 구조
• edge에 방향(reference)과 weight 값을 할당할 수 있다.

무방향 그래프(undirected graph)

• edge로 구성된 그래프
• edge는 방향성이 없다.

방향 그래프(directed graph)

• arc로 구성된 그래프
• arc는 방향성이 있다.
• 일방향 그래프, 쌍방향 그래프가 있다.

연결 관계 예시

• 위치 데이터 사이의 거리, 걸리는 시간
• 소셜 네트워크 데이터
• 수많은 컴퓨터들의 연결 관계인 인터넷
• 유전자와 단백질의 상호 작용 관계

2. 그래프 기본

• edge: 두 정점을 연결하는 선
• arc 방향성이 있는 edge
• loop: 정점 자기 자신을 연결하는 edge
• multiple edges: loop를 형성하는 edges
• simple graph: 두 정점 사이에 둘 이상의 edge가 없고, loop가 없는 그래프
• adjacaent vertices: edge/arc로 연결되어 있는 두 정점
• adjacent edges: 공통 정점을 공유하는 edges
• degree of a vertex: 해당 정점에 연결된 edges 수
• indegree of a vertex: 해당 정점에 연결된 들어오는 arc 수
• outdegree of a vertex: 해당 정점에 연결된 나가는 arc 수
• path: 인접한 정점들의 나열
• simple path: 중복된 정점이 없는 path
• circuit: 시작과 끝 점이 같은 path
• cycle: 중복되는 정점이 없는 circuit
• a connected graph: 임의의 서로 다른 두 정점이 연결된 그래프
• disconnected graph: 다른 정점과 연결되지 않은 정점이 있는 그래프
• components: disconnected graph를 구성하는 connected subgraphs
• weighted graph: edge에 weight가 있는 그래프
• Unweighted Graphs: edge에 weight가 없거나 weight가 모두 동일한 그래프
• distance of path: path에 있는 edges의 weight의 합. unweighted graph라면 모든 weight를 1로 계산한다.
• bridge: 삭제했을 때 components 갯수가 늘어나는 edge
• Euler path: connected graph의 모든 edges를 지나가는 path
• Euler circuit: connected grpah의 모든 edges를 지나가는 circuit

3. 그래프 노드 구현

class StationNode:
    """지하철 역 노드를 나타내는 클래스"""
    def __init__(self, name, num_exits):
        self.name = name
        self.num_exits = num_exits


station_0 = StationNode("교대역", 14)
station_1 = StationNode("사당역", 14)
station_2 = StationNode("종로3가역", 16)
station_3 = StationNode("서울역", 16)

# 노드들을 파이썬 리스트에 저장
# stations = [station_0, station_1, station_2, station_3]

# 노드들을 파이썬 딕셔너리에 저장
stations = {
    "교대역": station_0,
    "사당역": station_1,
    "종로3가역": station_2,
    "서울역": station_3
}

• 동적 배열인 리스트에 노드들을 저장한다면 인덱스를 고유값으로 사용할 수 있다.
• 해시 테이블인 딕셔너리에 노드들을 저장한다면 중복되지 않는 고유 데이터 값을 키로 설정해야 한다.

4. 엣지 구현

인접 행렬

• 노드들의 edge를 나타내는 2차원 리스트
  
  
  

인접 리스트

• 그래프 노드가 연결된 노드들에 대한 레퍼런스를 저장하는 리스트
  
  
  

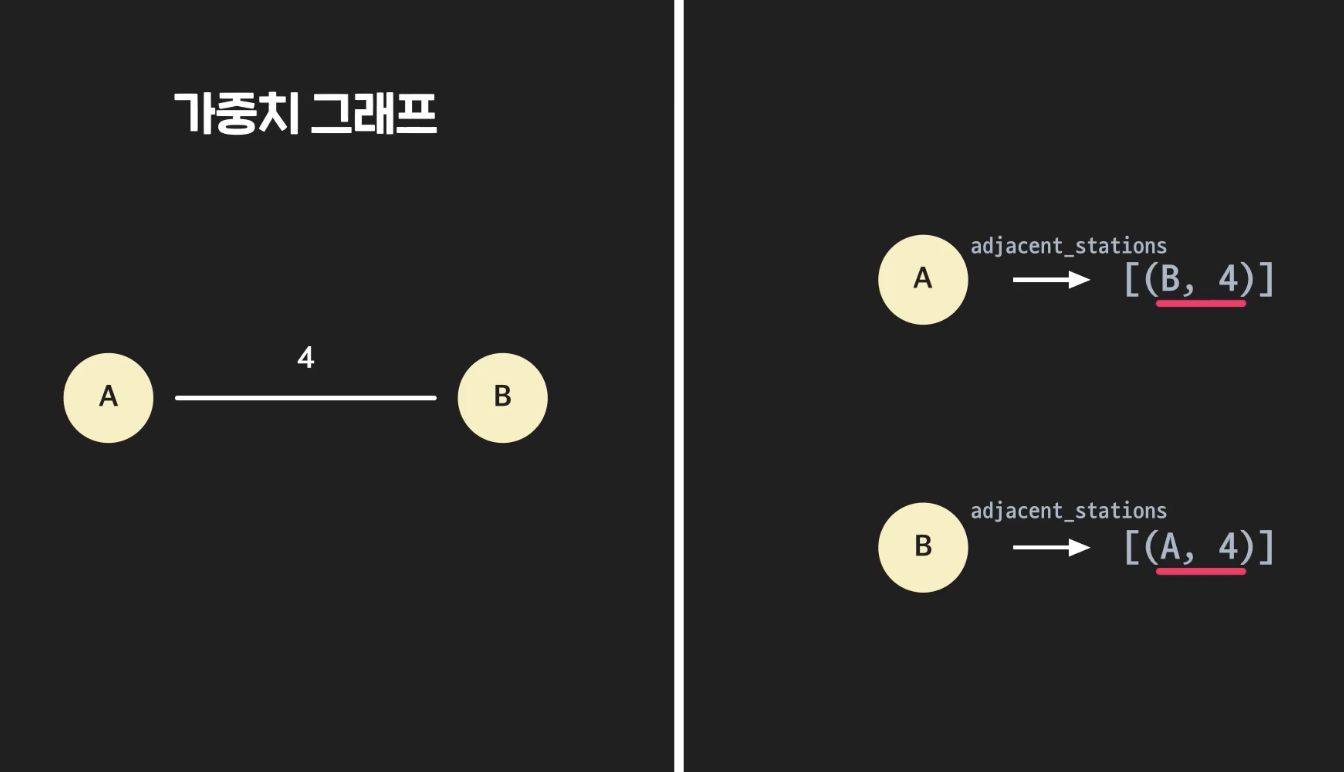
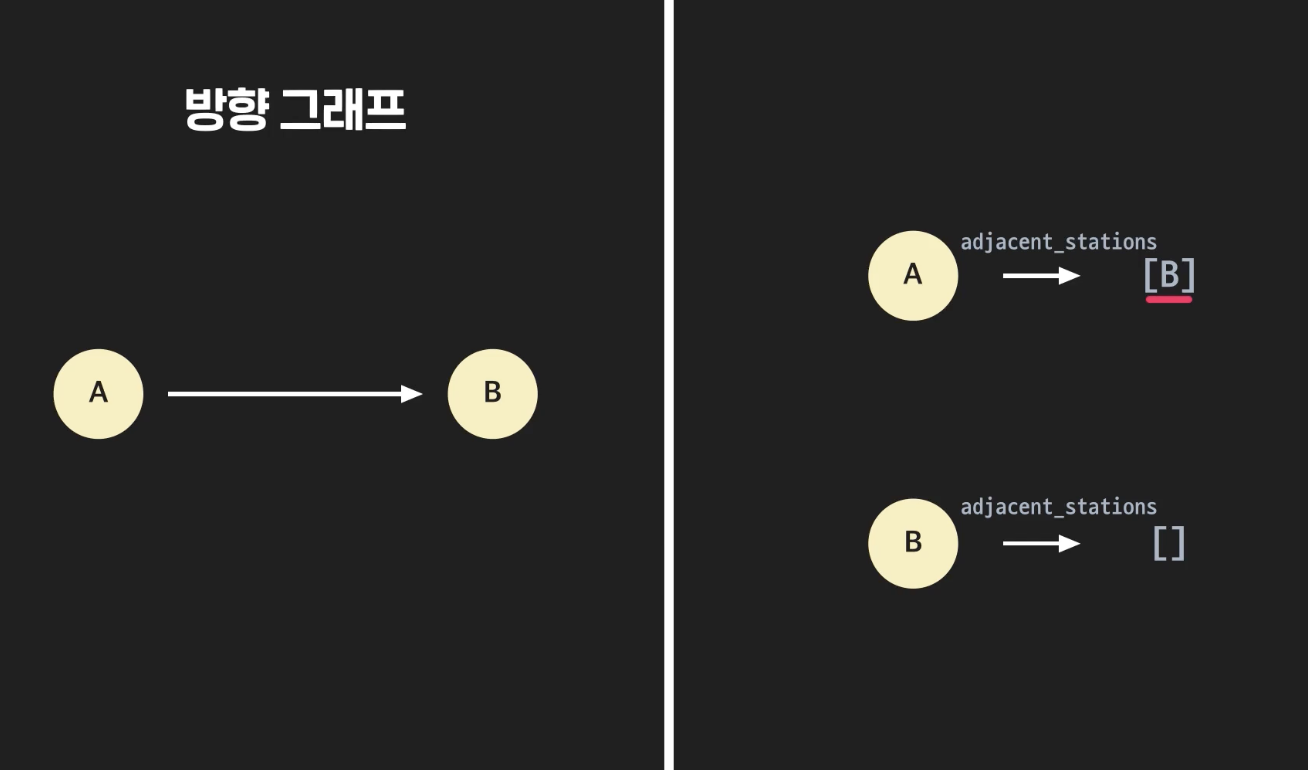
5. 인접 행렬 vs 인접 리스트

복잡도 표현 기호

• V 모든 노드들의 집합
• E 모든 엣지들의 집합
• 점근 표기법을 사용할 때 집합이 아닌 갯수를 의미한다.
• V와 E의 관계
  • 무방향 그래프: E = (V^2)/2 (worst-case)
  • 방향 그래프: E = V^2 (worst-case)

그래프 공간 복잡도

• 노드를 저장하는 공간: O(V)
• 엣지를 저장하는 공간: O(E)
• 인접 행렬이 차지하는 공간: O(V^2)
• 인접 리스트가 차지하는 공간: O(V)

두 노드가 연결됐는지 확인하는 데 걸리는 시간

• 인접 행렬
  • Worst-case time complexity: O(1)
  • Best-case time complexity: O(1)
  • Average time complexity: O(1)
• 인접 리스트: O(V)
  • Worst-case time complexity: O(V)
  • Best-case time complextiy: O(1)
  • Average time complexity: O(deg(V))

한 노드에 연결된 모든 노드들을 알아내는데(finding neighbors) 걸리는 시간

• 인접 행렬
  • Worst-case time complexity: O(V)
  • Best-case time complexity: O(V)
  • Average time complexity: O(V)
• 인접 리스트: O(V)
  • Worst-case time complexity: O(V)
  • Best-case time complextiy: O(1)
  • Average time complexity: O(deg(V))

Feedback

1. 그래프 연산의 시간, 공간 복잡도를 분석해보자.
2. 언어별로 그래프를 구현해보자.
3. 그래프 추상 자료형을 찾아보자.

참고 자료

• Graph (abstract data type) - Wikipedia
• Basic Graph Theory
• Multiple edges - Wikipedia
• 그래프 - 알고리즘 · 자료구조 강의 | 코드잇