1. 스택(Stack)
스택과 스택 메서드
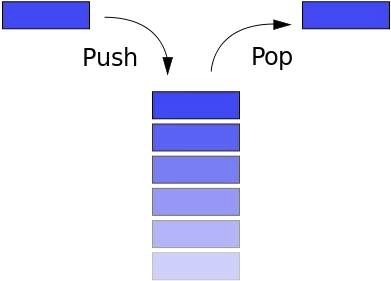
스택은 요소들의 컬렉션(collection) 역할을 하는 추상 자료형(abstract data type)입니다. 스택은 두 가지 main operations을 수행합니다:
Push맨 위에 새 요소를 삽입Pop맨 윗 요소를 삭제하고 리턴
추가적으로 다음 operations를 사용할 수 있습니다:
peek맨 윗 요소를 리턴size스택의 요소 갯수를 리턴
이러한 구조를 스택이라고 부르는 것은 접시 더미(stack of plates)처럼 물건이 다른 물건 위에 쌓이는(stacked) 물리적 집합에 비유한 것입니다.
스택은 LIFO(Last In First Out) 구조입니다. 스택 맨 위의 요소는 바로 추출할 수 있지만, 스택의 더 깊은 곳에 있는 데이터에 접근하려면 위에 쌓인 요소들을 먼저 제거해야 합니다.
스택은 선형 자료 구조(linear data structure) 또는 더 추상적이게 순차적 컬렉션(sequential collection)으로 분류됩니다. 스택에서 push, pop 연산은 스택의 맨 위에서만 발생합니다. 스택은 싱글리 링크드 리스트(singly linked list)와 최상위 요소에 대한 포인터로 구현할 수 있습니다. 그리고 제한된 용량(bounded capacity)를 갖도록 구현할 수 있습니다. 스택이 가득 차서 다른 요소를 추가할 공간이 없을 경우 스택 오버플로우(stack overflow) 상태가 됩니다.
스택은 Depth-first search(DFS) 등을 구현할 때 필요합니다.
자바스크립트로 스택 구현하기
자바스크립트의 배열(Array)는 스택의 속성들을 이미 갖고 있습니다. 그렇지만 function Stack()을 이용하여 스택을 처음부터(from scratch) 구성해 봅시다:
function Stack() {
this.count = 0;
this.storage = {};
this.push = function (value) {
this.storage[this.count] = value;
this.count++;
}
this.pop = function () {
if (this.count === 0) {
return undefined;
}
this.count--;
const result = this.storage[this.count];
delete this.storage[this.count];
return result;
}
this.peek = function () {
return this.storage[this.count - 1];
}
this.size = function () {
return this.count;
}
}
2. 큐(Queue)

큐와 큐 메서드
큐는 시퀀스(sequence)에 유지되는 요소들의 컬렉션으로, 시퀀스의 한쪽 끝에 요소를 삽입하고 다른 쪽 끝에서 요소를 삭제하여 수정할 수 있는 추상 자료형입니다. 일반적으로 요소가 삽입되는 시퀀스의 끝을 큐의 back, tail 또는 rear이라고 하고, 요소가 삭제되는 시퀀스의 끝을 큐의 front 또는 head라고 합니다. 큐는 두 가지 main operations을 수행합니다:
enqueueEnter queue, back에 요소를 삽입dequeueLeave queue, front 요소를 삭제하고 리턴
추가적으로 다음 operations를 사용할 수 있습니다:
peekfront 요소를 리턴isEmpty큐가 비어있는 지에 대한 불린 값 리턴size큐의 요소 갯수를 리턴
큐는 사람들이 상품이나 서비스를 기다리기 위해 줄을 설 때 사용하는 단어입니다.
큐은 FIFO(First In First Out) 구조입니다. 큐의 front 요소는 바로 추출할 수 있지만, front의 뒷 쪽에 있는 데이터에 접근하려면 앞에 쌓인 요소들을 먼저 제거해야 합니다.
큐는 선형 자료 구조 또는 더 추상적이게 순차적 컬렉션으로 분류됩니다.큐는 동적 배열(dynamic array) 또는 더블리 링크드 리스트(doubly linked list)로 구현할 수 있습니다. 큐가 비어있을 때 요소에 접근할 때 Queue underflow가 발생하고 큐가 가득 찼을 때 Queue overflow가 발생합니다.
큐는 버퍼(buffer)의 기능을 수행할 수 있고, Breadth-first search(BFS) 등을 구현할 때 필요합니다.
자바스크립트로 큐 구현하기
자바스크립트의 배열는 큐의 몇 가지 속성들을 이미 갖고 있습니다. 그러므로 큐를 구현할 때 배열을 활용할 수 있습니다:
function Queue() {
const collection = [];
this.print = function () {
console.log(collection);
}
this.enqueue = function (element) {
collection.push(element);
}
this.dequeue = function () {
return collection.shift();
}
this.peek = function () {
return collection[0];
}
this.isEmpty = function () {
return collection.length === 0;
}
this.size = function () {
return collection.length;
}
}
우선순위 큐(Priority queue)
우선순위 큐는 우선순위가 높은 요소부터 순서대로 나오는 큐입니다. 우선순위 큐는 힙을 사용하여 구현되는 경우가 많습니다:
class Heap {
constructor() {
this.heap = [];
}
// 두 노드의 위치를 바꿔주는 메소드
swap(index1, index2) {
[this.heap[index1], this.heap[index2]] = [this.heap[index2], this.heap[index1]];
}
// 삽입된 노드를 힙 속성을 만족시키는 위치로 이동시키는 메소드
reverseHeapify(index) {
const parentIndex = Math.floor((index - 1) / 2);
if (parentIndex >= 0 && this.heap[index] > this.heap[parentIndex]) {
this.swap(index, parentIndex);
this.reverseHeapify(parentIndex);
}
}
// 배열을 힙으로 만드는 메소드
heapify(index) {
const leftChildIndex = 2 * index + 1;
const rightChildIndex = 2 * index + 2;
let largest = index;
if (leftChildIndex < this.heap.length && this.heap[largest] < this.heap[leftChildIndex]) {
largest = leftChildIndex;
}
if (rightChildIndex < this.heap.length && this.heap[largest] < this.heap[rightChildIndex]) {
largest = rightChildIndex;
}
if (largest !== index) {
this.swap(index, largest);
this.heapify(largest);
}
}
// 삽입 메소드
insert(data) {
this.heap.push(data);
this.reverseHeapify(this.heap.length - 1);
}
// 최우선순위 데이터 추출 메소드
extractMax() {
if (this.heap.length <= 0) {
return null;
}
if (this.heap.length === 1) {
return this.heap.pop();
}
const max = this.heap[0];
this.heap[0] = this.heap.pop();
this.heapify(0);
return max;
}
// 힙 출력 메소드
print() {
console.log(this.heap);
}
}
// 힙으로 구현한 우선순위 큐
class PriorityQueue {
constructor() {
this.heap = new Heap();
}
// 삽입 메소드
enqueue(data) {
this.heap.insert(data);
}
// 최우선순위 데이터 추출 메소드
dequeue() {
return this.heap.extractMax();
}
// PriorityQueue 출력 메소드
print() {
this.heap.print();
}
}
3. 링크드 리스트(Linked List)
링크드 리스트와 링크드 리스트 메서드
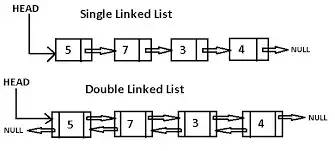
링크드 리스트는 순서가 메모리 내 물리적 배치 순서를 따르지 않는 데이터 요소의 선형 컬렉션입니다. 각 요소가 다음 요소를 가리키는 참조(reference)를 저장하는 방식으로 순서를 정의합니다. 링크드 리스트를 구성하는 요소를 노드라고 합니다. 각 요소가 다음 요소의 참조만 가지고 있는 것을 싱글리 링크드 리스트(singly linked list)라고 하고, 이전 요소의 참조도 가지고 있는 것을 더블리 링크드 리스트(doubly linked list)라고 합니다. 링크드 리스트는 네 가지 main operations을 수행합니다:
prepend새로운 노드를 맨 앞(head)로 삽입append새로운 노드를 맨 뒤(tail)로 삽입insert_after전달받은 노드의 다음 위치에 새로운 노드를 삽입pop_lefthead 노드를 삭제하고 리턴delete_after전달 받은 노드의 다음 노드를 삭제하고 리턴
추가적으로 다음 operations를 사용할 수 있습니다:
headhead 요소를 리턴elementAt아규먼트로 받은 인덱스의 노드를 리턴indexOf아규먼트로 받은 노드의 인덱스를 리턴size링크드 리스트의 노드 갯수를 리턴
링크드 리스트를 사용하면 반복문에서 시퀀스의 어느 위치에서나 효율적으로 요소를 삽입 또는 삭제할 수 있습니다. 링크드 리스트의 단점은 선형적 구조이기 때문에 랜덤 액세스보다 접근 속도가 느리고, 파이프라인(pipeline)화 하기 어렵다는 점입니다. 배열은 링크드 리스트에 비해 캐시 로컬리티(cache locality)가 우수합니다.
링크드 리스트는 단순하고 일반적인 자료 구조 중 하나입니다. 링크드 리스트는 리스트, 스택, 큐, 연관 배열(associative arrays), 또는 S-expressions 등을 구현하는 데에도 사용될 수 있습니다.
자바스크립트로 링크드 리스트 구현하기
class Node {
constructor(data) {
this.data = data;
this.next = null;
}
}
class LinkedList {
constructor() {
this.head = null;
this.tail = null;
this.size = 0;
}
pop_left() {
const data = this.head.data;
if (this.head === this.tail) {
this.head = null;
this.tail = null;
} else {
this.head = this.head.next;
}
if (this.size > 0) {
this.size--;
}
return data;
}
head() {
return this.head.data;
}
delete_after(previous_node) {
const data = previous_node.next.data;
if (previous_node.next === this.tail) {
previous_node.next = null;
this.tail = previous_node;
} else {
previous_node.next = previous_node.next.next;
}
if (this.size > 0) {
this.size--;
}
return data;
}
prepend(data) {
const new_node = new Node(data);
if (this.head === null) {
this.tail = new_node;
} else {
new_node.next = this.head;
}
this.size++;
this.head = new_node;
}
insert_after(previous_node, data) {
const new_node = new Node(data);
if (previous_node === this.tail) {
this.tail.next = new_node;
this.tail = new_node;
} else {
new_node.next = previous_node.next;
previous_node.next = new_node;
}
this.size++;
}
elementAt(index) {
let iterator = this.head;
for (let i = 0; i < index; i++) {
iterator = iterator.next;
}
return iterator;
}
indexOf(data) {
let iterator = this.head;
while (iterator !== null) {
if (iterator.data === data) {
return iterator;
}
iterator = iterator.next;
}
return null;
}
append(data) {
const new_node = new Node(data);
if (this.head === null) {
this.head = new_node;
this.tail = new_node;
} else {
this.tail.next = new_node;
this.tail = new_node;
}
this.size++;
}
toString() {
let res_str = "|";
let iterator = this.head;
while (iterator !== null) {
res_str += ` ${iterator.data} |`;
iterator = iterator.next;
}
return res_str;
}
}
4. 세트(Set)

세트와 세트 메서드
세트는 특정한 순서 없이 고유한 값을 저장할 수 있는 추상 자료형입니다. 세트는 5가지 main operations을 수행합니다:
add원소 삽입remove원소 삭제union두 세트 사이의 겹치는 원소를 담은 세트를 리턴difference두 세트 사이의 겹치지 않는 원소를 담은 세트를 리턴subset특정 세트가 다른 세트의 subset인지에 대한 boolean 값을 리턴
추가적으로 다음 operations를 사용할 수 있습니다:
values세트의 모든 원소 리턴size세트의 원소 갯수를 리턴
세트는 유한 집합의 수학적 개념을 컴퓨터로 구현한 것입니다. 대부분의 다른 컬렉션 유형과 달리 세트에서 특정 요소를 검색하기 위해 사용되기 보다는 데이터가 세트의 원소인지 테스트하기 위해 사용됩니다.
세트에는 정적 세트(Static set)와 동적 세트(Dynamic set)가 있습니다.
자바스크립트로 세트 구현하기
ES6에서 배열과 유사하지만 반복되는 요소를 허용하지 않으며 인덱싱되지 않는 set라는 개념이 도입되었습니다. ES6의 set와 구분하기 위해 다음 예제에서는 MySet으로 선언합니다:
function MySet() {
const collection = [];
this.has = (element) => (collection.indexOf(element) !== -1);
this.values = () => collection;
this.size = () => collection.length;
this.add = (element) => {
if (!this.has(element)) {
collection.push(element);
return true;
}
return false;
};
this.remove = (element) => {
if (this.has(element)) {
const index = collection.indexOf(element);
collection.splice(index, 1);
return true;
}
return false;
};
this.union = (otherSet) => {
if (!(otherSet instanceof MySet)) {
throw new Error("Invalid argument type");
}
const unionSet = new MySet();
const firstSet = this.values();
const secondSet = otherSet.values();
firstSet.forEach(function (e) {
unionSet.add(e);
});
secondSet.forEach(function (e) {
unionSet.add(e);
});
return unionSet;
};
this.intersection = (otherSet) => {
if (!(otherSet instanceof MySet)) {
throw new Error("Invalid argument type");
}
const intersectionSet = new MySet();
const firstSet = this.values();
firstSet.forEach(function (e) {
if (otherSet.has(e)) {
intersectionSet.add(e);
}
});
return intersectionSet;
};
this.difference = (otherSet) => {
if (!(otherSet instanceof MySet)) {
throw new Error("Invalid argument type");
}
const differenceSet = new MySet();
const firstSet = this.values();
firstSet.forEach(function (e) {
if (!otherSet.has(e)) {
differenceSet.add(e);
}
});
return differenceSet;
};
this.subset = (otherSet) => {
if (!(otherSet instanceof MySet)) {
throw new Error("Invalid argument type");
}
const firstSet = this.values();
return firstSet.every(function (value) {
return otherSet.has(value);
});
};
}
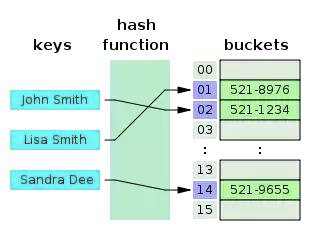
5. 해시 테이블(Hash Table)
해시 테이블과 해시 테이블 메서드
해시 테이블 참조
해시 테이블은 세 가지 main operations을 수행합니다:
addkey-value 쌍 삽입removekey-value 쌍 삭제lookup전달받은 key에 해당하는 value 리턴
자바스크립트로 해시 테이블 구현하기
자바스크립트의 객체(Object)는 내부적으로 해시 테이블 구조를 사용하지만, 별도로 충돌을 처리하는 방법이 필요합니다. 때문에 일반적으로 객체 대신 Map 클래스를 사용하거나, 해시 함수를 직접 구현하여 해시 충돌을 최소화하는 방법 등을 사용합니다.
다음 예시는 링크드 리스트로 구현한 해시 테이블 예시입니다:
class Node {
constructor(key, value) {
this.key = key;
this.value = value;
this.next = null;
this.prev = null;
}
}
class LinkedList {
constructor() {
this.head = null;
this.tail = null;
}
find_node_with_key(key) {
let iterator = this.head;
while (iterator !== null) {
if (iterator.key === key) {
return iterator;
}
iterator = iterator.next;
}
return null;
}
append(key, value) {
const new_node = new Node(key, value);
if (this.head === null) {
this.head = new_node;
this.tail = new_node;
} else {
this.tail.next = new_node;
new_node.prev = this.tail;
this.tail = new_node;
}
}
delete(node_to_delete) {
if (node_to_delete === this.head && node_to_delete === this.tail) {
this.tail = null;
this.head = null;
} else if (node_to_delete === this.head) {
this.head = this.head.next;
this.head.prev = null;
} else if (node_to_delete === this.tail) {
this.tail = this.tail.prev;
this.tail.next = null;
} else {
node_to_delete.prev.next = node_to_delete.next;
node_to_delete.next.prev = node_to_delete.prev;
}
return node_to_delete.value;
}
toString() {
let res_str = "";
let iterator = this.head;
while (iterator !== null) {
res_str += `${iterator.key}: ${iterator.value}\n`;
iterator = iterator.next;
}
return res_str;
}
}
class HashTable {
constructor(capacity) {
this._capacity = capacity;
this._table = new Array(capacity);
for (let i = 0; i < capacity; i++) {
this._table[i] = new LinkedList();
}
}
_hash_function(key) {
return Math.abs(hashCode(key)) % this._capacity;
}
_get_linked_list_for_key(key) {
const hashed_index = this._hash_function(key);
return this._table[hashed_index];
}
_look_up_node(key) {
const linked_list = this._get_linked_list_for_key(key);
return linked_list.find_node_with_key(key);
}
look_up_value(key) {
return this._look_up_node(key).value;
}
insert(key, value) {
const existing_node = this._look_up_node(key);
if (existing_node !== null) {
existing_node.value = value;
} else {
const linked_list = this._get_linked_list_for_key(key);
linked_list.append(key, value);
}
}
delete_by_key(key) {
const node_to_delete = this._look_up_node(key);
if (node_to_delete !== null) {
const linked_list = this._get_linked_list_for_key(key);
linked_list.delete(node_to_delete);
}
}
toString() {
let res_str = "";
for (const linked_list of this._table) {
res_str += linked_list.toString();
}
return res_str.slice(0, -1);
}
}
function hashCode(key) {
if (typeof key === 'string') {
let hash = 0;
for (let i = 0; i < key.length; i++) {
hash = (hash << 5) - hash + key.charCodeAt(i);
hash |= 0; // Convert to 32bit integer
}
return hash;
} else if (typeof key === 'number') {
return key;
} else if (typeof key === 'object') {
return hashCode(JSON.stringify(key));
} else {
throw new Error('Unsupported key type');
}
}
6. 트리(Tree)
트리와 트리 메서드
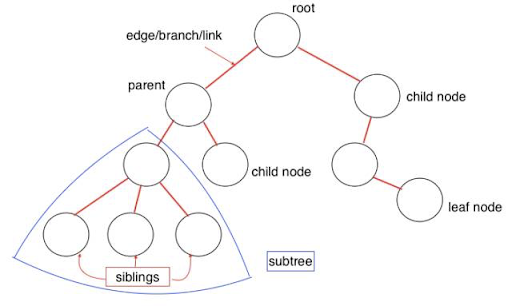
트리는 연결된 노드 집합이 있는 계층적 트리 구조를 나타내는 추상 자료형입니다.
- 트리 개념들
root트리의 뿌리 노드; 부모가 없습니다.parent node상위 계층의 직접 노드; 하나만 있습니다.child node하위 계층의 직접 노드; 여러 개를 가질 수 있습니다.siblings부모 노드를 공유합니다.leaf자식이 없는 노드Edge두 노드 사이를 연결하는 변Path시작 노드에서 대상 노드까지의 edgeHeight of Node특정 노드에서 리프 노드까지의 가장 긴 경로의 edge 수Height of Tree루트 노드에서 리프 노드까지의 최장 경로의 edge 수Depth of Node루트 노드에서 특정 노드까지의 edge 수Degree of Node자식 노드의 수
트리의 각 노드는 트리 유형에 따라 여러 자식에 연결될 수 있지만, 부모가 없는 루트 노드를 제외하고 정확히 하나의 부모에 연결되어야 합니다. 이러한 제약 조건은 주기나 "루프"가 없으며 각 자식이 자신의 하위 트리의 루트 노드처럼 취급될 수 있다는 것을 의미하므로 재귀는 트리 탐색에 유용한 기법입니다. 선형 데이터 구조와 달리, 많은 트리는 인접 노드 간의 관계를 하나의 직선으로 표현할 수 없습니다.
이진 탐색 트리(Binary Search Tree)

이진 트리(Binary Tree)는 각 부모에 대한 자식 수를 최대 2개로 제한합니다. 부모 자식간의 대소 관계를 정해놓고 규칙에 맞게 정렬된 이진 트리를 이진 탐색 트리라고 합니다. 이진 탐색 트리는 세 가지 main operations을 수행합니다:
add새로운 노드를 삽입find주어진 값에 해당하는 노드를 탐색remove주어진 값을 갖는 노드를 삭제
추가적으로 다음 operations를 사용할 수 있습니다:
findMin최솟값 노드를 리턴findMax최댓값 노드를 리턴isPresent특정 값을 갖는 노드가 있는지에 대한 Boolean 값 리턴
자바스크립트로 이진 탐색 트리 구현하기
class Node {
constructor(data, left = null, right = null) {
this.data = data;
this.left = left;
this.right = right;
}
}
class BST {
constructor() {
this.root = null;
}
add(data) {
const node = this.root;
if (node === null) {
this.root = new Node(data);
return;
} else {
const searchTree = function (node) {
if (data < node.data) {
if (node.left === null) {
node.left = new Node(data);
return;
} else if (node.left !== null) {
return searchTree(node.left);
}
} else if (data > node.data) {
if (node.right === null) {
node.right = new Node(data);
return;
} else if (node.right !== null) {
return searchTree(node.right);
}
} else {
return null;
}
};
return searchTree(node);
}
}
findMin() {
let current = this.root;
while (current.left !== null) {
current = current.left;
}
return current.data;
}
findMax() {
let current = this.root;
while (current.right !== null) {
current = current.right;
}
return current.data;
}
find(data) {
let current = this.root;
while (current.data !== data) {
if (data < current.data) {
current = current.left
} else {
current = current.right;
}
if (current === null) {
return null;
}
}
return current;
}
isPresent(data) {
let current = this.root;
while (current) {
if (data === current.data) {
return true;
}
if (data < current.data) {
current = current.left;
} else {
current = current.right;
}
}
return false;
}
remove(data) {
const removeNode = function (node, data) {
if (node == null) {
return null;
}
if (data == node.data) {
// no child node
if (node.left == null && node.right == null) {
return null;
}
// no left node
if (node.left == null) {
return node.right;
}
// no right node
if (node.right == null) {
return node.left;
}
// has 2 child nodes
let tempNode = node.right;
while (tempNode.left !== null) {
tempNode = tempNode.left;
}
node.data = tempNode.data;
node.right = removeNode(node.right, tempNode.data);
return node;
} else if (data < node.data) {
node.left = removeNode(node.left, data);
return node;
} else {
node.right = removeNode(node.right, data);
return node;
}
}
this.root = removeNode(this.root, data);
}
}
7. 트라이(Trie)
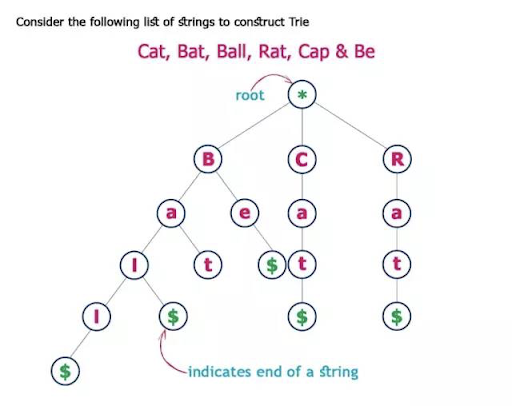
트라이와 트라이 메서드
트라이는 세트 내에서 특정 키를 찾는 데 사용되는 트리 데이터 구조인 k-ary search tree의 한 유형으로 디지털 트리(digital tree) 또는 접두사 트리(prefix tree)라고도 부릅니다. 대부분 문자열 형태의 키를 다루는데, 각 노드 간 연결은 전체 키가 아니라 개별 문자를 나타냅니다. 따라서 원하는 키에 접근하려면, 트라이를 DFS를 시도하면서 노드 간 연결을 따라가야 합니다. 트라이의 각 노드에는 알파벳이 있으며, 그 가지를 따라가면 완전한 단어를 형성할 수 있습니다. 또한 문자열의 끝인지 여부를 표시하는 boolean indicator로 구성됩니다. 트라이는 세 가지 main operations을 수행합니다:
add단어를 트라이에 삽입isWord특정 단어를 트라이가 포함하고 있는지에 대한 boolean 값을 리턴print트라이의 모든 단어들을 리턴
트라이는 이진 탐색 트리와 달리, 노드가 관련된 키를 저장하지 않습니다. 대신, 트라이 내 노드의 위치가 연관된 키를 정의합니다. 이로 인해 각 키의 값이 데이터 구조 전체에 분산되며, 모든 노드가 값과 연관되어 있지 않을 수 있습니다.
부모 노드의 모든 자식 노드는 해당 부모 노드와 관련된 문자열의 공통 접두어를 가지며, 루트는 빈 문자열과 연관됩니다. 이러한 접두어로 데이터를 저장하는 작업은 radix 트리를 사용하여 메모리를 최적화하는 방식으로 수행할 수 있습니다.
트라이는 단어장을 저장하거나 자동완성 기능 등에서 빠른 검색을 가능하게 해주는 추상 자료형입니다.
자바스크립트로 트라이 구현하기
class Node {
constructor() {
this.keys = new Map();
this.end = false;
}
setEnd() {
this.end = true;
}
isEnd() {
return this.end;
}
}
class Trie {
constructor() {
this.root = new Node();
}
add(input, node = this.root) {
if (input.length === 0) {
node.setEnd();
return;
} else if (!node.keys.has(input[0])) {
node.keys.set(input[0], new Node());
return this.add(input.substr(1), node.keys.get(input[0]));
} else {
return this.add(input.substr(1), node.keys.get(input[0]));
}
}
isWord(word) {
let node = this.root;
while (word.length > 1) {
if (!node.keys.has(word[0])) {
return false;
} else {
node = node.keys.get(word[0]);
word = word.substr(1);
}
}
return node.keys.has(word) && node.keys.get(word).isEnd() ? true : false;
}
print() {
let words = new Array();
let search = function(node = this.root, string) {
if (node.keys.size !== 0) {
for (let letter of node.keys.keys()) {
search(node.keys.get(letter), string.concat(letter));
}
if (node.isEnd()) {
words.push(string);
}
} else {
string.length > 0 ? words.push(string) : undefined;
return;
}
};
search(this.root, new String());
return words.length > 0 ? words : null;
}
}
Feedback
- 다음으로 구현한 추상 자료형들의 기본 연산 performance를 분석하자.
- 그래프, BFS, DFS도 자바스크립트 코드로 옮기자. (내용이 길어서 따로 포스팅하자)
Reference
