데브코스 35일차 - 데이터 모델링(2)

키워드

평가/분석 방법

Naive Bayes

• 문 같이 생긴 기호가 product
• sklearn.naive_bayes의 CaussianNB를 import 해 사용

Evaluation

• 모델을 어떻게 평가할지, 기준을 정해야함

• 회귀 평가 방법

  • MSE (Mean Squared Error)

    • 오차 제곱의 평균
    • 오차값이 큰 데이터점(outlier)에 대해 민감하게 반응 ! 유의

  • MAE (Mean Absolute Error)

    • 오차의 절대값의 평균
    • 오차값이 큰 데이터점에 대해 MSE 대비 덜 민감하게 반응

  • R-squared (결정계수)

    

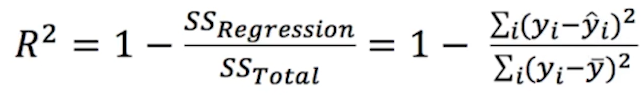
    • 독립변수 x가 종속변수 y(분산)를 얼마나 잘 설명하는지를 나타냄, 이 값이 1에 가까울 수록 X와 Y가 선형관계를 갖는다! 라고 할 수 있음
    • 전체 관측값 y의 평균(y 바)으로부터 각 y값이 멀리 떨어질수록, 예측한 y값과 실제 y값이 가까울수록 1에 가까워짐
      • 즉 관측값과 평균 사이 오차 제곱(종속 변수의 분산)이 커질수록, 오차 제곱(예측 오차, 잔차)가 작을 수록 좋은 값을 가짐
      • 만약 모델의 예측값이 샘플 평균보다 낮으면 결정계수는 마이너스 값을 가짐

• 분류 평가 방법

  • 분류 성능 평가 지표
    • (분류값이 정답인지 아닌지: True/False)(분류한 것: Positive/Negative)
    • ex) FN: 네거티브(N)로 분류했는데 틀림(F) → 사실은 True
  • precision
    • 실제로 positive인 샘플 중 몇 개를 positive로 분류했는지
    • TP / TP+FP
  • recall
    • positive로 분류한 샘플 중 몇 개가 실제 positive인지
    • TP / TP+FN
  • precision, recall은 positive threshold로 조절이 가능
  • FP가 늘어나는 것이 문제인 경우엔 precision을 높이는 것이 중요하지만,
    FP가 늘어나도 어떻게든 positive를 잡아내야되는 경우(전염병, 암 진단) recall을 높이는 것이 중요
    - precision이 중요한지, recall이 중요한지 잘 판단해야함
  • F1-score (precision과 recall의 조화평균)
    • 2precisionrecall / precision+recall
    • 조화평균은 역수의 산술평균의 역수를 의미한다.
    • precision과 recall을 둘 다 고려한 metric이다.
    • 둘 중 작은 값에 영향을 많이 받음 → 즉 둘 다 균형있게 좋은 값을 내야 좋은 f1 값을 냄

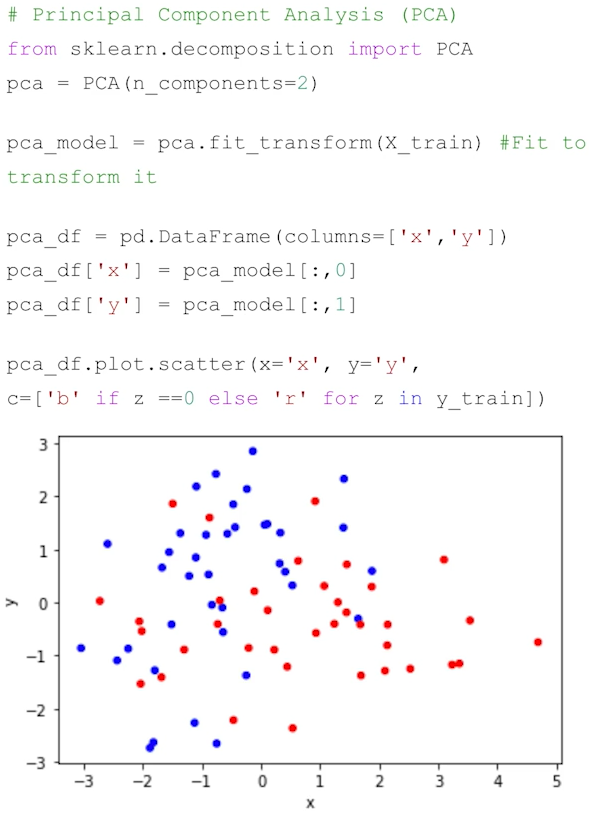
PCA

• Principal component analysis (주성분 분석)
  • 주성분: 데이터들의 분산이 가장 큰 방향벡터
  • 고차원(feature가 많은) x에 대해서 데이터의 분포를 가장 잘 설명하는 새로운 축을 찾아내는 기술 (차원축소)
  • 새로운 축(PC)은 각 점들이 퍼져있는 정도인 분산이 최대로 보존될 수 있도록 해야함
  • 분산이 커져야 데이터들 사이의 차이점이 명확해지고 그것이 모델을 더 좋은 방향으로 만들 수 있을 것이기 때문에

• 각 x의 평균값을 새로운 축으로 설정 → 새로운 축들의 교차점이 원점이 되도록
• 수선의 발과 원점 사이의 거리의 제곱들의 합(SS)이 최대가 되는 축을 PC1으로, 또 그에 직교하는 축을 PC2로 설정. N개의 PC 축 설정

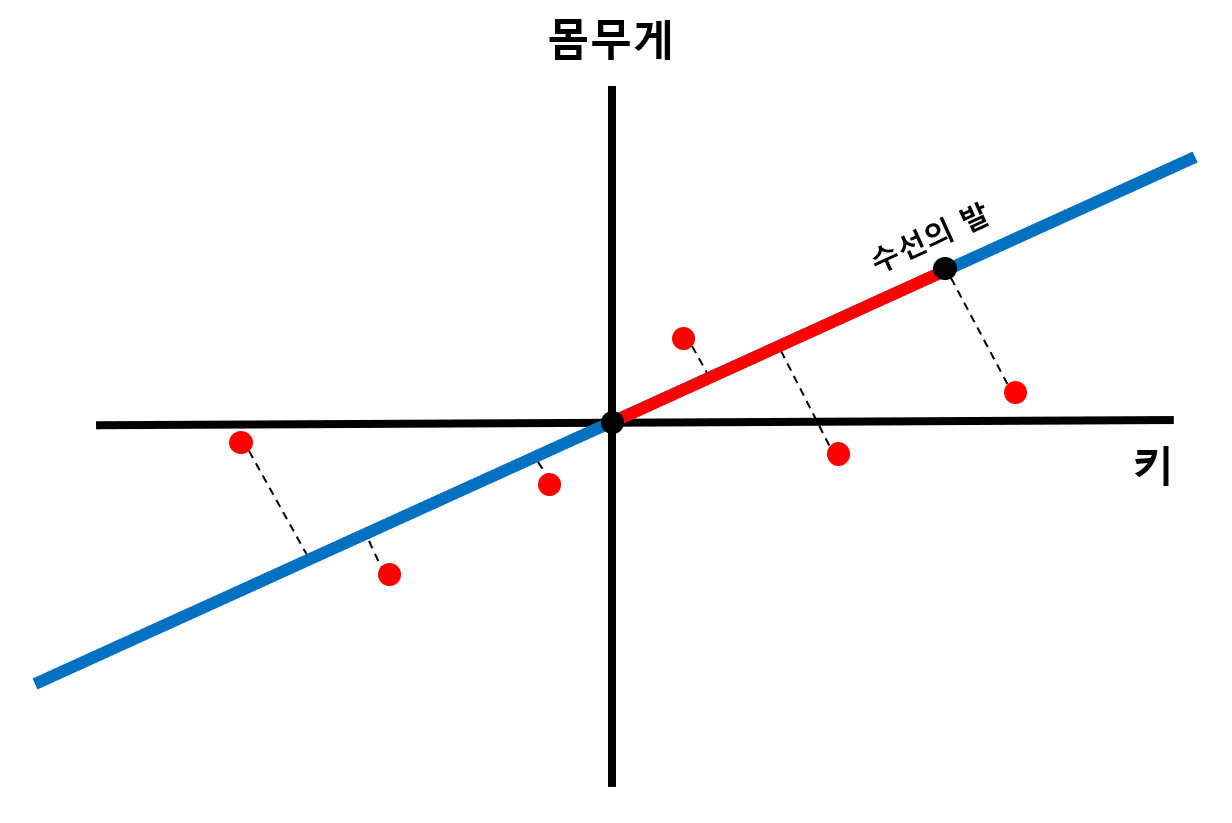
• 모델의 feature 개수를 줄여 효과적인 학습을 목표로 함
• 하지만 이 좌표의 의미를 해석하기 쉽진 않음

Feature Analysis

• 어떤 feature가 y를 설명하는 데 있어 중요한 feature인지 아는 것 또한 매우 중요
• LogisticRegression(), LinearRegression(), SVC이 학습 된 상태에서 .coef와 .intercept를 조회
  • .coef_: feature들에 대해서 각각 곱해지는 값을 의미, 가중치
  • .intercept_: 절편을 의미

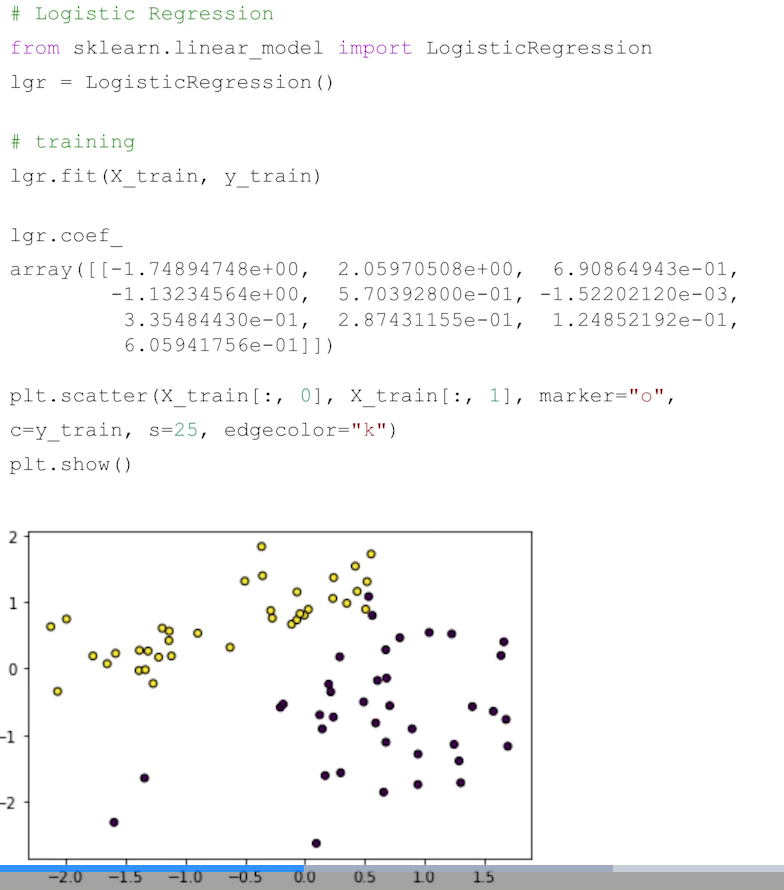
• 실제로 coef의 절대값이 큰 feature만 뽑아서 scatter로 그려보면 클래스별 구분이 되어있는 것을 볼 수 있음 → label을 잘 설명하는 feature!

• Random Forest 모델들에서는 자체적으로 feature_importances_를 제공

상관관계 분석

• feature들과 label 간의 상관관계 분석을 통해 feature의 중요도를 알아볼 수 있다.
• 상관관계: 다른 두 통계적 변인이 공변하는 함수관계 (not 인과관계!!)
• scipy.stats에서 import 해 사용 가능
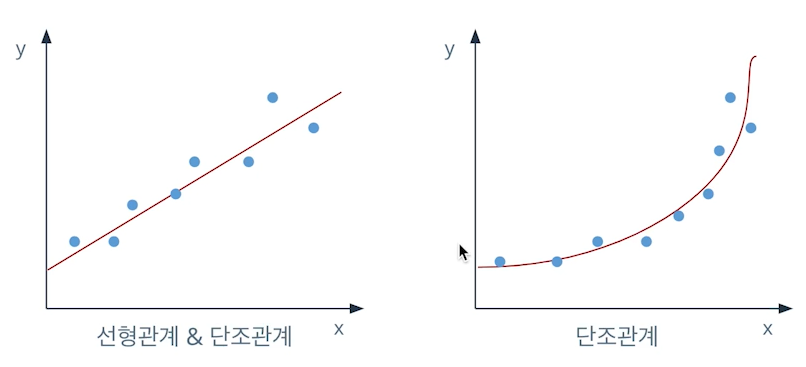
• 피어슨 상관계수 (pearsonr())
  • 두 변수간의 선형 상관관계의 정도를 나타냄
• 스피어만 상관계수 (spearmanr())
  • 두 변수간의 크기 순서상의 상관관계의 정도를 나타냄
  • 단조관계만 유지되면 잘 나옴

    • 단조관계: 두 변수가 함께 증가하지만 같은 비율로 증가하진 않는 관계

      

• 두 상관계수 모두 1/-1에 가까울 수록 양/음의 상관관계가 있다고 할 수 있다
• 같이 나오는 p-value(가설검정)의 경우 ‘H0: 두 변수는 상관관계가 없다’ 라고 하는 가설에 대한 p-value이다. 즉 p-value가 낮으면 두 변수가 상관관계가 있다고 볼 수 있음

궁금한 점

• R-squared에서 모델을 평가하는 데 왜 식에 라벨의 분산이 포함되는지 이해가 안된다.
• PCA에서 SS가 잘 이해가 되지 않는다. 원점과 수선의 발 사이 거리가 분산을 대표하는 건가?
• naive bayes는 통계 복습하고 와서 다시 봐야겠다.. 수식이 잘 이해가 안된다.