문제 링크
https://programmers.co.kr/learn/courses/30/lessons/62048#
문제 설명
임의의 사각형의 가로, 세로 길이가 인자로 주어진다. 이때 해당 사각형에 대각선을 그렸을 때 멀쩡한 사각형의 갯수를 반환하라
1차 시도
없다. 완전 처음엔 문제 보고 이게 뭐야. 수학 문제야 뭐야. 했다.
다시 풀려고 본 오늘은 꾸역꾸역 규칙을 찾아냈다. 근데 너무 복잡하고 모든 케이스를 고려해서 코드를 작성해야했다.
코테 문제인데 이건 아닐텐데... 라는 생각을 계속 하면서 작성한 코드는 66.7점이었고 틀린 이유를 더이상 찾아내지 못했다.
답을 찾아보지 않겠다고 다짐한게 어젠데 너무 뚝심없게 봐버렸다 (물론 지금의 내가 하는 생각이다)
2차 시도
import math
def solution(w,h):
return w*h - (w+h-math.gcd(w,h))이게 무슨 말도 안되는 코드인가 싶겠지만 그동안 본 테스트 케이스에 모두 들어 맞는다.
- 여기서 math 라이브러리의 gcd는 최대공약수를 반환한다. (최대 공약수로 1이 반환될 수 있다.)
예를 들어 설명을 해보면
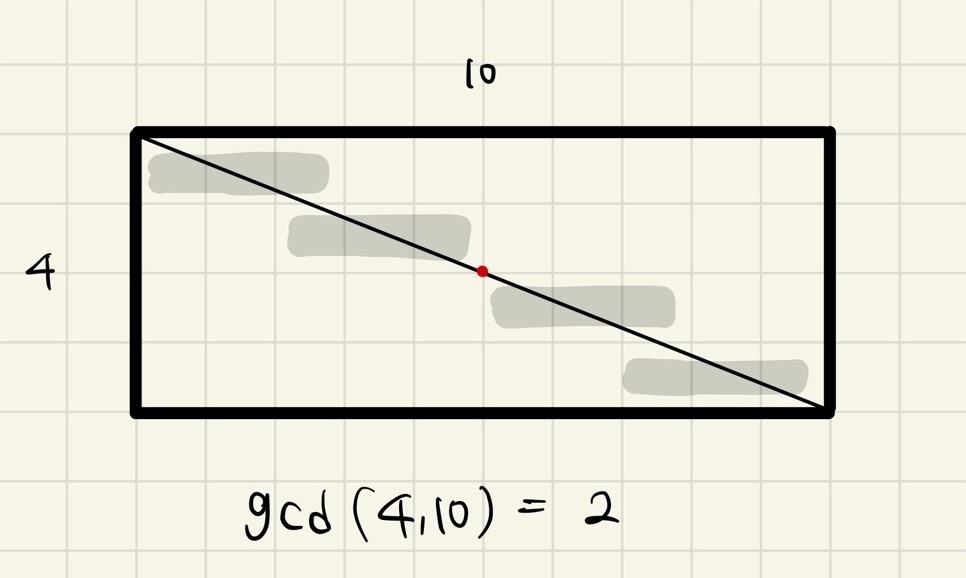
w = 10, h = 4의 사각형이 있다고 해보자.
대각선을 그으면 멀쩡하지 않은 사각형은 사진에서와 같이 회색으로 칠해진 12개의 사각형이다.
해당 대각선은 하나의 격자점에서 만나는데 이를 기준으로 멀쩡하지 않은 사각형을 묶어보면
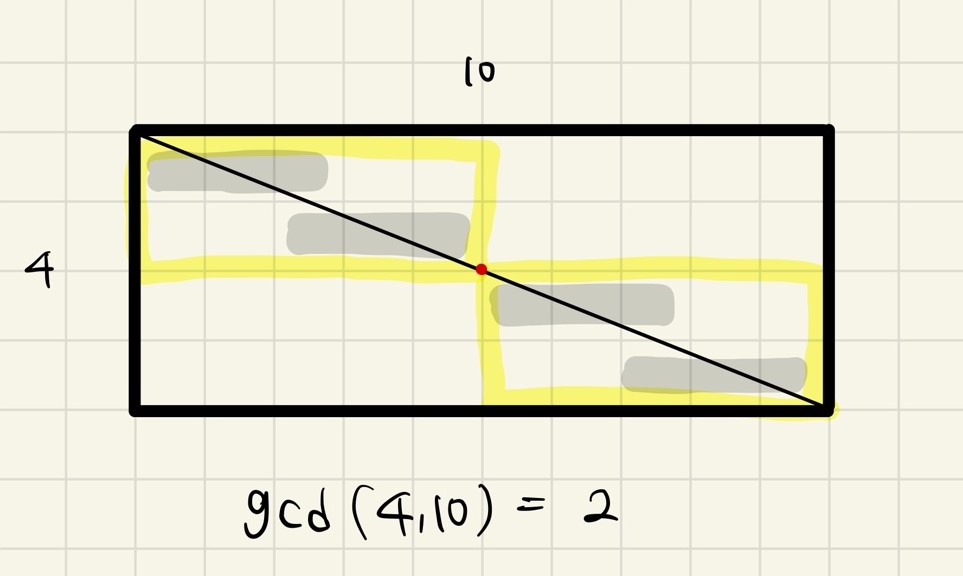
이렇게 나타난다.
어 묶음 사각형의 갯수가 가로, 세로 길이의 최대공약수와 같다.
그리고 회색칠의 위치를 조금만 옮겨보면
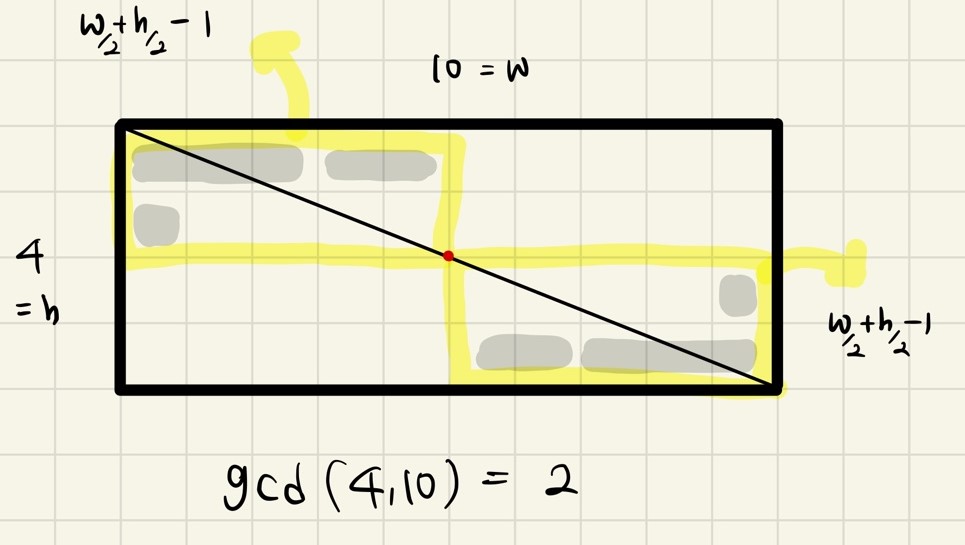
이렇게 되고 각 묶음 사각형의 회색칠된 사각형 갯수를 계산해 합쳐보면 w+h-2가 되는 것을 알 수 있다
묶음 사각형이 2개이기 때문에 w/2, h/2가 되고, -2가 붙었다.
그러면 최대 공약수가 3인 사각형의 가로, 세로가 온다면?
그렇다. 쓸 수 없는 사각형의 갯수는 w+h-2개 이다.
내가 뭐라고 하는지 모르겠지만... 모든 사각형에 적용해보면 동일하게 적용되는 것을 볼 수 있다.
최대 공약수가 1이어도 동일하게 적용된다.
정리
- math 라이브러리의 gcd 함수를 이용해 최대공약수를 구할 수 있었다.
- 이건 외우지 않는 이상 풀 수 없을 것 같다.
- 노는 게 제일 좋아 님의 블로그를 참고했다. https://luv-n-interest.tistory.com/736 더 좋은 설명
