문제
설명
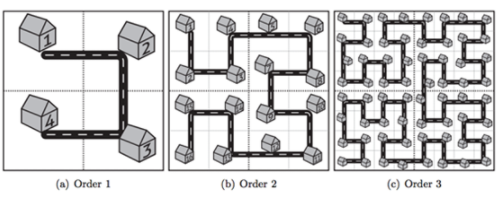
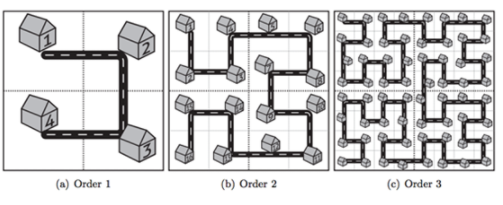
힐베르트 곡선은 다음과 같이 재귀적으로 정의된다:
∙ 1번째 힐베르트 곡선은 2 X 2 격자의 모든 점을 방문하는 곡선으로, (0, 0)에서 오른쪽/아래/왼쪽 순으로 움직인다.
∙ n ≥ 2에 대해 n번째 힐베르트 곡선은 2n X 2n 격자의 모든 점을 방문하는 곡선으로, (0, 0)에서 각 2n-1 X 2n-1 부분 격자를 오른쪽/아래/왼쪽 순으로 움직인다. 각 부분 격자를 이동하는 규칙은 다음과 같다.
좌상단 격자는 n-1번째 힐베르트 곡선을 우하향 대각선을 기준으로 대칭시킨 형태이다. 우상단 격자는 n-1번째 힐베르트 곡선이다. 하단 격자들은 상단 격자를 가로축으로 대칭한 형태로 채워져 있다.
입력
첫 번째 줄에 테스트 케이스의 수 TC가 주어진다. 이후 TC개의 테스트 케이스가 새 줄로 구분되어 주어진다. 각 테스트 케이스는 다음과 같이 구성되었다.
∙ 첫 번째 줄에 정수 n, a, b가 주어진다. n번째 힐베르트 곡선에서 a번 집과 b번 집의 거리를 계산해야 한다는 뜻이다. (1≤n≤15, 1≤a,b≤22n)
출력
각 테스트 케이스 마다 한 줄씩, 두 점 간의 거리를 미터 단위로 출력하라. 정수가 아닐 경우 가장 가까운 정수로 반올림해야 한다.
아이디어
순서가 주어졌을 때, 규칙을 따라 좌표를 표시하는 문제.
딱 봐도 재귀를 이용해서 푸는 문제긴 한데, 생각보다 접근 방법이 난해합니다.
보통 이럴때 멍청한 저는 예제를 손으로 때려넣어보곤 합니다.
편의를 위해서 집 순서를 0부터 표시하게 하였습니다.
ex1. n=3 a = 16
먼저 n=3일때 0번째집부터 63번째 집까지 있고, 16번째를 기준으로 나누면
좌상단 그리드 0,
우상단 그리드 1,
우하단 그리드 2,
좌하단 그리드 3
으로 나눠볼 수 있습니다.
16~32는 우상단 그리드 이기 때문에 y에 4를 더해주고 n=2로 넘어갑니다.
이후 문제는 n=2에서 a%16 번째 집을 찾는 문제로 바뀌게됩니다.
a = 16이라고 치면
n = 2에서 0번째 집이므로, [0,0]을 더해주어 집의 좌표값은 [0,4] 가 됩니다.
하지만 a가 0번 그리드, 3번 그리드라면 순서에 의한 좌표값이 바뀌게 됩니다.
편의를 위해 첫 n이 2라고 생각하고 접근해봅시다.
ex2-1. n = 2, a = 1
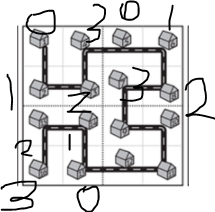
(악필 죄송 ㅎㅎ!)
0번 그리드의 1번째 집을 찾는 문제가 되었습니다.
0번 그리드임을 무시하면 1번째 집은 (0,1)이 되겠지만 실제로는 (1,0)입니다. 우상단 그리드를 표준이라 할 때, 0번 그리드에서는 x와 y의 좌표값이 바뀜을 알 수 있습니다.
ex2-2. n = 2, a = 12
3번 그리드의 0번쨰 집을 찾는 문제.
0번째 집은 표준에서는 (0,0)이지만 이 경우 (1,1)입니다.
3번 그리드에서는 (1-0,1-0)을 해주면 되겠습니다. 보다 정확히 말하면
표준에서 (x,y)라면 (1-y, 1-x) 가 됩니다.
정리
n = N에 대해서 총 집의 개수는 개이며
좌표계는 [,] 까지 있습니다.
K = 는 한 그리드에 있는 집의 수 입니다.
a번째 집을 찾을 때 a//K는 a번째 집이 위치한 그리드의 위치고,
a%K 는 n= N-1에서 새로 찾을 a가 됩니다.
만약에 n=N에서 a집의 위치가 0번째 그리드라면,
n=N-1에서 a%k집의 위치의 표준 좌표값 [x,y]를 [y,x]로 반환해주면 됩니다.
a집의 위치가 3번째 그리드라면,
먼저 x에 를 더하여 위치를 잡고,
n=N-1, a%k 집의 위치의 표준 좌표값 [x,y]를
N-1에서 최대좌표 [x_max,y_max] - [y,x]를 반환해주면 됩니다.
뭔가 혼란스럽지만 그냥 오 이게 규칙같은데? 하고 재귀를 짜본다음에
손으로 찍어본 예제를 넣어가며 검증해보면 잘 작동합니다...
구현
def coor(n,a):
if n == 0:
return [0,0]
k = 2**(2*(n-1))
tmp_anw = [0,0]
tmp_anw[0] += (a // k) // 2 * (k ** (1 / 2))
if (a//k) == 1 or a//k == 2:
tmp_anw[1] += (k**(1/2))
y = coor(n-1,a%k)
if a//k == 0:
return [tmp_anw[0]+y[1],tmp_anw[1]+y[0]]
elif a//k == 3:
return [tmp_anw[0]+(k**(1/2)-1)-y[1],tmp_anw[1]+(k**(1/2)-1)-y[0]]
else:
return [tmp_anw[0]+y[0],tmp_anw[1]+y[1]]
def dis(a,b):
return 10*((a[0]-b[0])**2 + (a[1]-b[1])**2)**(1/2)
T = int(input())
for t in range(1,1+T):
n, a, b = map(int,input().split())
# n = 1일떄 몇번째인가?
a -= 1
b -= 1
coor_a = coor(n,a)
coor_b = coor(n,b)
print(f'#{t} {round(dis(coor_a,coor_b))}')실행
입력
2 # Test Case Number
2 3 8 # N A번째 집 B번째 집
3 63 48 출력
[1.0, 1.0] [1.0, 2.0] # N=2에서 A번째 집, B번째 집 좌표
[7.0, 1.0] [7.0, 4.0]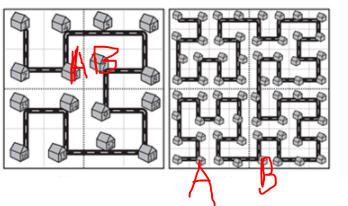
뭔가 납득은 잘 안가지만 아무튼 잘 나옵니다..
느낀 점
재귀를 짤때 n=N에서 n=0까지 재귀를 다 생각하면 머리 아픕니다.
그냥 적당한 N에서 N-1과 N 사이의 규칙을 찾아서 (점화식을 찾아서)
재귀를 구현해본 뒤 출력을 보고 틀리다면 어디서 틀리고, 어떻게 고쳐야할 지 생각해보는 편이 편한 것 같습니다.