🌈 소수 & 최대공약수
🔥 소수 구하기
🔥 골드바흐의 추측
🔥 최대공약수
1. 소수 구하기
1) O(N) 소수 구하기
- 소수는 1과 자기 자신(n)으로만 나눌 수 있기 때문에 2부터 n-1까지 숫자 중 나눠떨어지면 소수가 아님
- n은 10이라면, 1과 10으로만 떨어졌을 때가 약수이기 때문에 10을 2부터 9까지의 수로 나눠봤을 때, 나머지가 0인 경우가 1개라도 있다면 이는 소수가 아닌 것임
import sys def is_prime(n): if n <= 1: return False for i in range(2,n): if n % i == 0: return False return True # 소수 입력 n = int(sys.stdin.readline()) print(is_prime(n))
2) O(sqrt(N)) 소수 구하기
- 2부터 n-1까지 모두 나누는 것보다 (루트 n) + 1 까지의 수를 나누면 시간복잡도를 줄일 수 있음
- 루트 N을 구하기 위해서는 from math import sqrt 라이브러리 사용
- n이 9이라면, 2부터 8까지 모두 나눠볼 필요업이 나누는 범위를 2부터 루트9+1까지의 범위로 for문을 실행시키면, 2부터 3까지만 나눠보기 때문에 수행 요청이 현저히 줄어듬
import sys from math import sqrt def is_prime(n): if n <= 1: return False for i in range(2,int(sqrt(n))+1): if n % i == 0: return False return True # 소수 입력 n = int(sys.stdin.readline()) print(is_prime(n))
2) O(N log log N) 소수 구하기
- 에라토스테네스의 체
- 소수라고 판단된 수가 있다면, 이 수의 배수들은 모두 소수가 아닌 것으로 체크함
- 이런 식으로 범위 내에 모든 수를 전처리 해놓으면 O(1) 로 소수로를 구할 수 있음
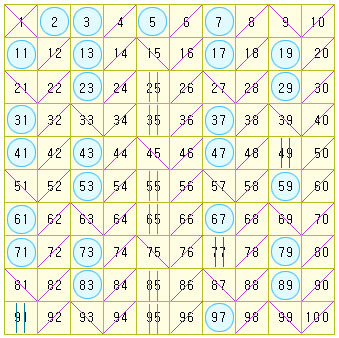
- 소수면 True, 소수가 아니면 False인 0부터 n+1까지의 범위의 배열을 먼저 만들어 둔 것은 N log log N의 시간 복잡도를 가짐
- 이후 여기서 인덱스 번호로 소수를 찾으면 O(1)의 소수 찾기가 가능함
import sys from math import sqrt # eratosthenes_sieve def eratosthenes_sieve(n): b = [True for i in range(n + 2) ] # 배열을 만들어 모두가 소수라고 가정을 해둠 b[1] = False # b[1]은 숫자 1이기 때문에 False for i in range(2, int(sqrt(n)) + 1): # n을 기준으로 루트n한 수의 왼쪽 범위 if b[i]: # i가 True라면(2,3...), for j in range(i*i, n+1, i): # n범위까지 범위 중 i의 배수를 배열에 담음 b[j] = False # i의 배수를 False로 바꿈 return b # prime def is_prime(b,n): return b[n] # 1000까지의 수 중 소수를 구해둔 배열 b = eratosthenes_sieve(1000) n = int(sys.stdin.readline()) print(is_prime(b,n))
2. 골드바흐의 추측
- 2보다 큰 모든 짝수는 두 소수의 합으로 나타낼 수 있다는 것이 골드바흐의 추측임
- 이 때, 이 두소수의 합을 나타내는 표현을 골드바흐의 파티션이라고 함
- n이 4일 때 = 소수(2) + 소수(2)
- n이 6일 때 = 소수(3) + 소수(3)
- n이 8일 때 = 소수(3) + 소수(5)
- n이 10일 때 = 소수(5) + 소수(5)
- n이 12일 때 = 소수(5) + 소수(7)
- n이 14일 때 = 소수(3) + 소수(11) & 소수(7) + 소수(7)
- 2보다 큰 짝수(n)이 주어졌을 때, n의 골드바흐 파티션을 출력하는 알고리즘 작성해보기
- 단, 14처럼 골드바흐의 파티션이 2개 이상인 경우에는 두 소수의 차이가 가장 작은 것을 출력
⇢ n이 14일 때 = 소수(7) + 소수(7)- 문제에서 n의 범위는 2보다 크고 10000이하의 짝수이기 때문에 4 <= n 10000 이고, 이 범위의 에라토스테네스의 체를 배열로 만들어 둠
from math import sqrt # eratosthenes_sieve로 10000까지의 모든 소수를 구함 def eratosthenes_sieve(n): b = [ True for i in range(n+2)] b[1] = False for i in range(2, int(sqrt(n))+1): if b[i]: for j in range(i*i, n+1, i): b[j] = False primes = [] for i in range(n+1): if b[i]: # 소수라면, primes.append(i) return primes primes = eratosthenes_sieve(10000) # 10000까지의 수 중 소수를 배열로 보관 print(primes)
- 10000 미만의 소스를 담음 primes를 만들었기 때문에, 이 배열을 i와 j로 순회하여 그 합이 n인 primes[i]와 primes[j]의 값을 구함
- 이 방법은 O(N^2) 만큼의 시간 복잡도를 가짐
import sys from math import sqrt # eratosthenes_sieve로 10000까지의 모든 소수를 구함 def eratosthenes_sieve(n): b = [ True for i in range(n+2)] b[1] = False for i in range(2, int(sqrt(n))+1): if b[i]: for j in range(i*i, n+1, i): b[j] = False primes = [] for i in range(n+1): if b[i]: # 소수라면, primes.append(i) return primes primes = eratosthenes_sieve(10000) # 10000까지의 수 중 소수를 배열로 보관 print(primes) # 입력 T = int(sys.stdin.readline()) # Test case for tc in range(T): n = int(sys.stdin.readline()) # 2보다 큰 짝수(4 <= n < 10000) # eratosthenes_sieve를 순회하며, 더해서 n이 나오는 i와 j를 구함 for i in range(len(primes)): for j in range(len(primes)): if primes[i] + primes[j] == n: print(primes[i], primes[j])
- 시간 복잡도를 줄이기 위해, 이중탐색(binary search) 적용해봄
- 문제에서는 두 소수의 합이 n인 골드바흐의 파티션 중에서 그 차이가 작은 것을 구해야함
- 파티션인 res 리스트를 케이스 별로 만들고, 맨 처음 찾은 두 소수를 res에 넣음
- 이후에 찾게되는 골드바흐의 파티션은 abs 함수로 그 차이가 작을 때만, res 값을 교체시킴
import sys from math import sqrt # eratosthenes_sieve로 10000까지의 모든 소수를 구함 def eratosthenes_sieve(n): b = [ True for i in range(n+2)] b[1] = False for i in range(2, int(sqrt(n))+1): if b[i]: for j in range(i*i, n+1, i): b[j] = False primes = [] for i in range(n+1): if b[i]: # 소수라면, primes.append(i) return primes primes = eratosthenes_sieve(10000) # 10000까지의 수 중 소수를 배열로 보관 # print(primes) # binary search def bs(l, v): le = 0 ri = len(l) - 1 while le <= ri: mid = (le+ri) // 2 if l[mid] == v: return True elif l[mid] < v: le = mid + 1 else: ri = mid - 1 return False # 입력 T = int(sys.stdin.readline()) # Test case for tc in range(T): res = [] # 매번 테스트마다 리스트를 만듬 n = int(sys.stdin.readline()) # 2보다 큰 짝수(4 <= n < 10000) # eratosthenes_sieve # binary search 적용 version => O(N * log N) for i in range(len(primes)): if bs(primes, n-primes[i]): if len(res) == 0: # res가 비어있을 때만 처음 찾은 두 소수의 값을 넣음 res = [primes[i], n - primes[i]] else: # 이미 1개를 찾았을 때는 그 차이를 비교해서 차이가 작은 것을 찾음 if abs(res[0]-res[1]) > abs(primes[i]-(n-primes[i])): res = [primes[i], n-primes[i]] print(res[0], res[1])
3. 최대공약수
1) O(N) 최대공약수 구하기
- 약수 중에 공통된 것을 공약수라 부르고, 그 공약수 중에 가장 큰 수를 최대공약수라 함
- 정수 a,b가 1071, 1029일 때, 이 각 각의 수를 공통으로 나눌수 있는 약수 중에 가장 큰 수를 구하면됨
- 1071과 1029중 작은 수인 1071을 기준으로 2부터 순회해줘야지 공통인 약수를 구할 수 있음
- for문은 2부터 순차적으로 증가하기 때문에 ans변수에 계속 교체해주면 가장 큰 약수인 최대공약수를 ans가 갖고 있음
def gcd(a,b): ans = None for i in range(2, min(a,b)): if a % i == 0 and b % i == 0: ans = i return ans print(gcd(1071, 1029))
2) O(log N) 최대공약수 구하기
- O(log N)의 시간복잡도로 최대공약수를 구하기 위해서는 유클리드 호제법 사용
- 정수 a,b가 주어졌을 때, 최대 공약수를 구하기 위해서 a를 b로 나눈 나머지(r)를 구한 뒤, b를 다시 그 나머지로 나눠주는 과정을 반복함
- b를 계속 r로 나눌 때, 나머지가 0이 된다면 그 때 b값이 최대 공약수가 되는 것이 유클리드 호제법임
def gcd(a,b): r = a % b while r: # r이 0이되기 전까지 반복 a = b b = r r = a % b return b print(gcd(1071, 1029))
- 재귀함수를 사용하여 간결하게 표현하기
- gcd(1071, 1029) ⇢ gcd(1029, 42) ⇢ gcd(42, 21) ⇢ gcd(21, 0) = 21
def gcd(a,b): if b: # b가 0이 아니라면, return gcd(b, a%b) return a print(gcd(1071, 1029))
- 삼항연산자로 더 간결하게 표현
def gcd(a,b): return gcd(b, a%b) if b else a print(gcd(1071, 1029))
3) BOJ #9613 : GCD 합
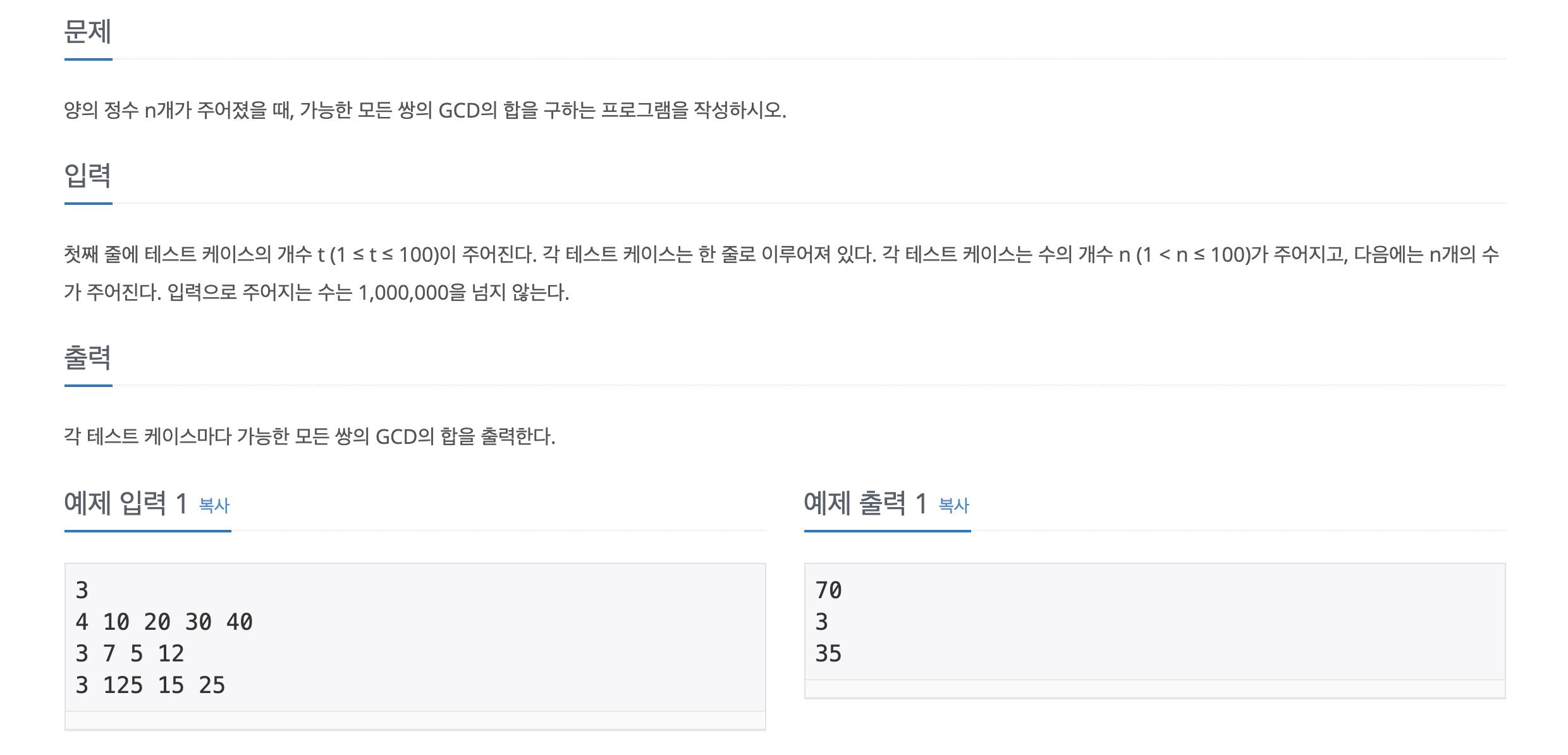
- 테스트 케이스 T를 받은 뒤, 케이스만큼 정수 n개를 리스트로 받음
- 첫번째 정수는 리스트의 요소수인 n이고, 이를 제외한 정수 n개의 리스트의 모든 정수 쌍을 만듬
- 정수 쌍의 GCD에 투입시킨 뒤, 이를 모두 더함
import sys # GCD 유클리드 호제법 def gcd(a,b): return gcd(b,a%b) if b else a # 입력 T = int(sys.stdin.readline()) for tc in range(T): l = list(map(int, sys.stdin.readline().split())) n = l[0] # list의 요소수 l = l[1:] # n개의 정수 list # print(n, l) # n개의 정수 리스트의 모든 쌍 집합 ans = 0 for i in range(len(l)-1): for j in range(i + 1, len(l)): ans = ans + gcd(l[i], l[j]) print(ans) # 모든 쌍을 구하는 for문의 과정 # l = [10 20 30 40] # for i in range(len(l)-1)의 i범위는 0,1,2 # for j in range(i + 1, len(l)) 의 j범위는 1,2,3,4 # i = 0일 때, j는 1,2,3 / gcd(10,20), gcd(10,30), gcd(10,40) # i = 1일 때, j는 2,3 / gcd(20,30), gcd(20,40) # i = 2일 때, j는 3 / gcd(30,40)
Keep Going, Keep Coding!