알고리즘 기초 - 시간 복잡도

🌈 시간 복잡도

🔥 시간 복잡도란?

🔥 Big O notation

🔥 시간 복잡도 고려한 문제 풀이 예시

1. 시간 복잡도란?

• 알고리즘 문제에서 실행 시간은 계산량(계산 횟수)와 비례하고, 이 계산량을 order라함
• 이에 계산 횟수가 많은 문제 풀이 방법은 그만큼 실행 시간이 길어지기 때문에 시간 복잡도에서 불리함
• 일반적으로 알고리즘 문제에서 경우의 수가 10의 8승이면, 1초 정도 소요되는 것으로 고려하고, 이를 기준으로 시간 복잡도를 계산함
• 🔍 시간 복잡도 : 10의 8승 = 1억 = 1초

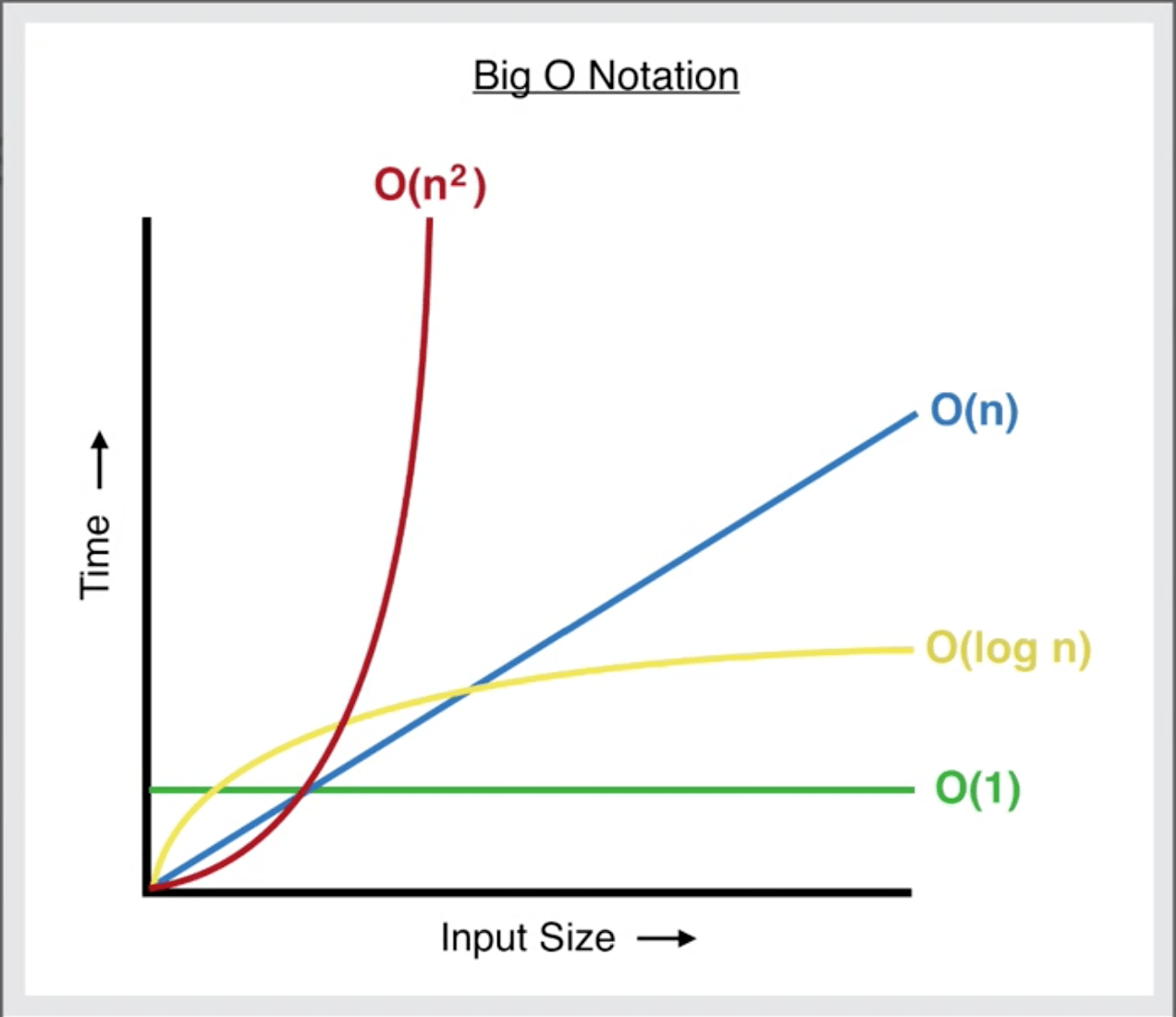
2. Big O notation

• Big O notation은 점근적 상한에 대한 표기법으로 입력이 굉장히 크다고 가정했을 때, 최악의 경우 계산되는 계산량을 의미
• 예를 들어, 입력의 크기인 N이 어마하게 크다고 가정했을 때, N보다 N 제곱의 값이 큼
• 또한 입력의 크기인 N이 어마하게 크다고 가정했을 때, Log N보다는 N이 클 수 밖에 없음
  
• 작성한 코드의 계산량이 9*N^2 + 2*N + k이면 Big O noation 표기법에 따라 O(9*N^2 + 2*N + k)로 표현할 수 있는데, 9*N^2이 엄청 큰 수이기 때문에 상대적으로 2*N + k는 무시해도 될 숫자임
• 즉, 가장 큰 차수를 제외하고 나머지를 버릴 경우, O(9*N^2 + 2*N + k)는 O(9*N^2)로 고려
• 따라서, 시간 복잡도를 Big O notation으로 표기한다는 것은 입력에 따른 계산량을 최고차수만 남기는 것임(상수도 제외 가능)
• Big O notation 표기 예시
  • 🔍 O(5*N^3 + 99*N^2 + k) = O(N^3)
  • 🔍 O(3^N + N^3 + N+1) = O(2^N)
  • 🔍 O(123810847014) = O(1)

• 1부터 n까지의 합을 구하는 알고리즘 Big O 구하기

# 풀이 1 / Big O : O(n)
# n만큼 반복되기 때문에 O(n) 만큼의 복잡도가 발생
def sum_all(n):
    total = 0
    for i in range(1, n+1):
        total += i
    return total

# 풀이 2(가우스 덧셈) / Big O : O(1)
# 바로 계산되기 때문에 O(1)만큼의 복잡도가 발생
def sum_all(n):
    return int(n*(n+1)/2)

• 두번째 풀이 방법인 가우스 덧셈이 성능이 더 좋음

3. 시간 복잡도 고려한 문제 풀이 예시

• n 개의 오름차순 정수로 이루어진 리스트가 주어졌을 때, k가 존재하면 1, 존재하지 않으면 0을 출력
• n의 범위는 1<= n < 1,000,000,000 이고, k의 범위는 1 <= k < 1,000,000일 때를 가정하면, O(10^9)이기 때문에 10초가 소요됨
• 이럴 경우, 선형 검색(선형 탐색)으로 풀면 시간 초과가 발생하기 때문에 이진 검색(이진 탐색)을 사용하여 코드를 작성해야 함

✍🏻 선형 탐색으로 풀 때

import sys
n, k  = map(int, sys.stdin.readline().split())
l = list(map(int, sys.stdin.readline().split()))
found = False
for i in range(len(l)):
    print(l[i])
    if l[i]  == k:
        found = True
# for문이 종료된 뒤에 found 값을 평가
if found:
    print(1)
else:
    print(0)

✍🏻 이진 탐색으로 풀 때

import sys
n, k  = map(int, sys.stdin.readline().split())
l = list(map(int, sys.stdin.readline().split()))
found = False
left = 0
right = len(l) - 1
while left <= right:
    mid = (left + right) // 2 # 몫만 필요
    if l[mid] == k:
        found = True
        break
    elif l[mid] < k: # 중간값이 k보다 작으면 탐색 범위 중 앞 쪽 절반을 버림
        left = mid + 1
    elif l[mid] > k: # 중간값이 k보다 작으면 탐색 범위 중 뒤 쪽 절반을 버림
        right = mid - 1
if found:
    print(1)
else:
    print(0)

• 숫자가 적혀있는 N장의 종이가 담긴 상자에서 종이를 4번 뽑아 총 합이 m이면 승리한다. 승리할 수 있으면 1, 아니면 0을 출력하시오.(1 <= N < 1,000, 1<= m < 10^8, 1 <= K_i < 10^8)

✍🏻 풀이1 => 시간초과 : O(10^10)

import sys
n, m = map(int, sys.stdin.readline().split())
box = list(map(int, sys.stdin.readline().split()))
box.sort() # binaray search하기 위해 정렬
# 배열(box)에 target(m-s)이 존재하는지 binaray search로 확인
def binary_search(box, target):
  left = 0
  right = len(box) - 1
  while left <= right:
    mid = (left + right) // 2
    if box[mid] == target:
      return True
    elif box[mid] < target:
      left = mid + 1
    elif box[mid] > target:
      right = mid - 1
  return False
# m에서 3개의 숫자의 총합인 s를 뺀 값이 존재하는지 확인
# (m-s) + s = m      
res = 0
for i in range(n):
  for j in range(n):
    for k in range(n):
      s = box[i] + box[j] + box[k]
      if binary_search(box, m-s):
        res = 1
print(res)

✍🏻 풀이2

import sys
n,m = map(int, sys.stdin.readline().split())
box = list(map(int, sys.stdin.readline().split()))
box.sort()
def binaray_search(box, target):
    left = 0
    right = len(box) - 1
    while left <= right:
        mid = (left + right) // 2
        if box[mid] == target:
            return True
        elif box[mid] < target:
            left = mid + 1
        else:
            right = mid - 1
    return False
# N^3 log N => N^2 log N
# N^2, N^2로 둘로 나눔
n2l = []
for i in range(n):
    for j in range(n):
        n2l.append(box[i] + box[j])
result = 0
n2l.sort()
for i in range(len(n2l)):
     if binaray_search(n2l, m - n2l[i]):
         result = 1
print(result)