알고리즘 기초 - 힙(Heap) 자료구조

ID짱재·2021년 5월 31일
algorithm
0

Algorithm

목록 보기
10/20
post-thumbnail

🌈 힙(Heap)

🔥 힙(Heap) 이란?

🔥 이진 탐색 트리와 heap의 공통점과 차이점

🔥 heap에 데이터 삽입

🔥 heap에 데이터 삭제

🔥 heap 연습 문제


1.힙(Heap) 이란?

  • heap은 최대값과 최소값을 빠르게 찾기 위해 고안된 완전 이진 트리(Complete Binary Tree)
  • 배열에 데이터를 넣고, 최대값과 최소값을 찾으려면 O(n)의 시간 복잡도가 소요되지만, heap에서 최대값과 최소값을 찾을 때 시간복잡도는 O(logN)임
  • 즉, 우선순위 큐와 같이 최대값 또는 최소값을 빠르게 찾아야할 때 heap이 활용됨
  • heap은 최대값을 구하기 위한 구조 Max heap(최대 힙)과 최소값을 구하기 위한 Min heap(최소 힙)으로 구분됨
  • heap은 다음과 같이 두 가지 조건을 가지고 있는 자료구조임
    • Parent 노드의 값은 언제나 Child 노드가 가진 값보다 같거나 크다.(최대 힙 일 경우)
      • 최소힙은 맨 위의 Node의 값이 가장 작아지고, 최대힙은 맨 위의 Node의 값이 가장 큼
    • 완전 이진 트리 형태를 가짐

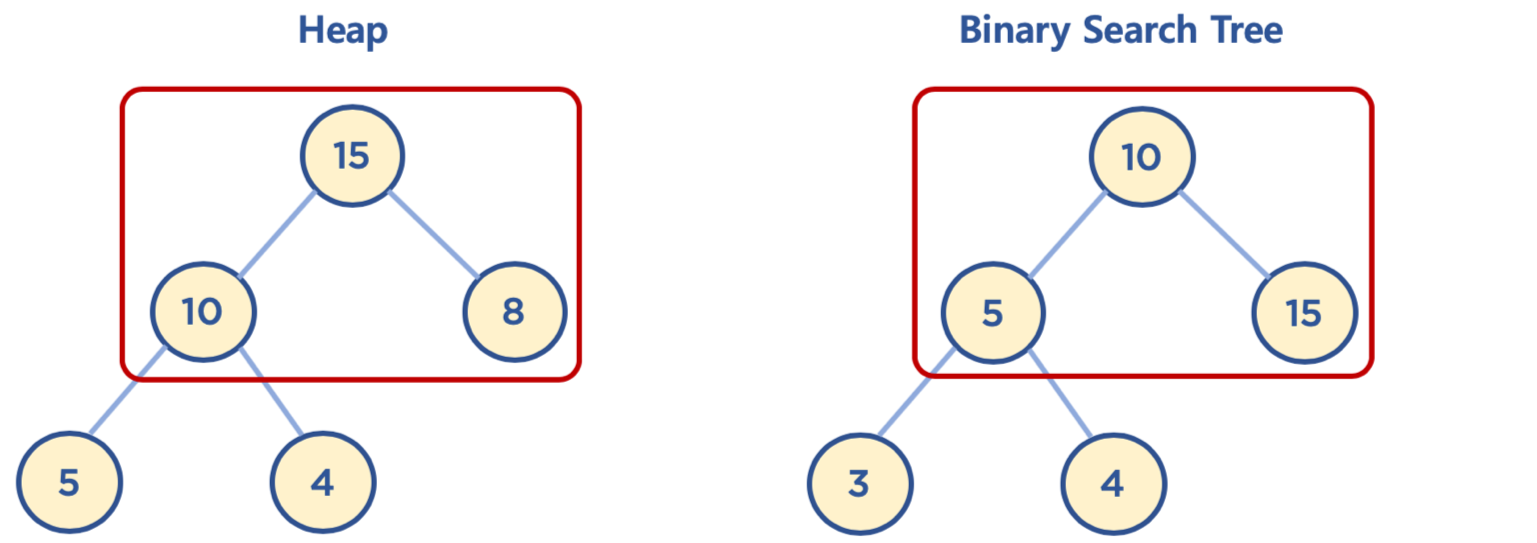
2. 이진 탐색 트리와 heap(완전 이진 트리)의 공통점과 차이점

1) 공통점

  • heap과 이진 탐색 트리는 모두 이진 트리임

2) 차이점

  • heap은 각 노드의 값이 자식 노드 보다 크거나 같음(Max heap일 경우)
  • 이진 탐색 트리는 왼쪽 자식 노드의 값이 가장 작고, 그 다음으로는 부모 노드 값이 작고, 오른쪽 자식 노드의 값이 가장 큼
    • 부모 노드의 값과 비교해서 작으면 왼쪽, 크면 오른쪽에 삽입하기 때문
  • heap은 이진 탐색 트리의 조건인 자식 노드에서 작은 값은 왼쪽, 큰 값은 오른쪽이라는 조건 없음
    • 크기를 비교하지 않고, 이진 형태를 띄도록 왼쪽부터 값을 삽입함
  • 서로 목적이 다름
    • 이진 탐색 트리는 탐색을 위한 구조, 힙은 최대/최소값 검색을 위한 구조 중 하나로 이해하면 됨

3. heap에 데이터 삽입

  • 힙은 완전 이진 트리이므로, 첫 데이터가 삽입되면 Root Node가 됨
  • 추가로 데이터가 삽입되면, 왼쪽 Node가 있는지 판단하여 없으면 왼쪽 Node에 넣고, 인쪽 Node가 이미 있다면 오른쪽 Node를 탐색하여 없으면 넣음
  • 오른쪽 Node까지 있다면, 다시 왼쪽 Node의 자식들이 존재하는지를 확인하여 왼쪽부터 삽입함
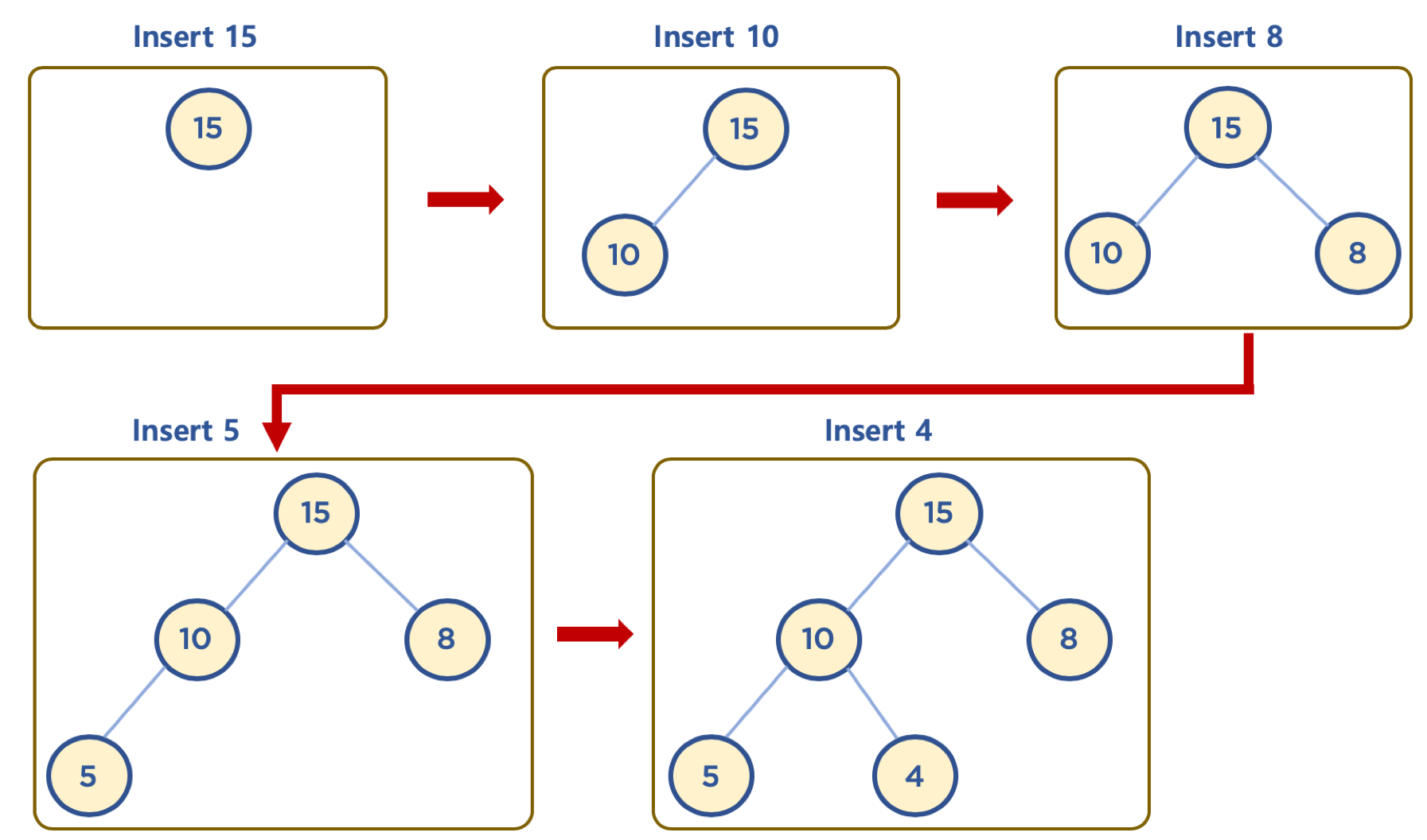
  • Swap의 방법은 삽입시킨 Node의 값과 부모 Node의 값을 비교하여 삽입한 Node의 값이 더 크다면 크지 않을 때 까지 계속 Swap을 진행(Max Heap의 경우)
  • 즉, 완전 이진 트리의 규칙 대로 왼쪽부터 자리를 잡게한 뒤, 삽입된 위치에서 자신의 값과 부모 Node의 값을 비교해 Swap함
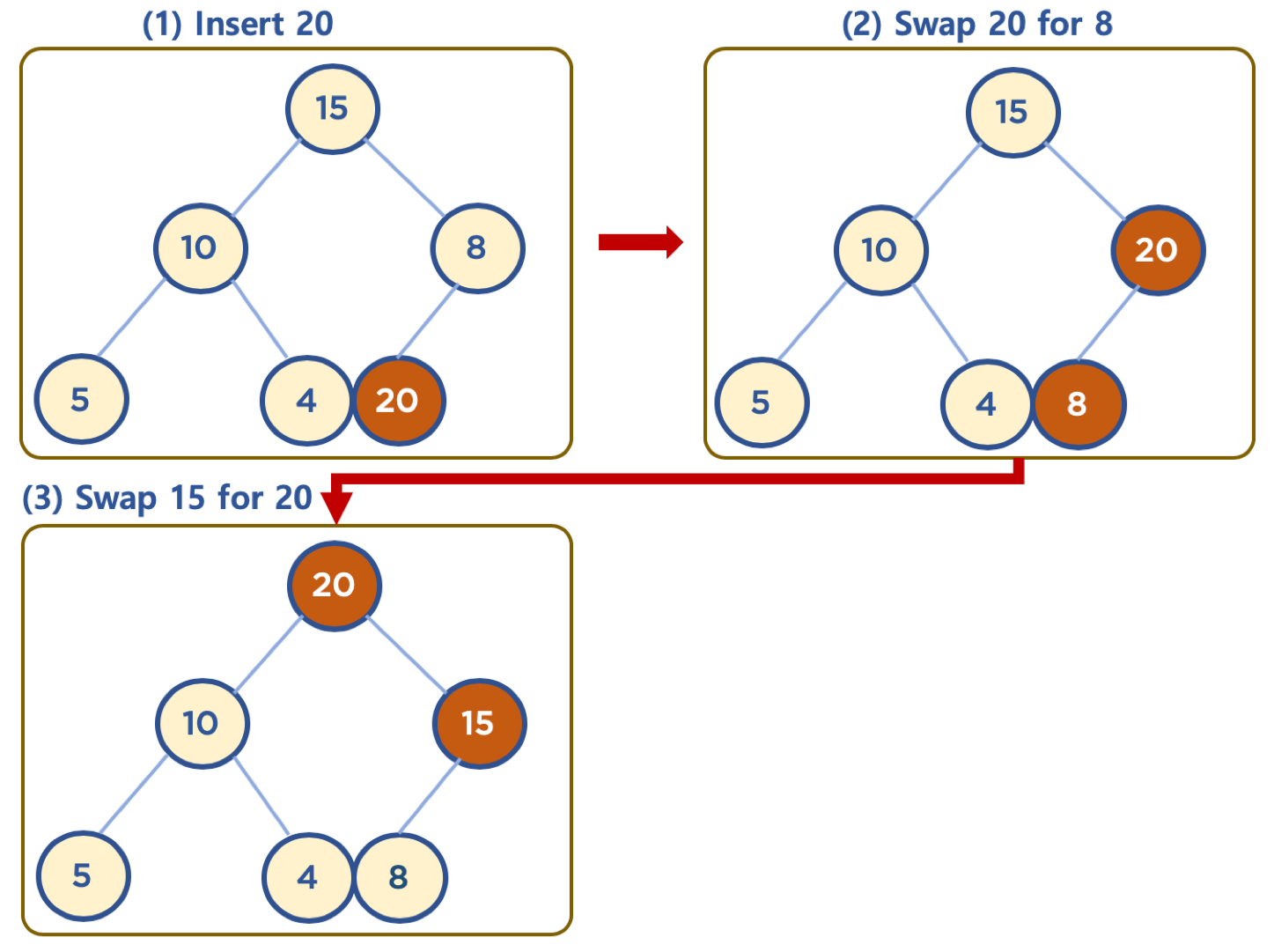
  • 일반적으로 힙 구현 시, 배열을 활용하는데 heap 구현의 편의를 위해 Root Node 인덱스 번호를 1로 지정하면 구현이 보다 수월함(0번 index를 비움)
    • 부모 Node 인덱스 번호는 자식 Node 인덱스를 2로 나눈 몫과 같음
      🔍 parent node's index = child node's index // 2
    • 왼쪽 자식 Node 인덱스 번호는 부모 Node 인덱스 번호에 2를 곱한 것과 같음
      🔍 left child node's index = parent node's index * 2
    • 오른쪽 자식 Node 인덱스 번호는 부모 Node 인덱스 번호에 2를 곱한 뒤 + 1 한 것과 같음
      🔍 right child node's index = (parent node's index * 2) + 1
# heap 데이터 삽입
class Heap:
    def __init__(self, data):
        self.heap_array = list()
        self.heap_array.append(None) # 맨 앞에 요소는 None으로 채움
        self.heap_array.append(data)
    def move_up(self, inserted_idx):
        if inserted_idx <= 1: # inserted_idx가 Root Node일 경우
            return False
        parent_idx = inserted_idx // 2
        # inset한 Node의 값이 insert한 Node의 parent의 Data값 비교
        if self.heap_array[inserted_idx] > self.heap_array[parent_idx]:
            return True
        else:
            return False
    # 완전 이진트리의 규칙으로 배열에 Node 값 삽입
    def insert(self, data):
        if len(self.heap_array) == 0:
            self.heap_array.append(None)
            self.heap_array.append(data)
            return True
        self.heap_array.append(data)
        # Swap
        inserted_idx = len(self.heap_array) - 1 # 최근 추가된 데이터의 index 번호
        # move_up 매서드에 inserted_idx값을 전달하였을 때, True가 return되면 계속 반복
        while self.move_up(inserted_idx): 
            parent_idx = inserted_idx // 2
            self.heap_array[inserted_idx], self.heap_array[parent_idx] = self.heap_array[parent_idx], self.heap_array[inserted_idx] # swap
            inserted_idx = parent_idx
        return True
# 데이터 삽입 확인        
heap = Heap(15)
print(heap.heap_array) # [None, 15]
heap.insert(10)
print(heap.heap_array) # [None, 15, 10]
heap.insert(8)
print(heap.heap_array) # [None, 15, 10, 8]
heap.insert(5)
print(heap.heap_array) # [None, 15, 10, 8, 5]
heap.insert(4)
print(heap.heap_array) # [None, 15, 10, 8, 5, 4]
heap.insert(20)
print(heap.heap_array) # [None, 20, 10, 15, 5, 4, 8]

4. heap에 데이터 삭제

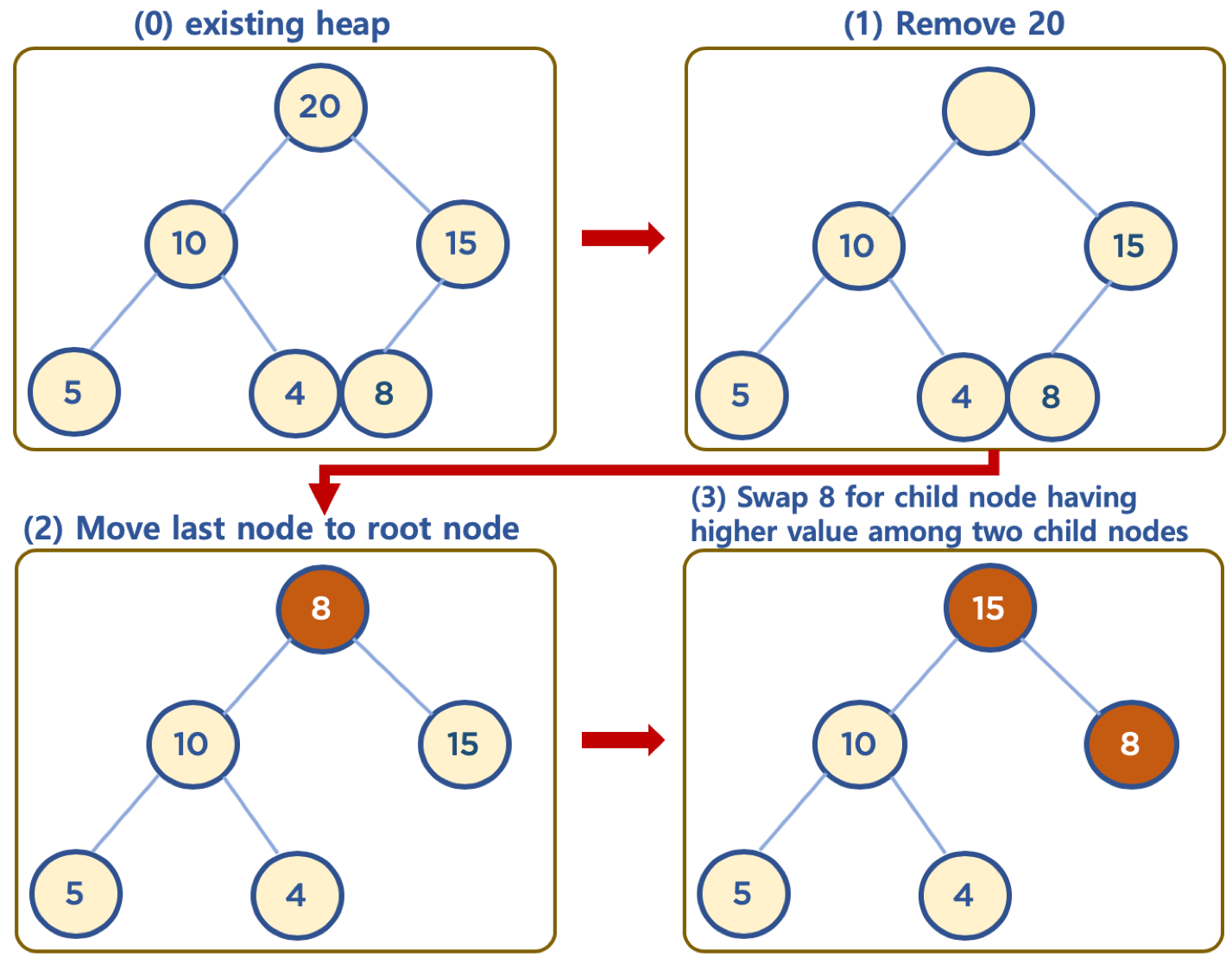
  • 일반적으로 heap에서의 삭제는 최상단 노드(Root Node)를 삭제하는 것이 일반적임
  • heap의 용도는 최대값 또는 최소값을 root에 놓고, 바로 꺼내 쓸수 있도록하는데 목적이 있기 때문
  • 이에 상단에서 데이터 삭제 시, 가장 마지막에 추가한 Node를 Root Node로 이동 시킨 뒤, Parent Node와 Child Node의 값을 비교하면서 Swap시킴
  • Swap 작업은 Root Node의 자식 Node 2개를 비교해서 더 큰 값과 Swap시킴(둘 중 큰 값을 올림)
  • 이 Swap 작업은 자식 Node가 없거나, 부모 Node가 자식 Node보다 클 때까지 처리하고, 자식 Node의 유무에 따라 3가지 경우의 수로 나뉨
    • case1 : 왼쪽 자식 노드가 없을때(자식 Node가 모두 없다는 의미)
    • csee2 : 왼쪽 자식 노드만 있을 때(오른쪽 자식 노드는 없음)
    • csee3 : 왼쪽, 오른쪽 자식 노드가 모두 있을 때
# heap 데이터 삭제
class Heap:
    def __init__(self, data):
        self.heap_array = list()
        self.heap_array.append(None)
        self.heap_array.append(data)
    def move_up(self, inserted_idx):
        if inserted_idx <= 1: # inseted_inx가 Root Node일 경우
            return False
        parent_idx = inserted_idx // 2
        # inset한 Node의 값이 inset한 Node의 parent의 Data값 비교
        if self.heap_array[inserted_idx] > self.heap_array[parent_idx]:
            return True
        else:
            return False
    # 완전 이진트리의 규칙으로 배열에 Node 값 삽입
    def insert(self, data):
        if len(self.heap_array) == 0:
            self.heap_array.append(None)
            self.heap_array.append(data)
            return True
        self.heap_array.append(data)
        # Swap
        inserted_idx = len(self.heap_array) - 1 # 최근 추가된 데이터의 index 번호
        # move_up 매서드에 inserted_idx값을 전달하였을 때, True가 return되면 계속 반복
        while self.move_up(inserted_idx): 
            parent_idx = inserted_idx // 2
            self.heap_array[inserted_idx], self.heap_array[parent_idx] = self.heap_array[parent_idx], self.heap_array[inserted_idx] # swap
            inserted_idx = parent_idx
        return True
    # Root Node 삭제
    def move_down(self, poped_idx):
        left_child_poped_idx = poped_idx * 2
        right_child_poped_idx = poped_idx * 2 + 1
        # case1 : 왼쪽 자식 노드가 없을때(자식 Node가 모두 없다는 의미)
        if left_child_poped_idx >= len(self.heap_array):
            return False
        # csee2 : 왼쪽 자식 노드만 있을 때(오른쪽 자식 노드는 없음)
        elif right_child_poped_idx >= len(self.heap_array):
            if self.heap_array[poped_idx] < self.heap_array[left_child_poped_idx]:
                return True # 자식이 더 클 때는 Swap(While문 실행)
            else:
                return False
        # csee3 : 왼쪽, 오른쪽 자식 노드가 모두 있을 때
        else:
            if self.heap_array[left_child_poped_idx] > self.heap_array[right_child_poped_idx]:
                if self.heap_array[poped_idx] < self.heap_array[left_child_poped_idx]:
                    return True
                else:
                    return False
            if self.heap_array[left_child_poped_idx] < self.heap_array[right_child_poped_idx]:
                if self.heap_array[poped_idx] < self.heap_array[right_child_poped_idx]:
                    return True
                else:
                    return False
    def pop(self):
        # Node가 없거나(비어있는 이진 트리), Root Node만 있는 경우
        if len(self.heap_array) <= 1: 
            return None
        returned_data = self.heap_array[1] # 첫번째 Node의 값(Root Node의 value)
        # Swap
        self.heap_array[1] = self.heap_array[-1] # 마지막 데이터를 Root Node로 교체
        del self.heap_array[-1] # Root Node로 이동했기 때문에 삭제
        poped_idx = 1
        while self.move_down(poped_idx): # move_down 메서드를 통해 True를 반환 받으면 반복문 실행
            left_child_poped_idx = poped_idx * 2
            right_child_poped_idx = poped_idx * 2 + 1
            # csee2 : 왼쪽 자식 노드가 있을 때
            if right_child_poped_idx >= len(self.heap_array):
                if self.heap_array[poped_idx] < self.heap_array[left_child_poped_idx]:
                    self.heap_array[poped_idx], self.heap_array[left_child_poped_idx] = self.heap_array[left_child_poped_idx], self.heap_array[poped_idx]
                    poped_idx = left_child_poped_idx
            # csee3 : 왼쪽, 오른쪽 자식 노드가 모두 있을 때
            else:
                if self.heap_array[left_child_poped_idx] > self.heap_array[right_child_poped_idx]:
                    if self.heap_array[poped_idx] < self.heap_array[left_child_poped_idx]:
                        self.heap_array[poped_idx], self.heap_array[left_child_poped_idx] = self.heap_array[left_child_poped_idx], self.heap_array[poped_idx]
                if self.heap_array[left_child_poped_idx] < self.heap_array[right_child_poped_idx]:
                    if self.heap_array[poped_idx] < self.heap_array[right_child_poped_idx]:
                        self.heap_array[poped_idx], self.heap_array[right_child_poped_idx] = self.heap_array[right_child_poped_idx], self.heap_array[poped_idx]
        return returned_data
# 데이터 삽입 확인        
heap = Heap(15)
heap.insert(10)
heap.insert(8)
heap.insert(5)
heap.insert(4)
print(heap.heap_array) # [None, 15, 10, 8, 5, 4]
heap.insert(20)
print(heap.heap_array) # [None, 20, 10, 15, 5, 4, 8]
# 데이터 삭제 확인
heap.pop()
print(heap.heap_array) # [None, 15, 10, 8, 5, 4]
heap.pop()
print(heap.heap_array) # [None, 10, 4, 8, 5]
heap.pop()
print(heap.heap_array) # [None, 8, 4, 5]

5. heap 연습 문제

1) BOJ 1715 : 카드 정렬하기(https://www.acmicpc.net/problem/1715)

  • PriorityQueue는 put()으로 삽입하고, get()으로 추출할 수 있는 Heap 자료 구조를 위한 라이브러리임
  • PriorityQueue을 사용하면, 자료 중 가장 작은 것 부터 순서데로 꺼내올 수 있음
import sys
from queue import PriorityQueue
pq = PriorityQueue()
# 삽입 : put()
pq.put(200)
pq.put(1)
pq.put(20)
pq.put(300)
pq.put(90)
pq.put(8)
pq.put(33)
# 추출 : get()
for i in range(pq.qsize()):
    print(pq.get())
"""
1
8
20
33
90
200
300
"""
  • 이에 가장 작은 2개의 카드 수를 추출한 뒤, 이를 더해서 다시 PriorityQueue에 넣는 작업을 PriorityQueue가 비어있을 때 까지 반복함
  • PriorityQueue는 len()을 사용할 수 없기 때문에 PriorityQueue 비어있을 때 까지 반복하기 위해 qsize() 함수를 사용
  • 또한 출력값은 가장 작은 2개의 수를 추출하여 더한 값을 계속 ans 변수에 더함으로써 마지막에 출력
# Heap
# BOJ 1715 : 카드 정렬하기
import sys
from queue import PriorityQueue
n = int(sys.stdin.readline())
pq = PriorityQueue()
for i in range(n):
    a = int(sys.stdin.readline())
    pq.put(a)
ans = 0
while pq.qsize() > 1:
    min1 = pq.get() # 가장 작은 것
    min2 = pq.get() # 그 다음 작은 것
    next = min1 + min2 
    ans += next
    pq.put(next) # 다시 넣음
print(ans)
profile
ID짱재
Keep Going, Keep Coding!
이전 포스트

알고리즘 기초 - 이진 탐색 트리(Binary Search Tree)

다음 포스트

알고리즘 기초 - 정렬 알고리즘(Sort Algorithm)

0개의 댓글