1. 꼭 필요한 자료구조 기초
탐색이란 많은 양의 데이터 중에서 원하는 데이터를 찾는 과정을 의미한다. 프로그래밍에서는 그래프, 트리 등의 자료구조 안에서 탐색을 하는 문제를 자주 다룬다. 대표적인 탐색 알고리즘으로 DFS와 BFS를 꼽을 수 있는데 이 두 알고리즘의 원리를 제대로 이해해야 코딩 테스트의 탐색 문제 유형을 풀 수 있다. DFS와 BFS를 제대로 이해하려면 기본 자료구조인 스택과 큐에 대한 이해가 필요하다
자료구조란 데이터를 표현하고 관리하고 처리하기 위한 구조를 의미한다. 그중 스택과 큐는 자료구조의 기초 개념으로 다음의 두 핵심적인 함수로 구성된다.
삽입(push) : 데이터를 삽입한다.
삭제(pop) : 데이터를 삭제한다.
스택
스택은 박스 쌓기에 비유할 수 있다. 후입선출 구조이다.
stack = []
stack.append(5)
stack.append(3)
stack.pop()
print(stack)
# --> [5]파이썬에서 스택을 이용할 때에는 별도의 라이브러리를 사용할 필요가 없다. 기본 리스트에서 append(), pop() 메서드를 이용하면 스택 자료구조와 동일하게 동작한다.
큐
큐는 대기 줄에 비유할 수 있다. 선입선출 구조이다.
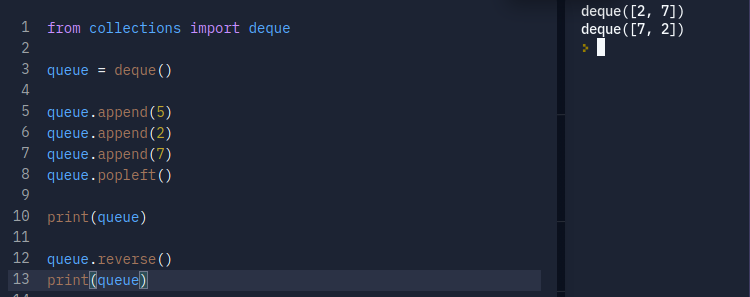
파이썬으로 큐를 구현할 때는 collections 모듈에서 제공하는 deque 자료구조를 활용하자. deque는 스택과 큐의 장점을 모두 채택한 것인데 데이터를 넣고 빼는 속도가 리스트 자료형에 비해 효율적이며 queue 라이브러리를 이용하는 것보다 더 간단하다. 또한 코테에서 collections 모듈과 같은 기본 라이브러리 사용을 허용하므로 안심해도 좋다.
이 deque 객체를 리스트화 하고 싶다면 위의 소스코드에서는 list(queue)를 진행하면 된다.
재귀함수
DFS, BFS를 구현하려면 재귀 함수도 이해하고 있어야 한다. 재귀함수 Recursive Function - 자기 자신을 다시 호출하는 함수를 의미한다.
재귀의 최대 깊이를 초과하게 되면 오류가 난다. 무한대로 재귀 호출을 진행할 수는 없다.
재귀 함수의 종료 조건
재귀 함수를 문제 풀이에서 사용할 때는 재귀 함수가 언제 끝날지, 종료 조건을 꼭명시해야 한다. 자칫 종료 조건을 명시하지 않으면 함수가 무한 호출 될 수 있다.
DFS
DFS는 Depth-First-Search깊이 우선 탐색이라고도 부르며, 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘 이다.
DFS를 설명하기 전에 먼저 그래프의 기본 구조를 알아야 한다. 그래프는 노드와 간선으로 표현되며 이때 노드를 정점이라고도 한다. 그래프 탐색이란 하나의 노드를 시작으로 다수의 노드를 방문하는 것을 말한다. 또한 두 노드를 시작으로 다수의 노드를 방문하는 것을 말한다. 또한 두 노드가 간선으로 연결되어 있다면 두 노드는 인접하다 라고 표현 한다.
프로그래밍에서 그래프는 크게 2가지 방식으로 표현할 수 있는데 코테에서는 두 방식 모두 필요하니 두 개념에 대해 바르게 알고 있어야한다.
인접 행렬 : 2차원 배열로 그래프의 연결 관계를 표현하는 방식
인접 리스트 : 리스트로 그래프의 연결 관계를 표현하는 방식
comment) 이 부분은 이해하기 힘들었다. 내가 직관적으로 이해한 방식으로 작성하였다.
인접 행렬)
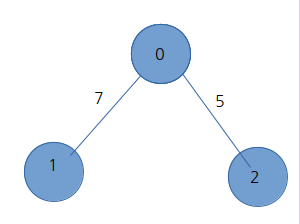
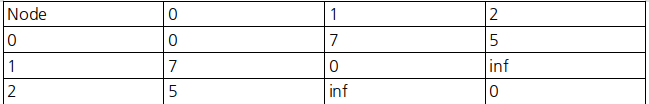
위의 표를 이해하면 코드를 이해하기 쉬울 것 같다.
INF = 987654321
graph =[
[0,7,5],
[7,0,INF],
[5,INF,0]
]
print(graph)노드 1과 2는 연결되어 있지 않기 때문에 inf 이다.
인접 리스트)
인접 리스트는 연결된 노드의 정보만 저장한다
graph = [[] for _ in range(3)]
graph[0].append((1,7))
graph[0].append((2,5))
graph[1].append((0,7))
graph[2].append((0,5))
print(graph)튜플은 (노드,거리)로 저장된다. 거리는 간선에 써진 값인데 왜 표현하는 지는 아직까진 모르겠다.
일단 두 방식은 차이가 있다. 인접 행렬 방식은 모든 관계를 저장하므로 노드 개수가 많을 수록 메모리가 불필요하게 낭비된다. 반면에 인접 리스트 방식은 연결된 정보만을 저장하기 때문에 메모리를 효율적으로 사용한다. 하지만 인접 리스트 방식은 인접 행렬 방식에 비해 특정한 두 노드가 연결되어 있는지에 대한 정보를 얻는 속도가 느리다. 연결된 데이터를 하나씩 확인해야 하기 때문이다. 특정 노드와 연결된 모든 인접 노드를 순회해야 하는 경우, 인접 리스트 방식이 인접 행렬 방식에 비해 메모리 공간의 낭비가 적다.
깊이 우선 탐색 알고리즘인 DFS는 스택 자료구조에 기초한다는 점에서 구현 간단. 실제 스택을 쓰지 않아도 되며 탐색을 수행함에 있어서 데이터 개수가 n이면 O(n)의 시간이 소요된다는 특징이 있다. DFS는 스택을 이용하는 알고리즘이기 때문에 실제 구현은 재귀를 사용했을 때 매우 간결하게 구현이 가능하다.
DFS 구현)
#DFS 메서드 정의
def dfs(graph, v, visited):
#현재 노드 방문 처리
visited[v] = True
print(v, end=' ')
# 현재 노드와 다른 노드를 재귀적으로 방문
for i in graph[v]:
if not visited[i]:
dfs(graph, i, visited)
# 각 노드가 연결된 정보를 리스트 자료형으로 표현
graph=[[],[2,3,8],[1,7],[1,4,5],[3,5],[3,4],[7],[2,6,8],[1,7]]
# 각 노드가 방문된 정보를 리스트 자료형으로 표현
visited = [False] * 9
dfs(graph,1,visited)BFS
BFS 알고리즘은 '너비 우선 탐색'이라는 의미를 가진다. 쉽게 말해 가까운 노드부터 탐색하는 알고리즘이다. DFS는 최대한 멀리 있는 노드를 우선으로 탐색하는 방식으로 동작한다 했는데, BFS는 반대다. BFS는 선입선출 방식은 큐 자료구조를 이용하는 것이 정석이다. 인접한 노드를 반복적으로 큐에 넣도록 알고리즘을 작성하면 자연스럽게 먼저 들어온 것이 먼저 나가게 되어, 가까운 노드부터 탐색을 진행하게 된다.
너비 우선 탐색 알고리즘인 BFS는 큐 자료구조에 기초한다는 점에서 구현이 간단하다. deque 라이브러리를 사용하는 것이 좋으며 캄색을 수행함에 있어 O(N) 시간이 소요된다. 일반적인 경우 DFS보다 좋은 편이라는 점까지만 추가로 기억하자.
TIP) 재귀 함수로 구현하면 컴퓨터 시스템 동작 특성상 실제 프로그램의 수행시간은 느려질 수 있다. 스택 라이브러리를 이용해 시간 복잡도를 완화하는 테크닉이 필요할 때도 있다. 다만 너비 색이 깊이 탐색보다 조금 더 빠르다는 것을 알고 있자
BFS 예제)
from collections import deque
#BFS 메서드 정의
def bfs(graph, start, visited):
queue = deque([start])
visited[start] = True
# 큐가 빌 때까지 반복
while queue:
# 큐에서 하나의 원소를 뽑아 출력
v = queue.popleft()
print(v,end= ' ')
# 해당 원소와 연결된, 아직 방문하지 않은 원소들을 큐에 삽입
for i in graph[v]:
if not visited[i]:
queue.append(i)
visited[i]= True
visited = [False] * 9
# 각 노드가 연결된 정보를 리스트 자료형으로 표현
graph=[[],[2,3,8],[1,7],[1,4,5],[3,5],[3,4],[7],[2,6,8],[1,7]]
bfs(graph, 1, visited)comment)
deque는 리스트와 비슷하다. 하지만 리스트는 아니다. 클래스기 때문에 deque라는 자료형이라는 것을 잊지말자. 그리고
while queue: -> 큐가 비어있을 때까지 라는 뜻의 반복문이다 기억하자.
x,y,z = queue.popleft()
# 하나씩 뽑아 쓸수 있다.
queue.rotate(2)
# 시계방향으로 회전 2번
#[1,2,3,4] -> [3,4,1,2]위의 코드들을 구글링하다 알게 되었다. 유용하게 쓰일 것 같다.
그럼 이젠 실전 문제에 들어가보도록 하자
실전문제 음료수 얼려먹기 p.149
문제 풀다가 이해해야할 부분 일단 파이썬 변수를 함수 자체에서 변경 시킬려면 global이라는 전역변수를 설정해 주어야한다. 근데 리스트는 왜 global을 설정을 안해줘도 되는지 이해가 안간다. 구글에 파이썬 전역 리스트라고 검색하면 나온다.
책 코드
# n,m을 공백으로 구분하여 입력받기
n,m = map(int,input().split())
# 2차원 리스트의 맵 정보 입력 받기
graph = []
for i in range(n):
graph.append(list(map(int,input())))
#dfs로 특정한 노드를 방문한 뒤에 연결된 모든 노드들도 방문
def dfs(x,y):
if x <= -1 or y <= -1 or x >=n or y >= m:
return False
if graph[x][y] == 0:
#해당 노드 방문처리
graph[x][y] = 1
#상화좌우 재귀적 방문처리
dfs(x-1,y)
dfs(x,y-1)
dfs(x+1,y)
dfs(x,y+1)
return True
return False
result = 0
for i in range(n):
for j in range(m):
if dfs(i,j) == True:
result += 1
print(result) comment) 문제 보자마자 개발자를 해먹기 틀려먹었다 생각했다.
계속 복습하고 새로운 문제를 많이 풀어봐야할 것 같다.
- 일단 이해가 안갔던 부분은 global없이 graph 리스트를 수정한 것인데 이 부분은 뮤터블과 이뮤터블을 공부를 해야할 것 같다.
이글을 보면 될것 같다.
Python은 크게 2가지 종류의 객체가 있다.
1.immutable
bool
int
float
str
tuple
2.mutable
list
dict
set
immutable은 똑같은 값의 두 변수를 선언하면,
두 변수가 같은 객체를 가리킨다.
immutable은 = 연산자를 사용하여 값을 변경하려 할 때마다,
새로운 객체를 생성해서 재할당한다.
가장 큰 차이점은,
mutable은 indexing, slicing등으로,
재할당하지 않고 값을 변경할 수 있다.
mutable는 똑같은 값의 두 변수를 선언하면,
두 변수가 다른 객체를 가리킨다.
(이는 mutable이라서 언제든 바뀔 수 있어서 그런 것 같다.)
그래서, 이 글에서 가장 중요한 점은 다음 내용인 …
Python call by referencePermalink
Python에서 함수에 파라미터로 객체를 넘기게 되면(parameter passing),
해당 local 변수가 넘겨준 global 변수가 가리키는 객체를 그대로 함께 가리킨다.
따라서, mutable을 받았을 경우에,
새로운 객체를 재할당하려는 것이 아닌 수정만 하려고 하면,
indexing이나 slicing등으로 변경할 수 있는 것이다.
하지만, mutable도 재할당하려면 global을 사용해야한다.
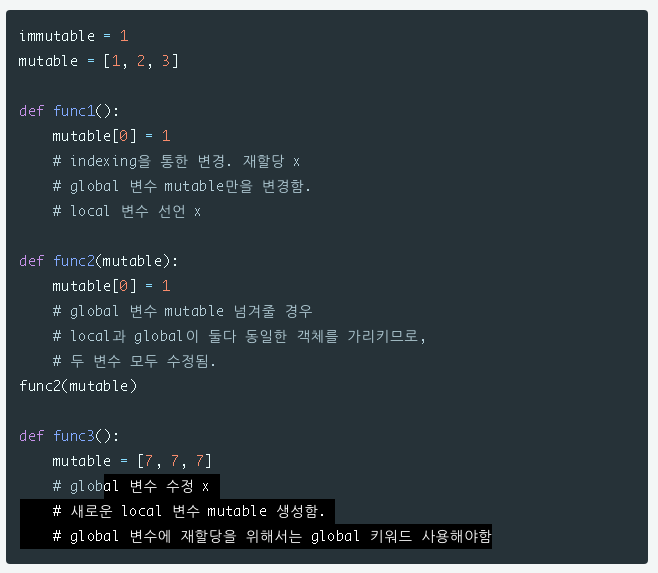
출처 : https://livlikwav.github.io/python/python-mutable-and-namespace/
- 상하좌우를 dfs(x-1,y) 등으로 방문처리를 하였는데 여기서 중요한 부분은 재귀적으로 호출된 dfs의 리턴값들은 상관을 안써도 된다는 것이다.
즉 처음 0에 닿았을때 주변은 다 1로 변하게 된다. 아래의 포문이 돌아가도 원래는 0이었지만 1로 채워진 부분들은 1이기 때문에 건너 뛴다는 것이다. 결국 처음의 0에 대해서만 result += 1이 행해진다.
실전 문제 - 미로 탈출 p.152
책 코드)
from collections import deque
# 입력 받기
n,m = map(int,input().split())
graph = []
for i in range(n):
graph.append(list(map(int,input())))
# 상하좌우 이동 케이스
dx = [-1,1,0,0]
dy = [0,0,-1,1]
# bfs 소스코드 구현
def bfs(x,y):
queue = deque()
queue.append((x,y))
while queue:
x,y = queue.popleft()
# 네 방향 위치 확인
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
#공간 벗어날시
if nx < 0 or ny <0 or nx >= n or ny >= m:
continue
# 벽일때
if graph[nx][ny] == 0:
continue
# 해당 노드를 처음 방문시만 최단 거리 기록
if graph[nx][ny] == 1:
graph[nx][ny] = graph[x][y] + 1
queue.append((nx,ny))
return graph[n-1][m-1]
print(bfs(0,0))
comment) 이 문제를 보고도 ㅋㅋㅋㅋ... 나는 개발자 하기 틀려먹었다.
일단 모든 노드를 탐색하려면 bfs가 효율적이라는 것을 알았다. 그리고 큐라는 무기가 생각보다 강력하였다. 코드를 보면서 논리적으로 이해가 안갔던 부분이 있었다.
바로 최단거리를 어떻게 구할까 였다. 위의 소스코드에서는 1로 되어있는 노드에 대해 각 노드에 대해 최단거리를 다 구할 수 있다. 그 중 탈출구에 있는 값만 리턴을 받기 때문에 탈출구 외의 1에는 관심을 가질 필요가 없다는 것이다. 이러한 문제는 계속 풀어보고 감을 익혀야 될 것 같다.
두 문제를 다시 풀어보았다. queue를 사용할 땐 popleft가 있으면 append도 무조건있다. 맨날 까먹는다 바보라서 ㅋㅋㅋㅋㅋ 그리고 스택을 이용한 dfs일땐 재귀를 써야 간결해진다. 아무튼 백준으로 가보자
복습)
복습 1회
복습 2회
comment)
복습 1회를 마치면서 하 너무 코드를 외우려고만 하는게 아닐까 싶었다. 물론 백준 토마토 문제를 풀때 외웠던 것이 도움이 되긴했지만... 복습할때는 코드를 또 외워서 했다는 느낌이였다. 물론 시간이 부족해서 촉박감에 그런 것일 수도 있겠다 싶었다. 이번 그리디 알고리즘 크게 만들기를 스택으로 푼다는 점을 알고.. 문제를 보고 아 이거 스택으로 풀면 되겠내 라는 생각을 못했다 .... 더 노력하자
복습 2회
comment)
인풋 값이 001010 이렇게 붙어있는데 쪼개서 리스트 넣어야할 때
matrix.append(list(map(int,input())))뒤에 split() 안붙어도 된다.
deque는 x,y 이런식으로는 값을 못받는다. 하나의 argument만 받을 수 있다. 그러므로 x,y라는 좌표를 넣고 싶다면 tuple로 묶어서 넣을 수 있도록 ....

