알고리즘
- 주어진 문제의 해결을 위한 자료구조와 연산방법에 대한 선택
Linear Arrays
선형 배열
index는 0 부터 시작한다
리스트 연산
#원소 추가
list.append('a')
#마지막 원소 추출
list.pop()
- 순식간에 할 수 있는 일
- 리스트의 길이와 무관(상수시간)
시간이 걸리는 작업들은 무엇이 있을까?
list 중간 삽입, 중간 추출
l.insert(index,value)
del(l[2])del과 pop의 차이)
추출된 원소의 유무
위와 같은 연산은 리스트의 길이가 길면 오래 걸리는 일
-> 리스트의 길이에 비례(선형 시간) -> O(n)
리스트 연산
1.원소 탐색하기
l.index('value')
인덱스 반환list 정렬
sorted()
-
내장 함수
정렬된 새로운 리스트 얻어냄 -
내림 차순
reverse = True 옵션
sort()
-
리스트 메서드
해당 리스트 정렬 -
내림 차순
reverse = True 옵션
알파벳 순서가 아닌 문자열 길이로 내가 정렬하고 싶다면?
키를 지정
sorted(l, key=lambda x : len(x))
탐색 알고리즘
선형 탐색
리스트의 길이에 비례하는 시간 소료 -> O(n)
최악의 경우 : 모든 원소를 다 비교해 보아야
이진 탐색 (Bianry Search)
- 탐색하려는 리스트가 이미 정렬되어 있는 경우에만 적용 가능
한 번 비교가 일어날 때마다 리스트 반씩 줄임 (divide & conquer)
-> O(logn)
재귀 알고리즘
하나의 함수에서 자신을 다시 호출하여 작업 처리
재귀 같은 경우는 종료 조건이 필수 이다!(Trivial case)
트리 같은 구조가 효과적
재귀는 while 이나 for 처럼 iterative version이 존재한다.
만약 n이 커지면 어떻게 될까?
n이 커지면 어떻게 될까?
n이 커질 수록 함수 호출 횟수에 비례하기 때문에 둘 다 O(n)
효율성 부분에서 재귀 같은 경우가 떨어진다. 함수 호출이나 부가적인 요소가 더 들어감
#조합의 수 계산 - recursive
def combi(n,m):
if n == m:
return 1
elif m == 0:
return 1
else:
return combi(n-1,m) + combi(n-1,m-1)재귀는 효율이 떨어지긴 하지만 사람이 생각하는 코드를 바로 실행에 옮길 수 있다는 장점
재귀 알고리즘은 인자가 같은 함수 호출을 여러번 반복해야함 -> 효율성이 떨어짐
알고리즘의 복잡도(complexity of Algorithms)
시간복잡도(Time Complexity)
문제의 크기와 이를 해결하는 데 걸리는 시간 사이의 관계
공간복잡도(Space Complexity)
문제의 크기와 이를 해결하는 데 필요한 메모리 공간 사이의 관계
평균 시간 복잡도 (average)
임의의 입력 패턴을 가정했을 때 소요되는 시간의 평균
최악 시간 복잡도(worst - case)
가장 긴 시간을 소요하게 만드는 입력에 따라 소요되는 시간
Big - O Notation
점근 표기법(asymptotic notation)의 하나
어떤 함수의 증가 양상을 다른 함수와의 비교로 표현
(알고리즘의 복잡도를 표현할 때 흔히 쓰임)
수학적인 정의는 일단 차치하고
입력의 크기가 n 일 때,
ex) O(logn) - 입력의 크기의 로그에 비례하는 시간 소요
(계수는 그다지 중요하지 않음)
선형 시간 알고리즘
만약 최댓값을 찾는 다는 가정이라면 - 끝까지 다 살펴 보기 전까지는 알 수 없음
Average case, Worst-case 둘 다 O(n) 인 듯
로그 시간 알고리즘
ex) n 개의 크기 순으로 정렬된 수에서 특정 값을 찾기 위해 이진 탐색 알고리즘을 적용
이차 시간 알고리즘 - O(n^2)
삽입 정렬
하나의 원소를 집어 넣을 때 n에 비례하는 원소 중 위치를 찾고, n 만큼 원소를 넣어야하기 때문에
best case : O(n) -> 정렬되어 있을 때
worst case : O(n^2) -> 역순 원래는 /2 이지만 계수는 중시하지 않음
보다 나은(낮은) 복잡도를 가지는 정렬 알고리즘은 없는가?
있다, 병합 정렬
(merge sort) - O(nlogn)
참고 : 입력 패턴에 따라 정렬 속도에 차이가 있지만 정렬 문제에 대해 nlogn 보다 낮은 복잡도를 갖는 알고리즘은 존재할 수 없음이 증명되어 있음
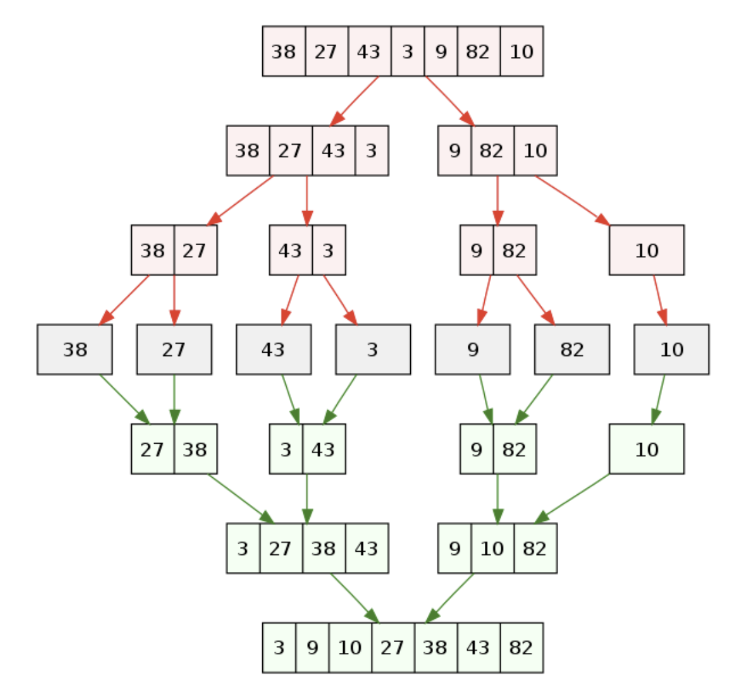
정렬할 데이터를 반씩 나누어 각각을 정렬시킨다. 정렬된 데이터를 두 묶음씩 한데 합친다.
복잡한 문제
- 유명한 예: 배낭 문제 (Knapsack Problem)`

