1. 고민의 시작
백준 알고리즘 9663번 문제인 N-Queen은 백트래킹 알고리즘으로 풀어야 하고 대표적으로 나오는 문제 중 하나입니다. 제한 시간 10초나 줘서 처음엔 널널하네~ 라는 생각이 들면서 풀다 보면 아니라는 걸 깨닫게 되었죠. 😥
규칙은 간단합니다! N을 입력 받고 N x N 개의 체스판에서 N개의 퀸 체스 말을 겹치지 않고 놓을 수 있는 경우의 수를 출력하면 됩니다. 퀸은 일직선이나 대각선으로 이동할 수 있으며 서로 공격할 수 있는 곳에 놓을 수 없습니다.
우선 백트래킹은 경우의 수가 그려진 아래의 사진처럼 모든 케이스를 탐색하며 돌아야 하는데, 그중 안되는 경우는 미리 정리하고 되는 곳은 끝까지 탐색하는 기법입니다. 경우의 수를 잘 걸러서 더 깊이 탐색하지 않도록 효율적으로 체크하는 것이 중요합니다.

2. 알고리즘 구상
백준 알고리즘 9663번 문제인 N-Queen에서 최대 입력값으로 15가 주어지게 되는데 모든 경우의 수를 탐색하면 15의 15제곱 만큼 탐색해야 할 수도 있습니다... 그렇기에 중간에 체크하는 과정을 넣어야 하고 이것은 규칙에서 주어진 내용을 활용하여 적용하면 되겠다고 생각했습니다.
한 열에는 하나의 퀸만 올 수 있으니 한 줄에 놓을 수 있는 케이스를 반복하고 놓을 수 있는 곳에는 다시 재귀 호출을 통해 최종 깊이인 N만큼 탐색할 수 있도록 하는 DFS(깊이우선탐색)을 사용했습니다. 그 자리에 놓을 수 있는지 체크하는 함수는 이전 라인들을 반복 탐색하면서 이미 1이 있는지 없는지를 확인하여 결과를 반환할 수 있도록 구상 해보았습니다.
3. 문제의 연속
3.1 변수 선언의 문제
변경전 코드
table = [[0] * table_length] * table_length 변경 후 코드
for i in range(table_length):
table.append([0] * table_length)
dic[i] = 0알고리즘이랑 체크하는 부분을 모두 구현하고 돌려보는데 돌아가지 않았습니다 ㅠㅠ 로직을 뜯어봐도 아무런 문제가 없었는데 반복이 이상하게 돌아가고 중간에 테스트하는 코드를 끼워넣어서 확인해봐도 처음보는 문제였습니다. 결국 모든 코드를 한줄 한줄 보았는데 결국 이 부분이 문제였습니다. 5시간 넘게 이거 때문에 싸우고 있었던 걸 생각하니 허무했죠.
table[0][0] = 1 을 넣었을 때 모든 줄의 0번째 자리가 1로 바뀌는걸 발견하고 테이블의 모든 라인을 반복문으로 선언을 통해 만들어지게 해서 해결하였습니다.
C언어에서는 모든 참조 변수는 메모리를 직접 할당하여 사용하다 보니 확실하게 할 수 있었는데 파이썬의 경우 지식 부족으로 알아서 다 할당하겠지~ 했던게 원인이였습니다. 이후 파이썬 문법과 깊은 복사, 얕은 복사에 대해 공부하여 원인과 이유에 대해 확실하게 알 수 있었습니다.
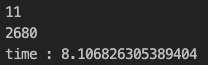
3.2 시간 복잡도의 문제
개선 전 시간
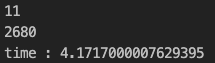
개선 후 시간
무려 2배나 빨라졌습니다!! 😧
제 N-Queen 알고리즘은 한 줄에 하나의 퀸만 놓을 수 있다는 걸 생각해서 한 줄에 올 수 있는 경우의 수를 반복하고 다음 줄로 재귀 호출하여 또 반복시키는 깊이 우선 탐색으로 되어 있습니다.
그렇기에 그 자리에 놓을 수 있는지 체크하는 부분이 중요했는데 제 코드에선 이전 라인들을 반복을 통해 겹치는 곳이 있는지 체크 하다보니 시간적인 문제가 발생했습니다. 만약 5 번째 줄에서 해당 자리에 놓을지 체크를 하려면 1~4 번 줄을 반복문으로 확인해야 했었죠.
해결방법으로 딕셔너리를 사용하여 변수를 만들고 퀸을 놓으면서 딕셔너리 변수에 미리 표시하였고 해당 줄에 놓을지 말지는 이를 활용하여 반복을 거치지 않고도 바로 확인을 할 수 있게 했습니다.
개선 전에는 백준에서 Python3는 물론이고 PyPy3으로 제출해도 시간 초과 났던 부분이, 개선 후에는 PyPy3에서 통과할 수 있게 되었습니다!
4. 제출
코드의 가독성의 부분에 있어서 괜찮게 코드를 짰다고 생각이 되었지만 시간적인 부분에 있어서는 여전히 아쉬움이 남았습니다. 동료가 만든 N-Queen을 코드 리뷰하였는데 배울만한 점이 많았고 참신한 점도 있었습니다.
제 알고리즘에선 해당 자리를 놓기 위해 일일이 체크해야 했다면, 반대로 동료의 코드에선 먼저 놓을 수 없는 곳을 체크를 시켜 시간 복잡도를 줄인 것을 보았습니다. 실제로 실행 시간도 조금 더 빨랐고 입력되는 N이 커질 수록 차이가 커졌습니다.
백트래킹 기법에 대해 조금 더 자세히 이해할 수 있게 된 문제였고 비슷한 문제라면 금방 풀 수 있을 것 같습니다. 마지막으로 제출한 코드로 글을 마무리하겠습니다. 😃
# 백준 9663 N-Queen
import time
start = time.time()
def queen(table, n, table_length):
global count
for i in range(table_length): # 한 열에 놓을 수 있는 케이스
if check(table, n, i, table_length) == True: # 놓을 수 있다면
if n == table_length - 1: # 열의 마지막에 도착했다면
count += 1 # 카운트 +1하고 반복 break
break
table[n][i] = 1 # 테이블에 퀸 놓고 아래에서 재귀 탐색
dic[i] = 1 # 해당 열에 놓았다고 표시하기
queen(table, n + 1, table_length)
table[n][i] = 0 # 재귀 탐색이 끝났으므로 원래대로
dic[i] = 0 # 열에 놓았다는 표시 지우기
# 테이블 체크 함수
def check(table, n, now, table_length):
n -= 1 # 이전 줄부터 검사
if dic[now] == 1: # 같은 라인에 이미 값이 있는지
return False
side = 1 # 대각선으로 체크하기 위한 변수
while 0 <= n: # n-1번째부터 0번째까지 체크
if (now - side) >= 0 and table[n][now-side] == 1: # 대각선으로 앞쪽
return False
if (now + side) < table_length and table[n][now+side] == 1: #대각선으로 뒷쪽
return False
n -= 1 # 이전 줄로
side += 1 # 더 대각선으로
return True
# 시작
global count
count = 0
table_length = int(input())
# table = [[0] * table_length] * table_length # 엄청난 실수
table = list()
dic = {}
for i in range(table_length):
table.append([0] * table_length)
dic[i] = 0
queen(table, 0, table_length)
print(count)
print("time :", time.time() - start)