개요
개요
https://www.youtube.com/playlist?list=PLFt_AvWsXl0cq5Umv3pMC9SPnKjfp9eGW
위의 재생목록 링크를 통해 유니티에서 A* 알고리즘을 공부하며 정리하는 글이다.
4번째 영상을 보고 정리한 글이다.
지금까지 구현한 알고리즘에 자료구조 Heap을 이용해 최적화를 한다. (min heap을 이용)
특이사항으로는 priority_queue를 사용하지 않고, Heap자료구조를 직접 구현했다.
이해를 돕기위함인 것 같다.
예전에 C++로 한번 구현을 해봤어서 어렵지 않게 따라갈 수 있었다.
[C++로 Heap구현 ]
Heap 클래스와 IHeapItem인터페이스
generic형을 사용해 구현했다.
우리는 타입 T로 Node를 사용한다.
heap클래스에서 노드끼리 비교할때는 fcost(같을 경우 hcost)를 기준으로 비교한다.
IHeapItem인터페이스
public interface IHeapItem<T> : IComparable<T>
{
int heapIndex
{
get;
set;
}
}IheapItem들은 공통적으로 heapIndex를 가지고 있으며,
Heap클래스의 T[] items; 배열을 이용해 관리한다.
Heap클래스 :: Add함수
public void Add(T item)
{
item.heapIndex = currentItemCount;
items[currentItemCount++] = item;
SortUp(item);
}currentItemCount는 현재 heap에서 마지막 원소 다음 인덱스를 가리키는 변수다.
Heap에 새로운 아이템이 추가되면 마지막 원소로 넣어준 후, currentItemCount를 증가시켜준다.
그 후, SortUp함수를 이용해 해당 Item을 parent값과 비교하면서 자기자리를 찾아가게한다.
Heap클래스 :: RemoveFirst함수
public T RemoveFirst()
{
T firstItem = items[0];
items[0] = items[--currentItemCount];
items[0].heapIndex = 0;
SortDown(items[0]);
return firstItem;
} 첫번째 값 (minHeap을 구현하므로 제일 작은 값이다.) 을 반환한다.
맨 마지막 원소를 0번 인덱스에 넣은 다음, 해당 원소를 자식들과 비교하며 제자리를 찾아가게 하는 SortDown함수를 호출한다.
Heap클래스 :: Count함수
public int Count
{
get
{
return currentItemCount;
}
}count함수는 currentItemCount값을 반환하는 방식으로 현재 heap의 원소가 몇개인지 반환하는 함수다.
Heap클래스 :: Contains함수
public bool Contains(T item)
{
return Equals(items[item.heapIndex],item);
} 인자로 들어온 item인자가 items배열에 존재하는지 bool형으로 반환하는 함수다.
방법은 item의 heapIndex 값을 인덱스로 가지는 items 배열의 원소를 조사해 같은지 확인한다.
Heap클래스 :: SortDown함수
public void SortDown(T item)
{
while (true) {
int leftChildIndex = item.heapIndex * 2 + 1;
int rightChildIndex = item.heapIndex * 2 + 2;
int swapIndex = 0;
if (leftChildIndex < currentItemCount)
{
//자식 중 더 작은 자식노드 찾는 방식
swapIndex = leftChildIndex;
if(rightChildIndex<currentItemCount)
if (items[swapIndex].CompareTo(items[rightChildIndex]) > 0)
{
swapIndex = rightChildIndex;
}
if (item.CompareTo(items[swapIndex]) > 0)
{
Swap(item, items[swapIndex]);
}
else
{
return;
}
}
else
return;
}
} 인자로 들어온 item 을 자식노드들의 heapindex와 비교하며 제자리를 찾아가는 함수다.
자식값은 현재 인덱스 * 2 + 1 , 현재 인덱스 * 2+2 로 표현할 수 있다.
먼저 왼쪽 자식과 오른쪽 자식이 범위를 넘어가는지 체크하고 , 둘 중에 더 작은 값을 찾는다.
더 작은 값과 item을 비교해 item이 더 크다면 swap한다.
item이 두 자식값보다 작을 때까지 반복한다.
Heap클래스:: SortUp함수
public void SortUp(T item)
{
//heap에서 부모 노드의 인덱스는 인덱스-1 /2 이다.
int parentIndex = (item.heapIndex - 1) / 2;
while(true)
{
T parentItem = items[parentIndex];
if (item.CompareTo(parentItem) < 0)
{
Swap(item, parentItem);
}
else
break;
parentIndex = (item.heapIndex - 1) / 2;
}
} heap에서 부모의 인덱스는 (자식의 인덱스 - 1) / 2 이다.
인자로 들어온 item의 부모노드의 값과 비교한다.
부모노드보다 item의 값이 작다면 서로 스왑한다.
부모노드보다 item값이 클때까지 반복해준다.
Heap클래스 :: swap함수
public void Swap(T itemA, T itemB)
{
items[itemA.heapIndex] = itemB;
items[itemB.heapIndex]= itemA;
int tmpIndex = itemA.heapIndex;
itemA.heapIndex = itemB.heapIndex;
itemB.heapIndex = tmpIndex;
} swap함수에서는 items배열에서 서로의 아이템 인덱스를 바꿔준 후,
서로 아이템의 heapIndex값까지 변경해줘야한다.
Heap클래스 전체 코드
public class Heap<T> where T : IHeapItem<T>
{
T[] items;
int currentItemCount;
public Heap(int maxCountSize)
{
items = new T[maxCountSize];
}
public void Add(T item)
{
item.heapIndex = currentItemCount;
items[currentItemCount++] = item;
SortUp(item);
}
public T RemoveFirst()
{
T firstItem = items[0];
items[0] = items[--currentItemCount];
items[0].heapIndex = 0;
SortDown(items[0]);
return firstItem;
}
public void UpdateItem(T item)
{
SortUp(item);
}
public int Count
{
get
{
return currentItemCount;
}
}
public bool Contains(T item)
{
return Equals(items[item.heapIndex],item);
}
public void SortDown(T item)
{
while (true) {
int leftChildIndex = item.heapIndex * 2 + 1;
int rightChildIndex = item.heapIndex * 2 + 2;
int swapIndex = 0;
if (leftChildIndex < currentItemCount)
{
//자식 중 더 작은 자식노드 찾는 방식
swapIndex = leftChildIndex;
if(rightChildIndex<currentItemCount)
if (items[swapIndex].CompareTo(items[rightChildIndex]) > 0)
{
swapIndex = rightChildIndex;
}
if (item.CompareTo(items[swapIndex]) > 0)
{
Swap(item, items[swapIndex]);
}
else
{
return;
}
}
else
return;
}
}
public void SortUp(T item)
{
//heap에서 부모 노드의 인덱스는 인덱스-1 /2 이다.
int parentIndex = (item.heapIndex - 1) / 2;
while(true)
{
T parentItem = items[parentIndex];
if (item.CompareTo(parentItem) < 0)
{
Swap(item, parentItem);
}
else
break;
parentIndex = (item.heapIndex - 1) / 2;
}
}
public void Swap(T itemA, T itemB)
{
items[itemA.heapIndex] = itemB;
items[itemB.heapIndex]= itemA;
int tmpIndex = itemA.heapIndex;
itemA.heapIndex = itemB.heapIndex;
itemB.heapIndex = tmpIndex;
}
}Node클래스 추가
Heap클래스에서 사용할수 있도록 IHeapItem인터페이스를 상속받아야한다.
heapIndex를 추가해주고, IHeapItem이 IComparable을 상속 받으므로,
CompareTo도 작성해줘야한다.
public class Node:IHeapItem<Node>{
//추가된 부분
public int heapIndex { get; set; }
public int CompareTo(Node nodeToCompare)
{
int compare = fCost.CompareTo(nodeToCompare.fCost);
//FCost가 같다면
if (compare == 0)
{
compare = hCost.CompareTo(nodeToCompare.hCost);
}
return compare;
}
} CompareTo함수를 보면 fcost를 기준으로 먼저 비교하고,
fCost가 같다면 hCost를 기준으로 비교한다.
Agrid클래스 추가
heap클래스에서 전체 gird 크기를 알 수 있어야하므로 MaxSize를 반환하는 함수를 추가했다.
public int MaxSize
{
get {
return gridXCnt * gridYCnt;
}
} 또한 지나갈 수 없는 벽들이랑 그라운드를 이제 굳이 구분 안해도 된다.
경로만 볼 수 있도록, bool형 변수 onlyDisplayPathGizmos 를 선언했다.
private void OnDrawGizmos()
{
Gizmos.DrawWireCube(transform.position, new Vector3(gridWorldSize.x, 1, gridWorldSize.y));
if (onlyDisplayPathGizmos)
{
if (path != null)
{
foreach (Node n in path)
{
Gizmos.color = Color.black;
Gizmos.DrawCube(n.worldPosition, Vector3.one * (nodeDiameter - .1f));
}
}
}
else
{
if (grid != null)
{
Node playerNode = GetNodeFromWorldPoint(player.transform.position);
foreach (Node n in grid)
{
Gizmos.color = (n.walkable) ? Color.green : Color.red;
//if (playerNode == n) Gizmos.color = Color.cyan;
if (path.Contains(n))
{
Gizmos.color = Color.black;
}
Gizmos.DrawCube(n.worldPosition, Vector3.one * (nodeDiameter - .1f));
}
}
}
} 이렇게 onlyDisplayPathGizmos변수가 true로 설정되어있다면
경로만 그리도록 빼줬다.
PathFinding함수 추가
List로 선언되어있던 openSet을 우리가 구현한 Heap으로 변경해준 후,
agrid.MaxSize로 크기를 선언해준다.
Heap<Node> openSet = new Heap<Node>(agrid.MaxSize);Heap을 사용하는 방식으로 바꿨으니 FindPath함수도 변경해야 한다.
//open Set에서 fcost가 제일작은 값을 찾아 curNode 에 넣음, fcost가 같을땐 hcost가 더 작은 값을 고름
Node curNode = openSet[0];
for(int i = 1; i < openSet.Count; i++)
{
if (openSet[i].fCost< curNode.fCost || (openSet[i].fCost==curNode.fCost && openSet[i].hCost < curNode.hCost))
{
curNode = openSet[i];
}
}
openSet.Remove(curNode);원래 선언되어있던 위 코드를 아래처럼 간단하게 변경할 수 있게되었다.
Node curNode = openSet.RemoveFirst();이웃 노드들을 순회할때 이제 List가 아니라 Heap구조에 넣어야한다.
또한, A* 알고리즘 내부에서 새로운 노드의 GCost를 변경해야할때,
openSet에 이미 포함된 친구라면 UpdateItem함수를 호출해야한다.
이렇게 해야 SortUp함수가 호출되며 제자리를 찾아간다.
if (newGCost < elem.gCost || !openSet.Contains(elem))
{
elem.gCost = newGCost;
elem.hCost = GetDistance(elem, targetNode);
elem.Parent = curNode;
if (!openSet.Contains(elem))
{
openSet.Add(elem);
}
else
openSet.UpdateItem(elem);
}후술할 내용인 stopwatch도 시간을 재기 위해 넣었다.
함수 시작할때 start를 해주고,
private void FindPath(Vector3 startPos, Vector3 targetPos)
{
Stopwatch sw= new Stopwatch();
sw.Start();해당 노드를 찾았을 때, Stop을 하고 시간을 콘솔창에 띄워봤다.
if (curNode == targetNode)
{
sw.Stop();
UnityEngine.Debug.Log("path found " + sw.ElapsedMilliseconds+"ms");
RetracePath(startNode, targetNode) ;
return;
}실행 예
영상을 보며 배운 기술인데, System.Diagnostics 네임스페이스를 선언해주면
stopwatch를 사용할 수가 있다.
Stopwatch sw= new Stopwatch();
sw.Start();이렇게 시작을 하고,
sw.Stop();
UnityEngine.Debug.Log("path found " + sw.ElapsedMilliseconds+"ms"); 이렇게 Stop함수로 멈춘 다음, sw.ElapsedMilliseconds를 이용해
로그를 찍어준다.
스탑워치를 이용해 heap으로 최적화하기 전과 한 후 시간을 비교해봤다.
비교를 더 쉽게 하기위해 노드는 x축으로 300개 y축으로 300개 총 9만개를 잡았다.
-
list를 순회하며 제일 작은 노드 탐색(저번 구현)
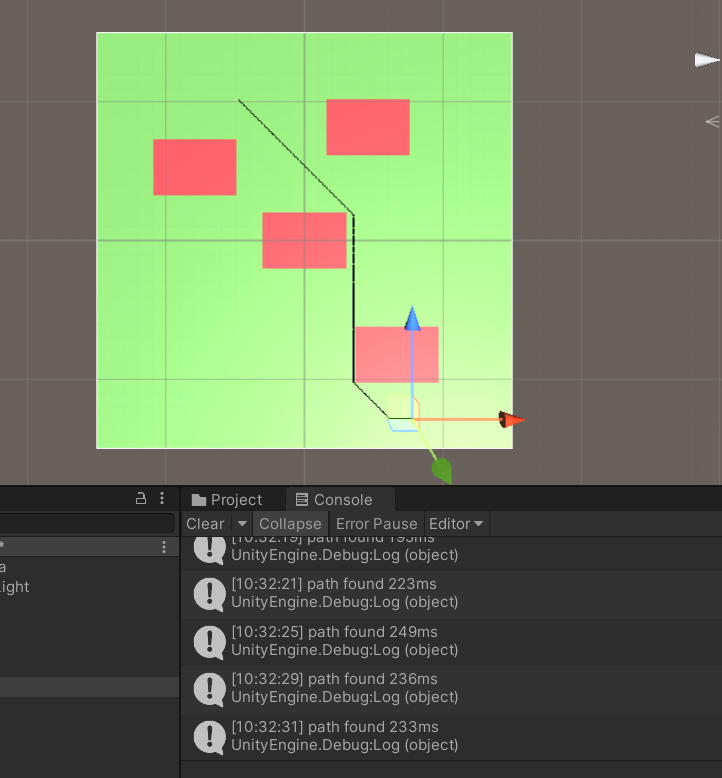
223~ 249ms까지 나온다. -
Heap을 이용하여 제일 작은 노드 탐색(이번 구현)
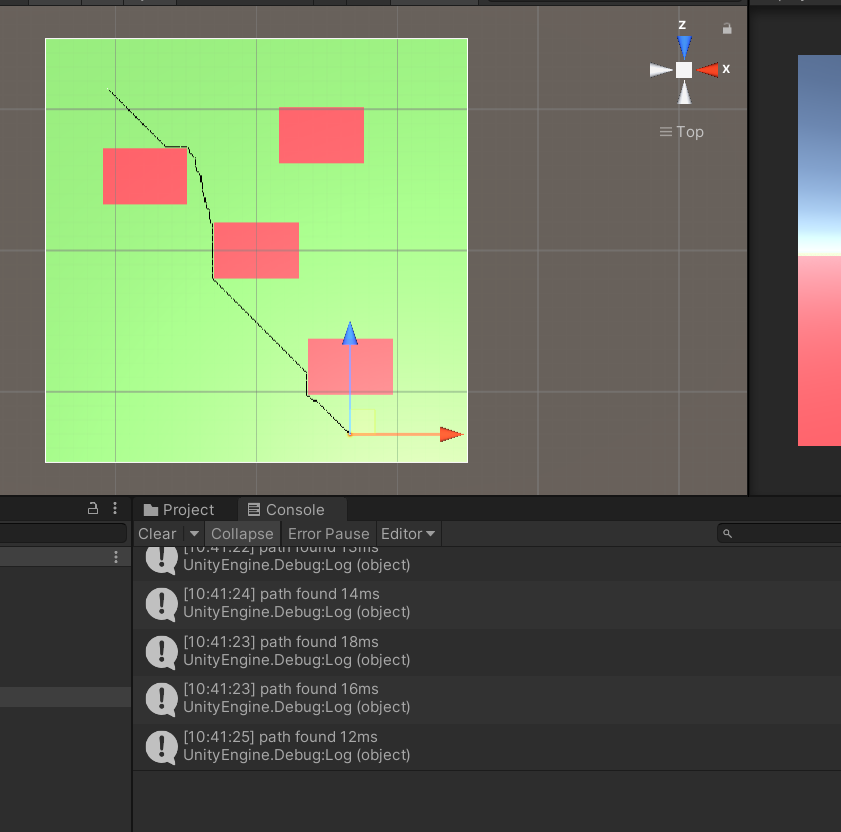
12~ 18ms가 나온다.최소값 탐색 제외하고 나머지 연산들이 있기에
정확히 log2(N)을 따라가진 않지만 그래도 효과적으로 줄었다.
생각
아,, Heap을 구현하는데 뭘 잘못 썼는지 계속 무한루프에 걸려서
해결하는데 시간이 많이 들어갔다.
결국 모든 반복문에 int detector 변수 선언해주고,
while(detector++>10000) throw new system.exception 을 넣어서야
간신히 캐치했다..
놀랍게도 Swap함수에서 heapIndex 스왑할 때,
int tmpIndex = itemA.heapIndex;
itemA.heapIndex = itemB.heapIndex;
itemA.heapIndex = tmpIndex;이런 식으로 스왑해버려서 B가 바뀌질 않았다! 매우 화가 났다.
너무 구현이 간단한 부분이라 저 함수는 쳐다보지도않고 나머지 함수들만
냅다 들여다 본게 문제였다.
생각해보니 Heap에서 무한루프가 걸리는 부분이라 해봐야
비교함수 잘 작동하는지랑 Swap잘 작동하는지 이 두 개일텐데 흠..
좋은 교훈을 얻었다.. 더 신중해지자,
